3. Компоненты временных рядов
Ряд динамики может быть подвержен влиянию факторов эволюционного и осциллятивного характера, а также находиться под влиянием факторов разного, как правило, случайного воздействия.
1) Влияние эволюционного характера - это изменения, определяющие общее направление развития, как бы многолетнюю эволюцию, которая пробивает себе дорогу через другие систематические и случайные колебания.
Такие изменения динамического ряда называются тенденцией развития или трендом.
2) Влияние осциллятивного характера - это циклические (конъюнктурные) и сезонные колебания.
Циклические колебания можно представить в виде синусоиды y =sin(t) (значение признака вначале возрастает, достигает определенного max, затем снижается, достигает своего min, вновь возрастает и т.д.).
Циклические колебания в экономических расчетах примерно соответствуют так называемым циклам конъюнктуры.7
Сезонные колебания - это колебания, периодически повторяющиеся в некоторое определенное время каждого года, дня месяца или часа дня. Эти изменения отчетливо наблюдаются на графиках многих рядов динамики, содержащих данные за период не менее одного года.
Последней группой факторов, влияющих на ряд динамики являются факторы, вызывающие нерегулярные колебания уровней. Эти факторы подразделяются в свою очередь на:
• вызывающие спорадические изменения уровней (война, экологические катастрофы, эпидемии и т.д.),
• случайные, слабо воздействующие, второстепенные факторы вызывающие случайные разнонаправленные изменения уровней.
Таким образом, уровни ряда динамики подвержены разным воздействиям, и теоретически ряд динамики может быть представлен как функция следующих компонент:
y = f (T,R,S,Е), где
Т – тренд;
R – циклические колебания;
S - сезонные колебания;
Е – случайные колебания.
Так как каждый фактор вызывает повышение или понижение уровней, то каждую компоненту и исходный динамический ряд можно представить в векторной форме:
yr = f (Tr ,Rr ,Sr, еr) .
В зависимости от связи компонент между собой можно построить две модели ряда динамики:
- аддитивная модель: yr =Tr +Rr +Sr +еr - характеризуется тем, что характер циклических и сезонных колебаний остается постоянными,
- мультипликативная модель: yr =Tr *Rr *Sr *еr - если характер циклических и сезонных колебаний остается постоянным только по отношению к тренду.
4. Методы измерения параметров тренда
Тенденция ряда динамики (тренд). Важнейшим направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда).8
Основная тенденция (тренд) – достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайный колебаний. Основную тенденцию можно представить либо аналитически – в виде уравнения (модели) тренда, либо графически.
Изучение тренда включает в себя два этапа:
1. Проверка ряда на наличие тренда;
2. Выравнивание ряда динамики и непосредственное выделение тренда.
Начальным этапом выделения и анализа тренда является проверка гипотезы о существовании тренда.
Существует около десятка критериев проверки наличия тренда. Рассмотрим некоторые из них.
1. Проверка существенности разности средних. Ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разности средних : Н0: у1 = у2 . Так как число членов анализируемого ряда, как правило, мало, то для проверки гипотезы воспользуемся теорий малой выборки. За основу проверки берется tб - критерий Стьюдента. При t ≥ tб гипотеза об отсутствии тренда отвергается и наоборот при t < или = tб гипотеза (Н0) принимается. Здесь t - расчетное значение, найденное для анализируемых данных. tб - табличное значение критерия при уровне вероятности ошибки, равном б. В случае равенства или при несущественном различии дисперсий двух исследуемых совокупностей (у12 =у22 ) определение расчетного значения t производится по зависимости
,
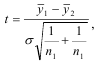Где у1 и у2 средние для первой и второй половины ряда динамики;
n1 и n2 - число наблюдений в этих рядах;9
у - среднеквадратическое отклонение разности средних, определяемое по зависимости
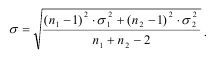
Дисперсии для первой и второй частей ряда рассчитываются по зависимости
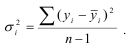
Проверка гипотезы о равенстве дисперсий осуществляется с помощью F -критерия, основанного на сравнении расчетного отношения с табличным. Расчетное значение критерия определяется по формуле
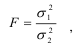
Если расчетное значение F меньше табличного, при заданном уровне значимости то гипотеза о равенстве дисперсий принимается.
Если F больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется и зависимость для расчета t не пригодна для использования.
При выполнении условия о равенстве дисперсий, определяется значение tб и проверяется гипотеза (Н0). При этом теоретическое значение tб определяется с числом степеней свободы равным n1 + n2 -2
Рассмотренный метод дает положительные результаты для рядов с монотонной тенденцией. Когда же ряд динамики меняет общее направление развития, то точка поворота тенденции оказывается близкой к середине ряда. Поэтому средние двух отрезков будут близки, а проверка может не показать наличие тенденции.
2. Второй метод проверки наличия тенденции называется методом
Фостера-Стьюарта, который помимо определения наличия тенденции позволяет обнаружить тренд дисперсии уровней ряда динамики, что важно знать при анализе и прогнозировании экономических явлений.10
После установления наличия тенденции в ряду динамики, производится ее описание с помощью методов сглаживания. К этим методам относятся:
1. Метод укрупнения интервалов является одним из наиболее простых методов непосредственного выявления основной тенденции. При использовании этого метода ряд динамики, состоящий из мелких интервалов, заменяется рядом, состоящим из более крупных интервалов.
Так как на каждый уровень исходного ряда влияют факторы, вызывающие их разнонаправленное изменение, то это мешает видеть основную тенденцию. При укрупнении интервалов влияние факторов нивелируется, и основная тенденция проявляется более отчетливо. Расчет среднего значения уровня по укрупненному интервалу осуществляется по формуле простой средней арифметической.
Недостатком этого способа является то, что сокращается число уровней ряда, а это не позволяет учитывать изменения внутри укрупненного интервала. К его преимуществам можно отнести сохранение природы явления.
Исходный ряд не показывает последовательного роста или снижения объемов выпуска. Изменение уровней не имеет общего направления, они то растут, то снижаются. Заменим месячные интервалы квартальными, соответственно изменив и уровни показателя. Для этого рассчитаем среднемесячные уровни по данным кварталов. Новый ряд состоит из 4-х уровней, каждый из которых является среднемесячным объемом выпуска, рассчитанным по данным соответствующего квартала. В полученном ряду отчетливо просматривается последовательный рост объемов производства в течение года.11
2. Метод простой скользящей средней. Заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т. д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий. Отсюда название – скользящая средняя.
3. Метод взвешенной скользящей средней. Основное отличие от предыдущего метода состоит в том, что уровни, входящие в интервал усреднения суммируются с различными весами, так как аппроксимация в пределах интервала сглаживания осуществляется с использованием уровней, рассчитанных по полиному n –го порядка
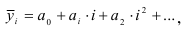
где i - порядковый номер уровня интервала сглаживания.