Лекции по ТОЭ3 / Лекция №8 25.10.2003

Created by SuhOFFF

Рассмотрим соединение типа «звезда-треугольник».

Ток вызван напряжением между точками и , поэтому его можно найти по следующей формуле: .

Аналогично можно найти токи и , которые вызваны напряжениями между точками и и точками и , соответственно, поэтому их можно найти по следующим формулам: и .

Линейные токи определяются через фазовые токи по первому закону Кирхгофа, то есть: ; ; .

Рассмотрим случай равномерной нагрузки, то есть .

В этом случае токи можно найти по следующим формулам: , , . Так нагрузка равномерная, то модули этих токов будут равны, то есть:.

При равномерной нагрузке фаз линейные токи по модулю в раз больше фазовых токов нагрузки, то есть:

;

;

.

Если нагрузка равномерная, то линейное напряжение равно фазовому (), а линейный ток больше в раз фазового ().

Рассмотрим случай неравномерной нагрузки.

;

;

;

;

;

;

;

.

Линейные напряжения:

;

;

.

Ф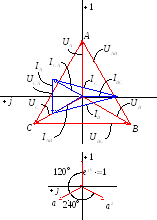азовые токи:

;

;

.

Линейные токи:

;

;

.

Комплексное число по модулю равно единице. Обозначим это комплексное число за - оператор трёхфазной цепи. Тогда: , а , .

Схема типа «звезда-звезда» без нулевого провода.

Такая схема решается с помощью метода двух узлов.

.

Токи в ветвях определяются с помощью законов Ома:

;

;

.

Если нагрузка равномерная, то есть , то: , тогда: , , .

Пример:

Рассмотрим схему типа «звезда-звезда», у которой , , , тогда: ;

;

;

;

.

Электротехника и электроника