4. Упругие и механические свойства твердых тел

Механические свойства твердого тела отражают его реакцию на воздействие внешних силовых факторов (сжатие, растяжение, изгиб, удар, кручение и т.п.). Механические свойства определяются, в первую очередь, силами связи между атомами и молекулами твердого тела, а также точечными дефектами и дислокациями.

4.1. Механическое напряжение и деформация

Под действием внешних сил в каждой точке твердого тела возникают механические напряжения.

Механическое напряжение численно равно силе, действующей на единицу площади.

Растянем силой цилиндр площадью S (рис. 4.1)

 (4.1)

Размерность || = 1 Н/м² = 1 Па (как и давление).

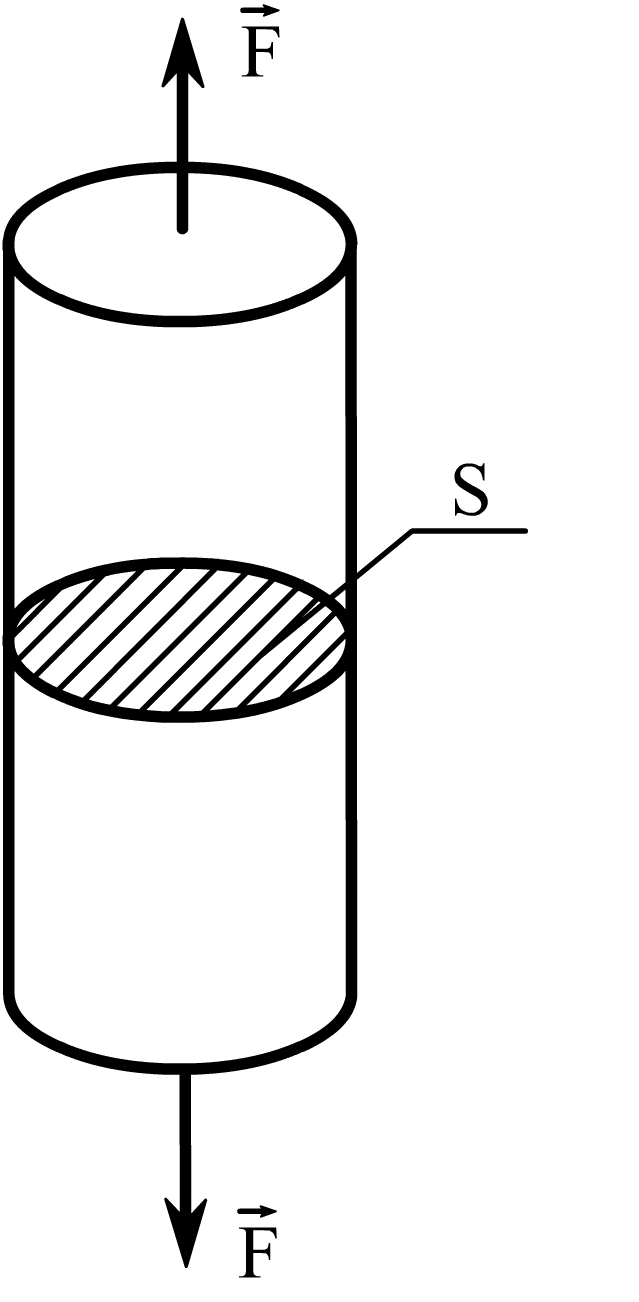
Рис. 4.1. К определению понятия механических напряжений

Это условное напряжение без учета деформации сечения S образца, в формуле (4.1) S – первоначальное сечение.

Истинное напряжение учитывает изменение площади S сечения образца под действием силы (рис. 4.2).

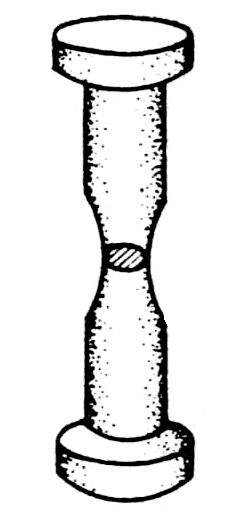
Рис. 4.2. Реальный образец при деформации меняет поперечное сечение

В трехмерном случае вводится тензор напряжений (рис. 4.3) Т_:

(4.2)

_ij = _ji , и в главных осях _ij = 0 (i  j).

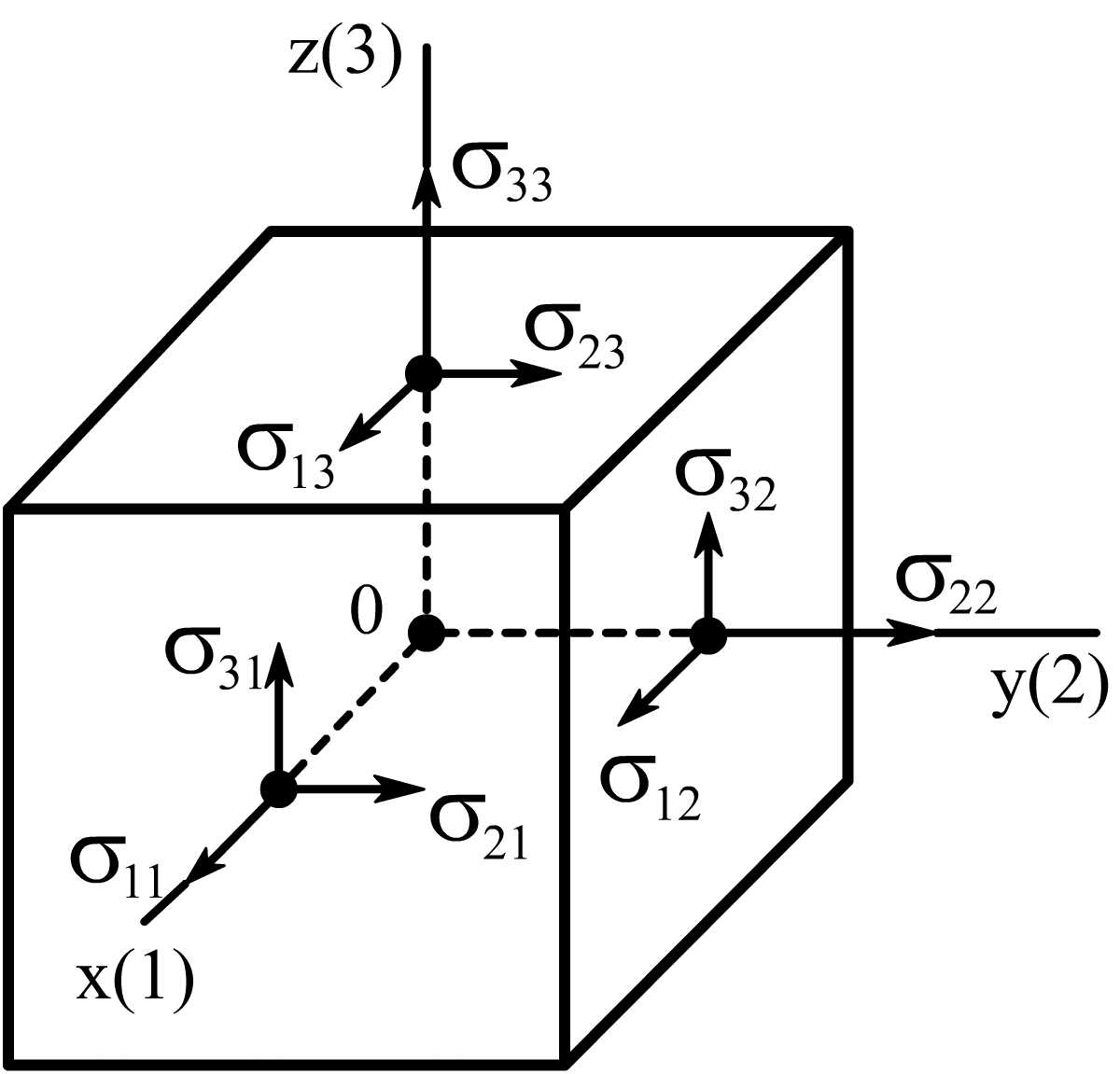
Рис. 4.3. Компоненты тензора напряжений в кубе

Касательные напряжения _ij определяют пластическую деформацию, а нормальные _ii – способствуют разрыву межатомных связей, т.е. хрупкому разрушению твердого тела.

Коэффициент “мягкости” равен _ij/_ii. Чем меньше коэффициент мягкости, тем “жестче” напряженное состояние.

Деформация – это изменение формы или объема твердого тела без изменения его массы под действием внешней силы. При деформации меняется расстояние между какими-либо точками твердого тела. Виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб.

При растяжении (рис. 4.4) относительная деформация исходного образца длиной l_o (в процентах):

, (4.3)

где l_k – конечная длина образца.

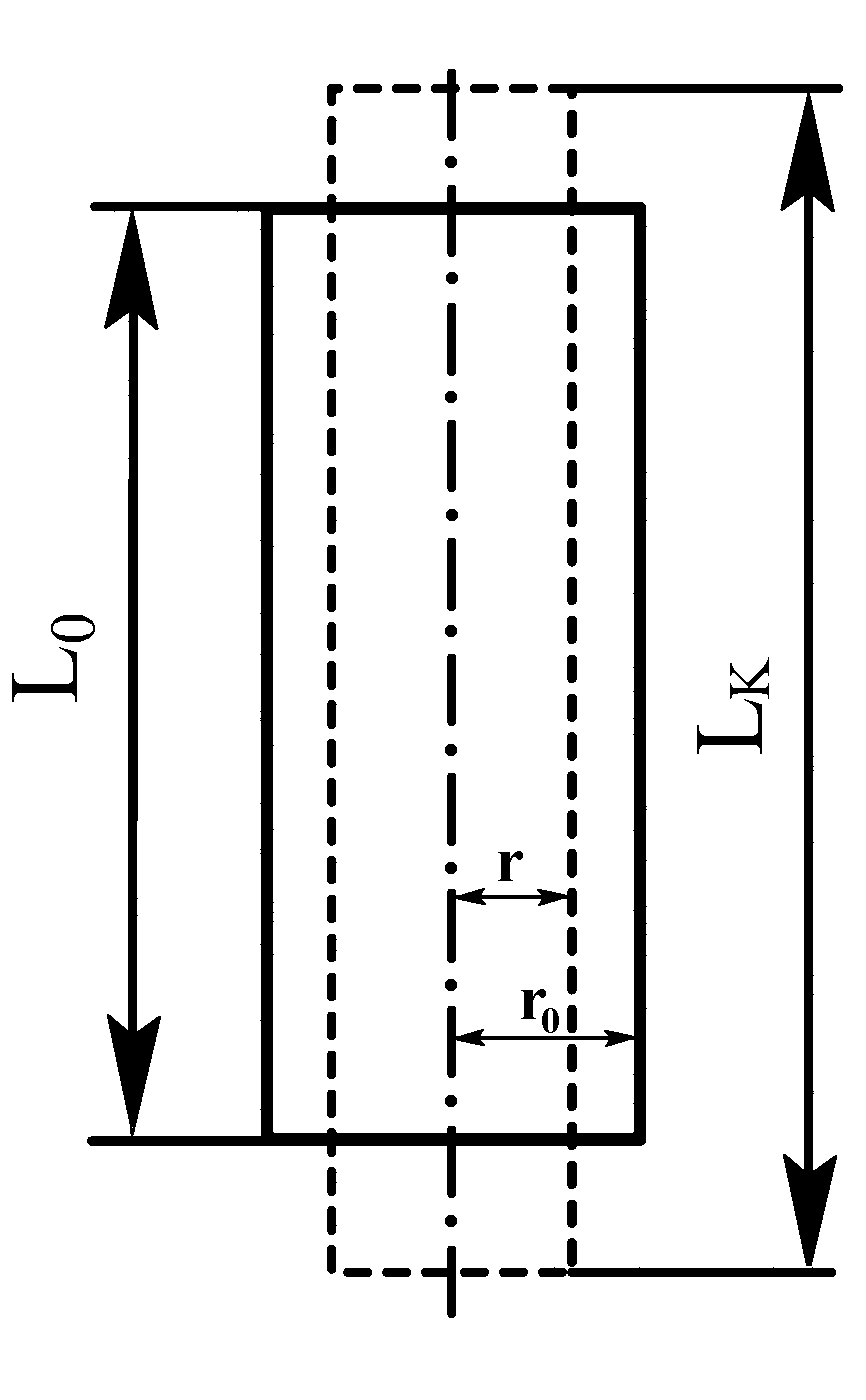
Рис. 4.4. Деформация растяжения цилиндра

Как и в случае напряжений, следует отличать условные деформации () от истинных деформаций (e)

. (4.4)

Связь между ними:

; .

Таким образом,

. (4.5)

При малых деформациях  и e совпадают. Поперечная деформация при растяжении характеризуется коэффициентом Пуассона , равным отношению изменения размеров в поперечном направлении к их изменению в продольном направлении. Обычно  = 0,25  0,35 (рис. 4.4).

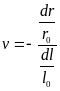. (4.6)

Диаграмма деформации для конкретного вещества отражает зависимость деформации  от приложенного напряжения  (рис. 4.5).

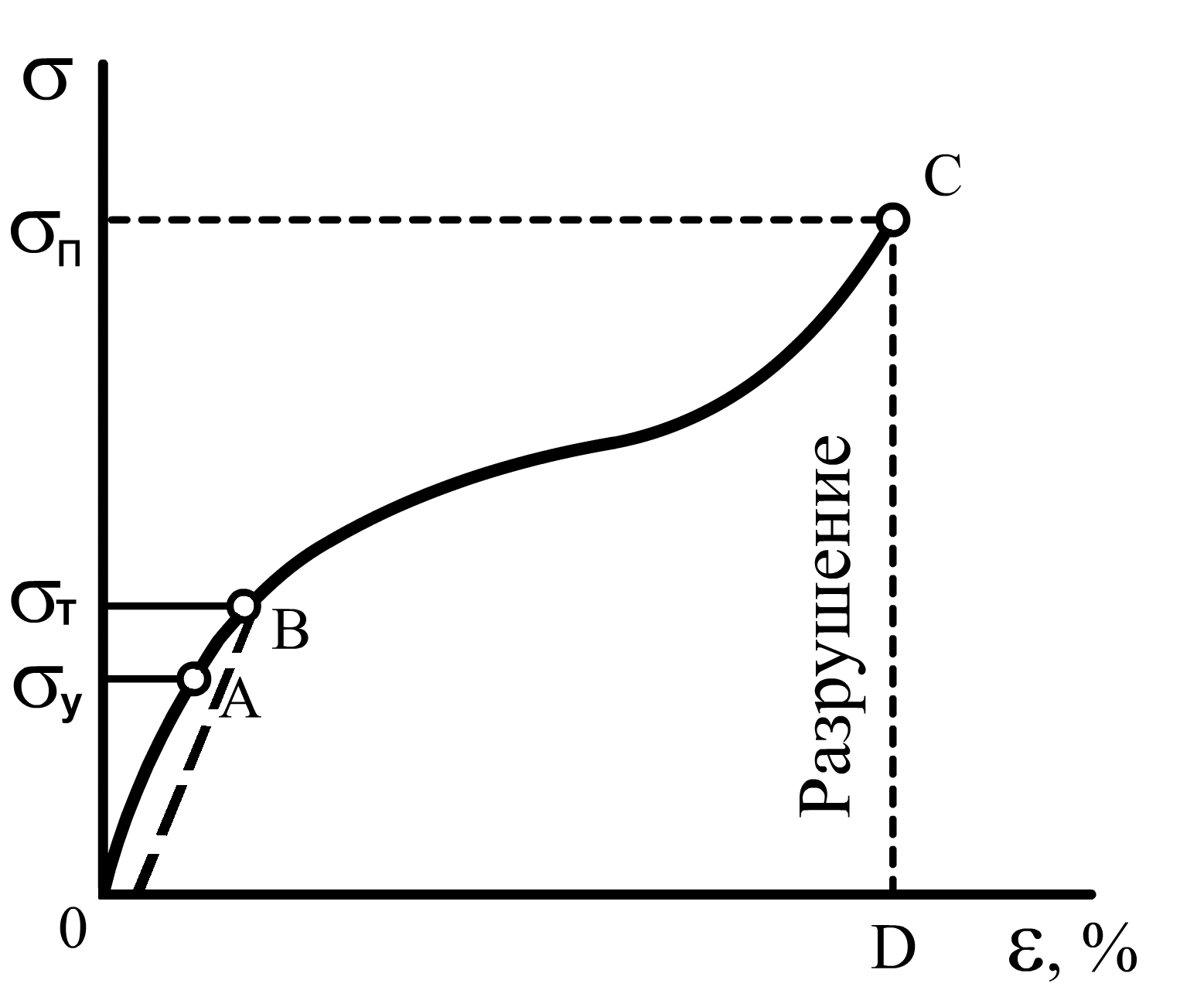
Рис. 4.5. Диаграмма деформации с площадкой текучести

Из диаграммы деформации  = f() можно узнать предел прочности твердого тела, области упругости, пластической деформации и др.

Участок ОА: упругая (обратимая) деформация ( << 1 %), область действия закона Гука; _у – предел упругости.

Участок АВ: пластическая (необратимая) деформация, после снятия напряжения размеры тела не восстанавливаются; _т – предел текучести.

Участок ВС – площадка текучести: деформация растет без значительного увеличения нагрузки; _п – предел прочности, образец разрушается.