3. Дефекты в твердых телах

Кристалл, состоящий из строго периодически расположенных атомов, имеющих фиксированные координаты, называется идеальным кристаллом. К сожалению, в природе идеальных кристаллов нет, так как все реальные кристаллы содержат различные дефекты. Например, поверхность кристалла характеризуется прерыванием периодического расположения атомов и обрывом валентных связей – это один из видов дефектов кристалла.

Любое отклонение от строго периодической структуры кристалла называется дефектом. Дефекты структуры оказывают существенное влияние на свойства твердых тел (электропроводимость, фотопроводимость, фотолюминесценция, цвет кристалла, прочность, пластичность и др.). Процессы диффузии, роста кристалла, рекристаллизации и другие можно объяснить только с помощью дефектов. Тепловые колебания атомов – тоже дефект, так как сопровождаются изменением координат атомов.

3.1. Классификация дефектов

Дефекты кристаллов можно классифицировать по геометрическим признакам.

Точечные (нульмерные) дефекты.

Размер такого дефекта соизмерим с межатомными расстояниями. Это вакансии (отсутствие атома), атомы собственной решетки в междоузлиях, атомы примесей в узлах или в междоузлиях, комплексы или кластеры примесей, примесей и вакансий и т.п., комплексы вакансий (дивакансии, тривакансии и т.д.).

Линейные (одномерные) дефекты.

Это дислокации (линейные и винтовые), микротрещины (их источник – пластическая деформация), линейные цепочки из точечных дефектов (могут возникать при облучении частицами высоких энергий) и др.

Поверхностные (двухмерные) дефекты.

Поверхность кристалла, границы зерен и двойников, дефекты упаковки, межфазные границы и др.

Объемные (трехмерные) дефекты.

Микропустоты, включения другой фазы и др. Обычно возникают при выращивании кристалла.

Наибольшее значение для полупроводников имеют точечные дефекты, которые могут возникать при нагреве или охлаждении кристаллов (тепловые дефекты), при облучении кристаллов быстрыми частицами (радиационные дефекты), при отклонении состава химического соединения от стехиометрии (стехиометрические дефекты), при пластической деформации и т.п.

Например, тепловые точечные дефекты могут быть двух типов:

1. Дефекты по Френкелю: парный дефект – вакансия плюс атом в междоузлии. Возникает за счет внутренней сублимации атомов и диффузии. Характерен для открытых решеток: Si, А³В⁵ и др. Маловероятен в плотноупакованных решетках металлов.

2. Дефекты по Шоттки: атом покидает кристалл, оставляя вакансию, которая диффундирует вглубь кристалла. Дефекты по Шоттки уменьшают плотность кристалла.

На рис. 3.1, 3.2 и 3.3 – узлы и междоузлия в ГЦК, ОЦК решетках.

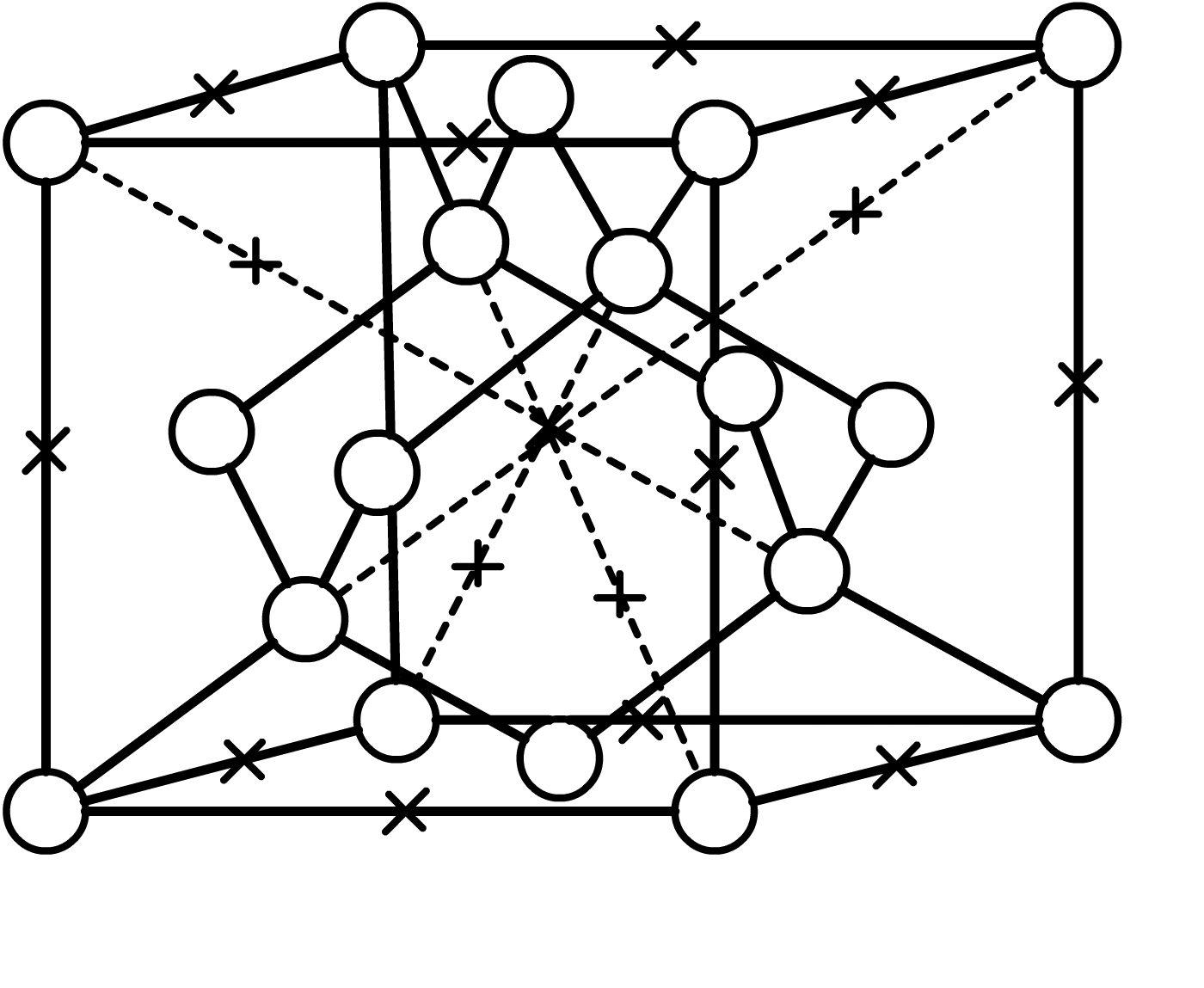
Рис. 3.1. Узлы и междоузлия в ГЦК решетке кремния

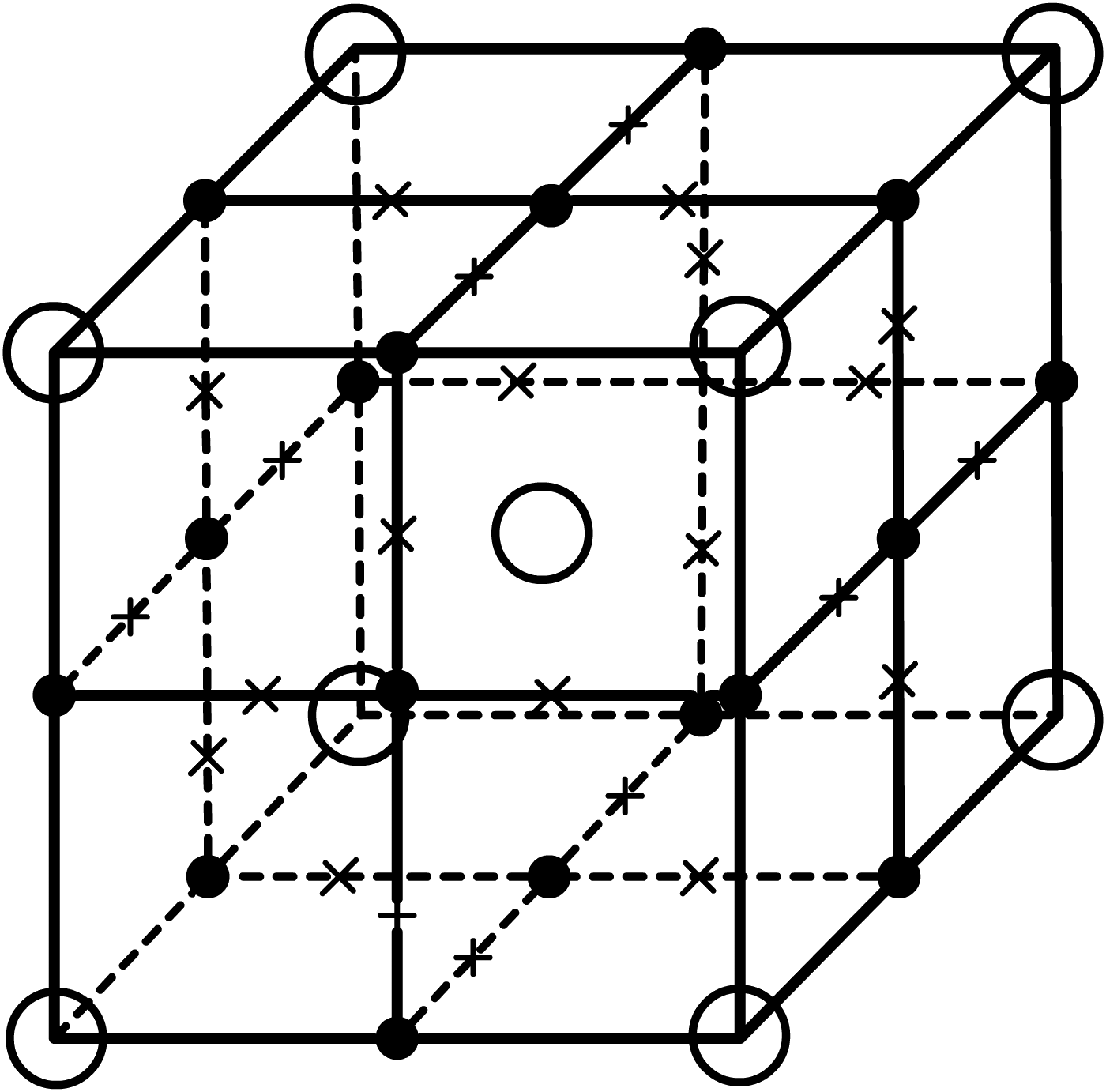
Рис. 3.2. Узлы и междоузлия в ГЦК решетке NaCl

Рис. 3.3. Узлы и междоузлия в ОЦК решетке

3.2. Термодинамически равновесная концентрация точечных дефектов

Для образования точечного дефекта необходим разрыв межатомных связей в кристалле. Например, для образования вакансии в Si требуется 2,3 эВ; в Ge  2 эВ. При высоких температурах увеличивается внутренняя энергия кристалла Е и одновременно растет энтропия. Таким образом, свободная энергия F = E – TS может быть минимальной, что соответствует состоянию термодинамического равновесия.

Оценим термодинамически равновесную концентрацию дефектов по Френкелю. Пусть для образования одного дефекта по Френкелю требуется энергия E_F, тогда при образовании n дефектов увеличение внутренней энергии составит

. (3.1)

Обозначим N и N – число атомов и междоузлий в кристалле. Найдем энтропийный множитель. Разупорядочение кристалла происходит за счет образования n вакансий и перехода n атомов в междоузлия. Увеличение энтропии:

, (3.2)

где W – термодинамическая вероятность, т.е. число способов, которыми можно получить данное состояние системы. Первое слагаемое – для узлов, а второе – для междоузлий кристалла.

Термодинамическая вероятность вычисляется как число сочетаний из N или N элементов по n.

; (3.3а)

. (3.3б)

Увеличение конфигурационной энтропии для двух независимых процессов:

. (3.4)

Выражение (3.4) можно упростить, воспользовавшись приближенной формулой Стирлинга (при больших x):

.

Таким образом,

(3.5)

Свободная энергия кристалла

. 3.6)

При термодинамическом равновесии свободная энергия F должна быть минимальна:

; (3.7а)

. (3.7б)

Таким образом, при условии термодинамического равновесия энергия образования дефекта по Френкелю равна:

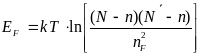. (3.8)

Так как , то равновесная концентрация дефектов по Френкелю описывается законом Аррениуса:

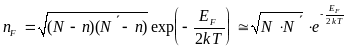. (3.9)

Аналогичный расчет для концентрации дефектов по Шоттки дает выражение:

. (3.10)

На рис. 3.4 приведена температурная зависимость концентрации равновесных дефектов, из которой можно определить энергию активации E_F дефектов по Френкелю

; (3.11а)

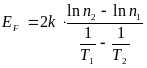. (3.11б)

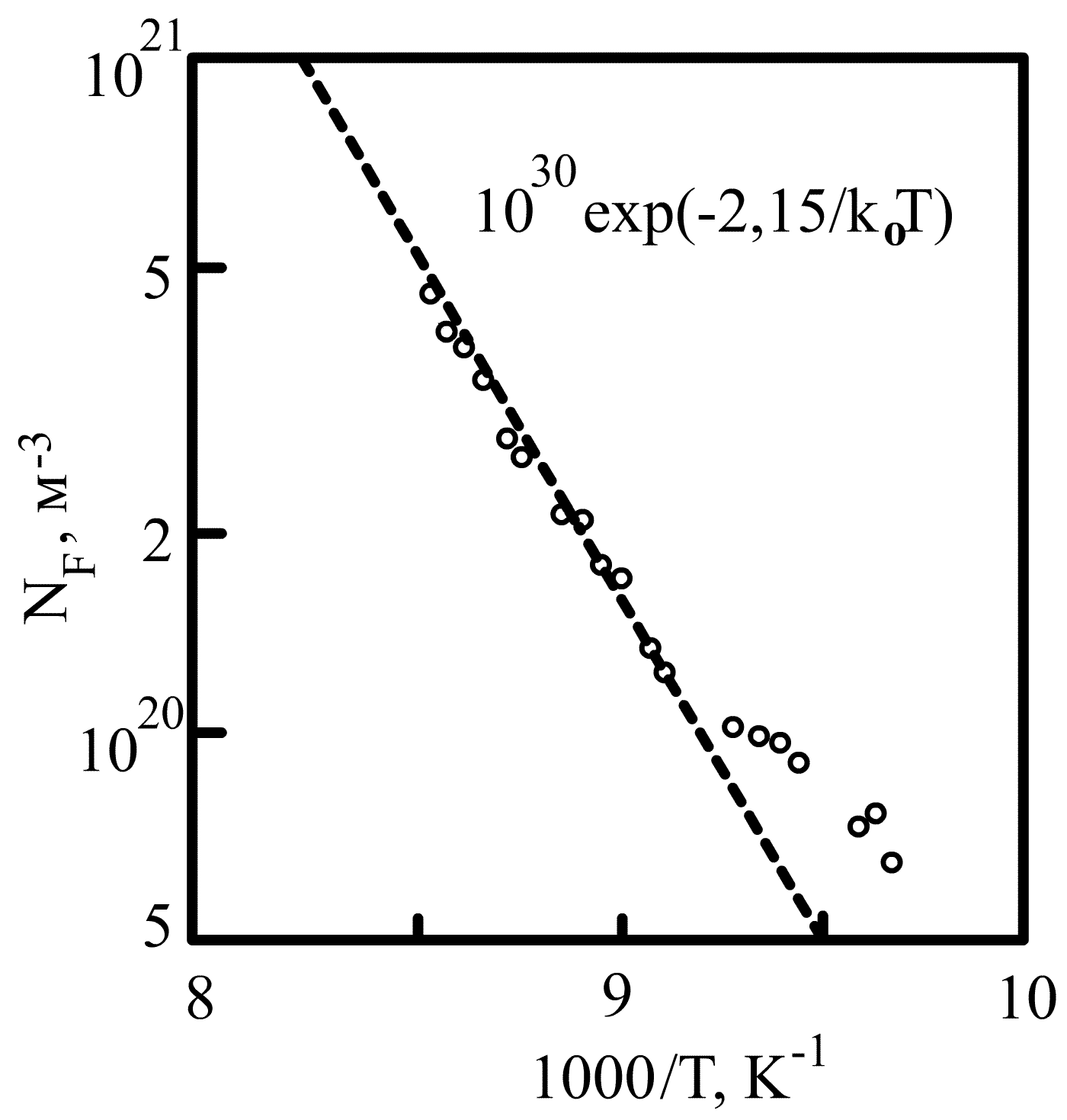
Рис. 3.4. Температурная зависимость концентрации равновесных точечных дефектов в Ge

Можно также оценить долю вакансий по отношению к концентрации атомов кристаллической решетки.