2. Структура кристаллов и способы ее определения

С точки зрения характера межатомных взаимодействий аморфные твердые тела проявляют ближний порядок в связях между ближайшими соседями, тогда как кристаллам присущ дальний порядок в расположении атомов. Дальний порядок формирует периодическую атомную решетку, определяющую многообразие форм природных и синтетических кристаллов.

2.1. Операции симметрии

Идеальный монокристалл представляет собой бесконечное повторение в трехмерном пространстве идентичных параллелепипедов (элементарных ячеек) с вершинами которых связаны атомы или молекулы.

Координаты атомов, содержащихся в узле элементарной ячейки, называются базисом кристалла. Перемещая параллелепипед элементарной ячейки с базисом на определенные дискретные расстояния во всех трех направлениях, можно заполнить все пространство кристалла. Такая операция называется трансляцией и характеризует трансляционную симметрию объекта.

Трансляционную симметрию можно описать оператором трансляции

, (2.1)

где n₁, n₂, n₃ – целые числа;

– базисные векторы.

Множество операторов трансляции определяет пространственную решетку или решетку Браве (рис. 2.1).

Понятие пространственной решетки чисто геометрическое (14 решеток). Реальная кристаллическая решетка получается, когда вокруг каждой точки решетки Браве пространство заполняется атомами, молекулами или группами атомов, формирующими базис кристалла.

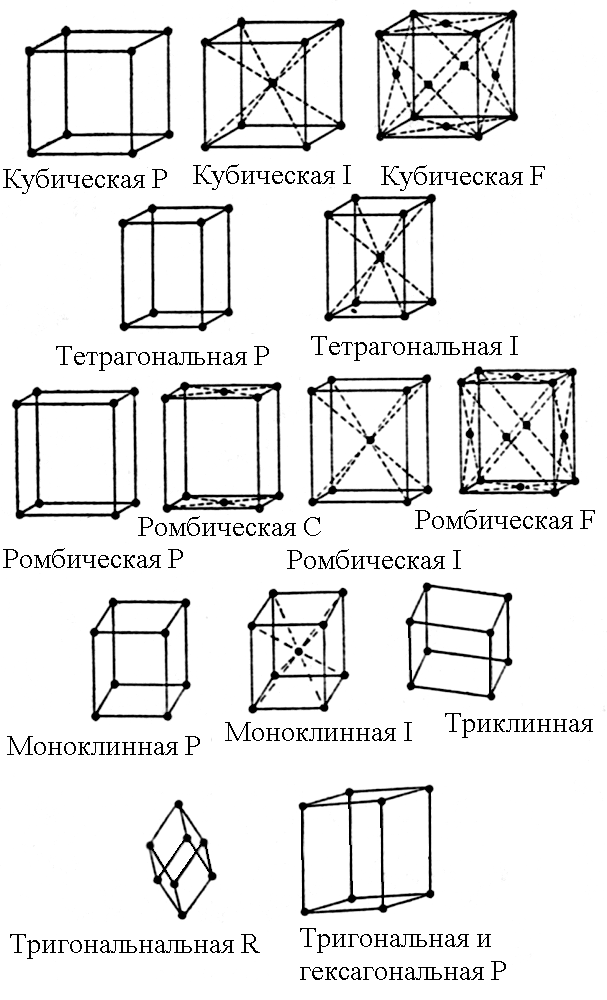
Рис. 2.1. Образование решетки Браве

Точечные группы составляют семь трехмерных кристаллических систем (сингоний)(рис. 2.2) и 14 решеток Браве(рис. 2.1).

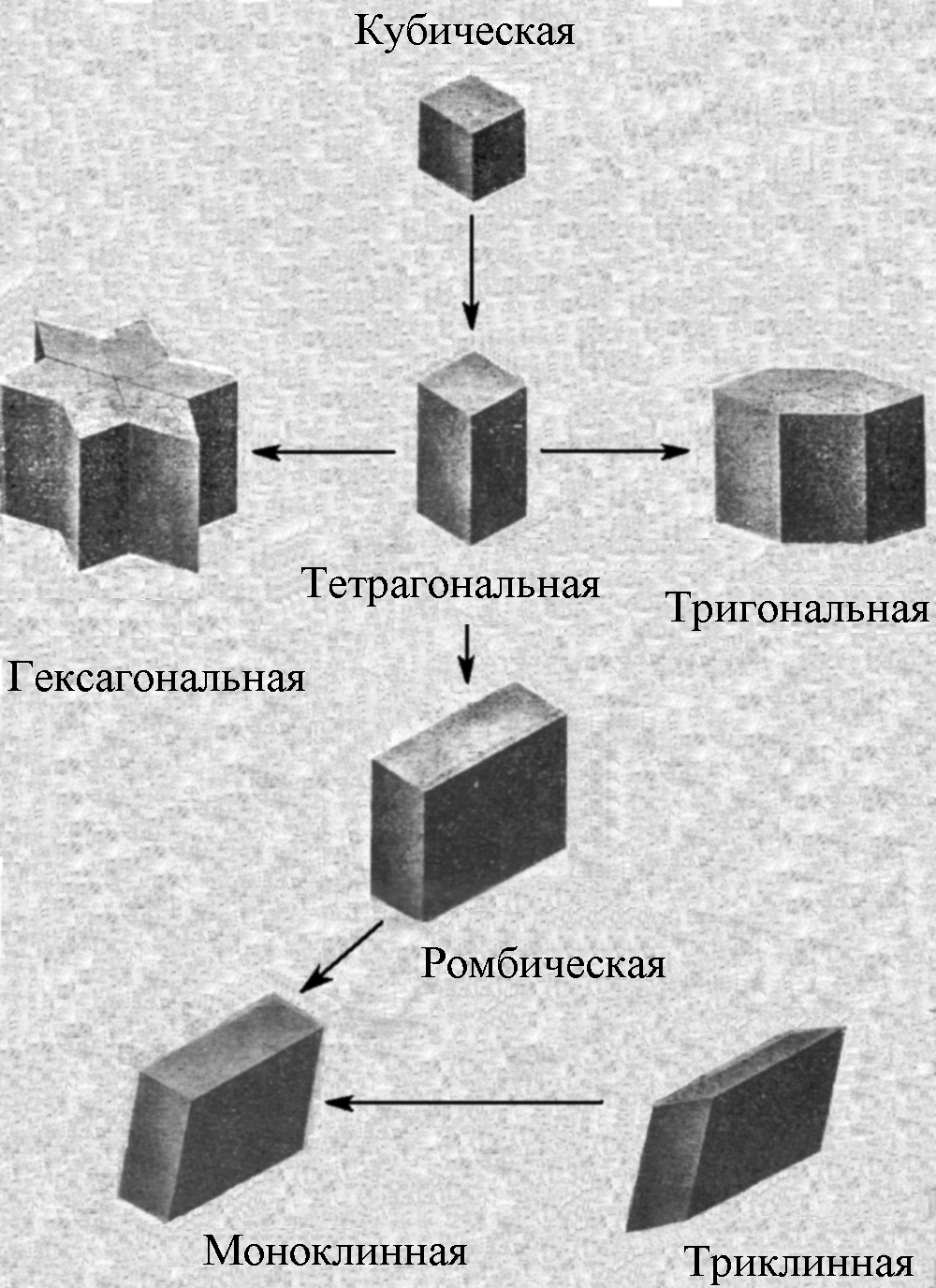
Рис. 2.2. Семь сингоний, которые можно получить деформацией кубической сингонии

Типы кристаллических решеток: Р – примитивная, R – ромбоэдрическая примитивная, C – базоцентрированная, I – объемноцентрированная, F– гранецентрированная.

Таблица 2.1

Система (сингония)	Размеры и углы элементарных ячеек	Решетки Браве
Кубическая	a = b = c  =  =  = 90	P, I, F
Гексагональная	a = b  c  =  = 90,  = 120	P
Тетрагональная	a = b  c  =  =  = 90	P, I
Тригональная (ромбоэдрическая)	a = b = c 120 >  =  =   90	R
Ромбическая	a  b  c  =  =  = 90	P, С, I, F
Триклинная	a  b  c     	P
Моноклинная	a  b  c  =  = 90  	P, I

Основные операции симметрии:

1. Отражение от плоскости (зеркальная симметрия). Обычно совпадает с одной из граней или делит ячейку пополам.

2. Ось вращения (1-го, 2-го, 3-го, 4-го или 6-го порядка), если после поворота на угол 2/n сохраняется инвариантность – совпадение точек кристалла. Оси симметрии 5-го, 7-го и 8-го порядков не сочетаются с трансляционной симметрией, так как такие обьекты не заполняют все пространство.

3. Инверсия в точке эквивалентна вращению на 180 с последующим отражением в плоскости, перпендикулярной оси вращения. Не все реальные кристаллы имеют центр инверсии, что связано с геометрическими особенностями базиса.

4. Скольжение – отражение в плоскости с одновременным переносом параллельно плоскости.

5. Винтовой поворот – вращение вокруг оси с одновременным переносом вдоль этой же оси.