Содержание

2 Интерполяция 1

2.1 Цель работы 1

2.2 Методические указания к выполнению работы 1

2.2.1 Построение интерполяционного многочлена 2

2.2.2 Сплайн-интерполяция 3

2.3 Задание на лабораторную работу 4

2.4 Пример выполнения задания 4

2.4.1 Построение интерполяционного многочлена 4

2.4.2 Программная реализация вычисления интерполяционного полинома 6

2.4.3 Построение сплайн-полинома 6

2.4.4 Программная реализация вычисления сплайн-полинома 7

2.5 Описание графического модуля 7

2.6 Индивидуальные задания 8

3 Численные методы интегрирования 11

3.1 Цель работы 11

3.2 Методические указания к выполнению работы 11

3.2.1 Интегрирование по формулам Ньютона-Котеса 11

3.2.2 Составные формулы интегрирования 12

3.2.3 Схема Ромберга 12

3.2.4 Формулы Гаусса 13

3.3 Задание на лабораторную работу 14

3.4 Пример выполнения задания 14

3.4.1 Интегрирование по схеме Ромберга 14

3.4.2 Интегрирование по формуле Гаусса-Чебышева 15

3.5 Индивидуальные задания 16

Литература 16

2 Интерполяция

2.1 Цель работы

Целью работы является изучение методов интерполяции, программная реализация этих методов.

2.2 Методические указания к выполнению работы

В процессе подготовки к лабораторной работе необходимо изучить дан­ные методические указания и конспект лекций по теме лабораторной работы.

2.2.1 Построение интерполяционного многочлена

Задача интерполяции заключается в следующем: по известным значениям функции в (n+1) точке (называемой узлом интерполяции) построить многочлен степени n ( ), служащий наилучшим приближением функции. Такой многочлен называется интерполяционным.

Интерполяционный многочлен может быть представлен в форме Лагранжа или Ньютона. Если узлы интерполяции равноотстоящие, то это упрощает построение интерполяционного многочлена.

Интерполяционный многочлен Лагранжа вычисляется согласно формуле

, (2.1)

где – узлы интерполяции, – значения функции в узлах интерполяции.

Интерполяционный многочлен Ньютона вычисляется согласно формуле

, (2.2)

где

, . (2.3)

Выражение называется разделенной разностью. Она вычис­ляется рекуррентно:

, для : . (2.4)

Интерполяционный многочлен Ньютона в равноотстоящих узлах (с шагом ) имеет вид:

, (2.5)

где , – опережающая разность k-го порядка:

. (2.6)

2.2.2 Сплайн-интерполяция

Сплайн-многочленом называется кусочно-непрерывный многочлен l-го порядка, обладающий свойством непрерывности производных до (l-1) порядка включительно. Отрезок , на котором проводится интерполяция, разбива­ется на n интервалов: , где , . Фактически сплайн-многочлен представляет собой совокупность n многочле­нов l-го порядка, коэффициенты которых подобраны так, чтобы обеспечить непрерывность производных в узлах интерполяции.

Чаще всего применяются кубические сплайны. Сплайн-многочлен для k-го интервала имеет вид:

. (2.7)

При интерполяции на равных интервалах шириной коэффи­циенты многочленов (2.7) вычисляются следующим образом:

. (2.8)

Коэффициенты находятся из системы уравнений

, . (2.9)

Эта система состоит из n-1 уравнения и содержит n+1 неизвестное. Недостающие два уравнения добавляются на основании краевых условий (а) или условий периодичности (б):

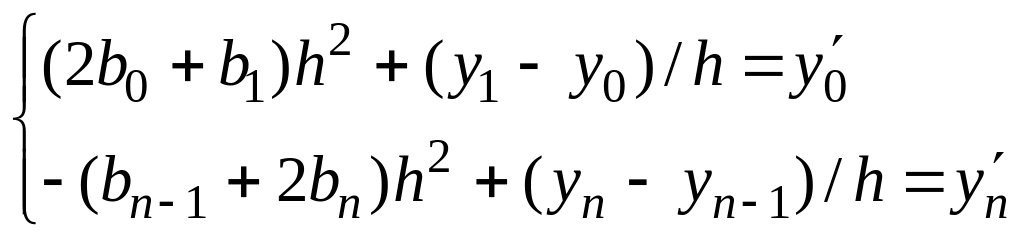, (2.10(а))

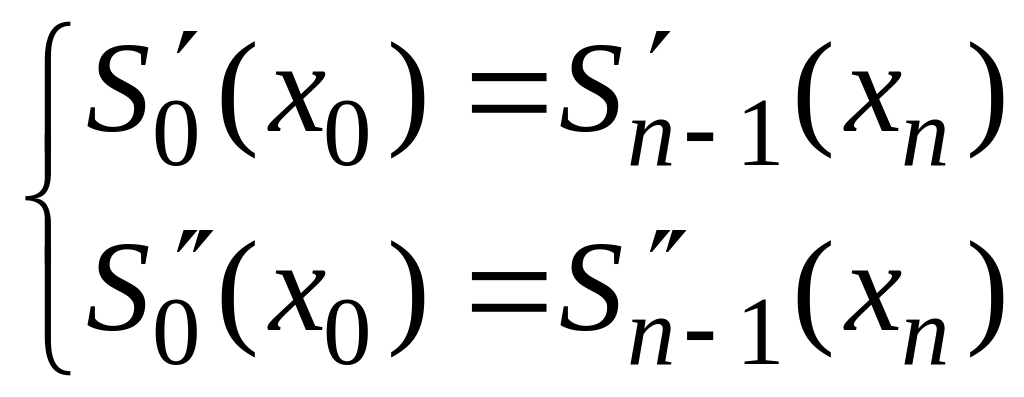
. (2.10(б))