Лабораторная работа № 2
Камеральная обработка данных стендовых испытаний ИБ на ЛГ
по дискретным алгоритмам работы БИНС с использованием пакета Matlab (Simulink)
2.1. Цель работы
Цель работы заключается в изучении дискретных алгоритмов работы БИНС при решении следующих задач:
задачи предварительной обработки данных гироскопов и акселерометров;
задачи ориентации ИБ БИИМ и объекта;
задачи преобразования сигналов акселерометров на навигационные оси и первого их интегрирования - вычисление составляющих вектора линейной скорости и вектора угловой скорости вращения географического трехгранника;
задачи вычисления координат места;
формирование управлений (демпфирующих и корректирующих сигналов) в обратной связи.
2.2. Вопросы теории
Для обеспечения устойчивой работы БИНС в условиях эксплуатации необходимо демпфирование собственных колебаний погрешностей и периодическая коррекция погрешностей выработки координат места. Для этого требуется формирование скоростных и позиционных измерений с опорой на данные внешних источников информации(GPS, лага и т.д.) [1, 2].
2.3. Основные сведения
Скоростные измерения (по GPS) для демпфирования собственных колебаний погрешностей БИНС:
(2.1)
где
приращения декартовых координат объекта
в проекциях на географические оси,
измеряемые в доплеровском канале
современной ПА GPS/ГЛОНАСС
с дискретностью
;
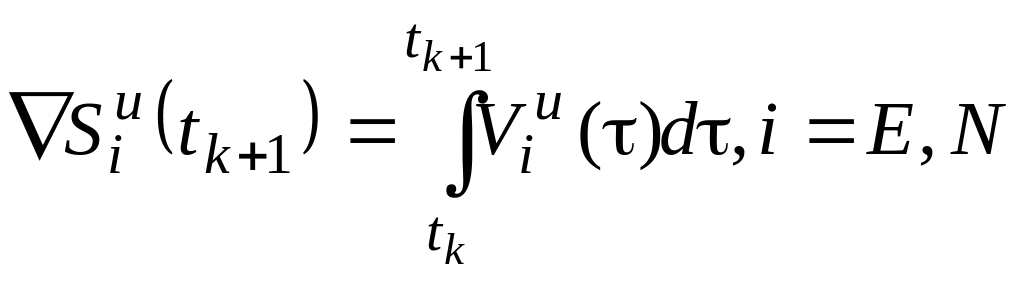
приращения декартовых координат,
вычисляемые по данным БИНС о скорости
движения объекта.
Соотношения (2.1) могут быть приведены к виду:
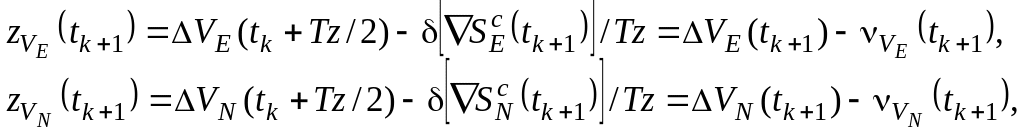(2.2)
где
погрешности доплеровского
канала ПА GPS/ГЛОНАСС;
реальные шумы скоростных измерений.
Позиционные измерения (для периодической коррекции погрешностей выработки координат места)
(2.3)
где
погрешности
дальномерного канала ПА
GPS/ГЛОНАСС;
- динамическая составляющая вертикальной
качки морского надводного объекта (с
точностью до превышения геоида), которая
может быть аппроксимирована марковским
процессом второго порядка с
м.
Курсовое измерение (привлекается в условиях стенда)
,
(2.4)
где
шумы измерений,
включающие флуктуационную составляющую.
В автономном режиме работы БИНС используются только данные относительного лага и априорная информация о высоте (глубине) корабля.
Скоростные измерения (по лагу):
(2.5)
где
и
- морские течения,
- шумы измерений, включающие неизмеряемую
лагом поперечную составляющую вектора
скорости корабля и инструментальные
погрешности лага и аппроксимированные
белыми шумами с дисперсией
на частоте 1 Гц.
Позиционное измерение (по высоте)
(2.6)
которое совпадает с третьим измерением в (2.3).
Управления (сигналы демпфирования и коррекции)
При
использовании стационарного фильтра
в интересах обеспечения минимального
времени переходных процессов в системе
управления
,
формируемые в фильтре, подаются по обеим
составляющим вектора состояния северного
и восточного каналов системы, т.е.
согласно измерениям (2.2) будем иметь:
,
,
,
,
,
,
,
,
(2.7)
где
коэффициенты демпфирования вертикали
(режим горизонтирования) и
управления в
азимутальном
канале (режим
гирокомпасирования), определяющие
«веса» поступающих измерений, выбираются
из условия обеспечения оптимальных с
точки зрения погрешностей ориентации
динамических характеристик БИНС
и могут быть выбраны из следующих
соотношений:
,
(2.8)
где
–
относительный коэффициент демпфирования,
частота колебаний
в демпфируемом контуре вертикали;
(
- соответственно суточная и шулеровская
частоты);
=
=
=1/Tz
коэффициенты
разовой коррекции по координатам места.
Линеаризованная относительно алгоритма идеальной работы модель погрешностей БИИМ в выработке параметров ориентации и навигационных параметров, включающая модели погрешностей в решении задач ориентации, преобразования сигналов акселерометров на навигационные оси и их интегрирования (вычисления составляющих векторов линейной скорости в проекциях на навигационные оси и географических координат места), может быть представлена с учетом управлений в следующем виде [1, 2]:
(2.9)
где
погрешности БИИМ в
аналитическом моделировании горизонтной
системы координат с географической
ориентацией осей (географического
сопровождающего трехгранника)
(рис. 2.1);
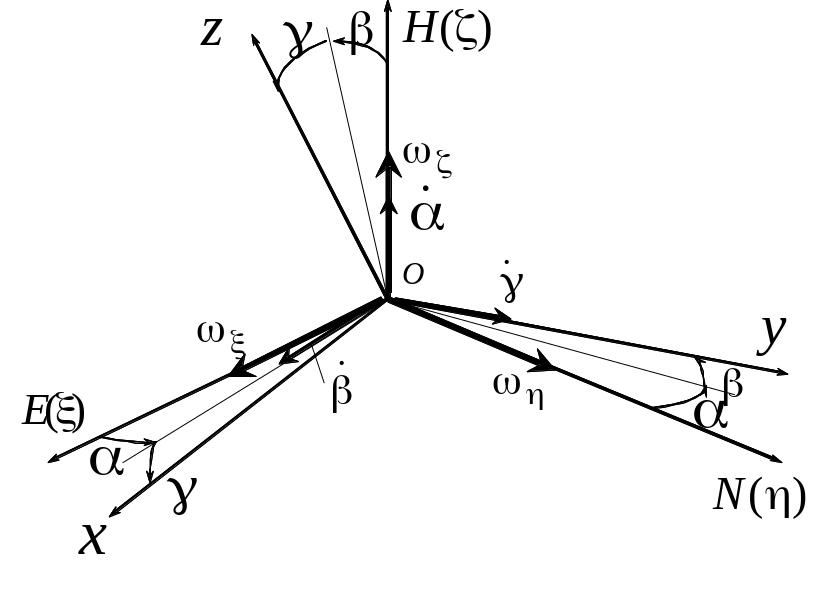
Рис.2.1. Погрешности БИИМ на ДУС в моделировании горизонтной системы координат с географической ориентацией осей
погрешности в выработке
составляющих вектора линейной скорости;
погрешности в выработке
географических широты, долготы и
высоты места;
проекции нескомпенсированных
дрейфов ДУС и так называемых "вычислительных"
дрейфов на оси горизонтной системы
координат;
проекции инструментальных погрешностей
акселерометров на оси горизонтной
системы координат;
погрешность компенсации вертикальной
составляющей вектора нормальной силы
тяжести, обусловленная погрешностями
знания координат места;
,
составляющие уклонения отвесной линии
(УОЛ) и аномалия силы тяжести;
ускорение силы
тяжести нормальной Земли;
средний радиус
Земли;
угловая скорость
суточного вращения Земли;
погрешности компенсации ”вредных”
ускорений по соответствующим осям,
выражения для которых имеют
вид:
(2.10)
составляющие угловой
скорости вращения горизонтного
трехгранника с географической ориентацией
осей, которые
определяются как
,
,
,
(2.11)
проекции кажущегося
ускорения на оси горизонтной
системы координат, которые
определяются выражениями:
(2.12)
