Дослідження цифрової фазової модуляції та демодуляції
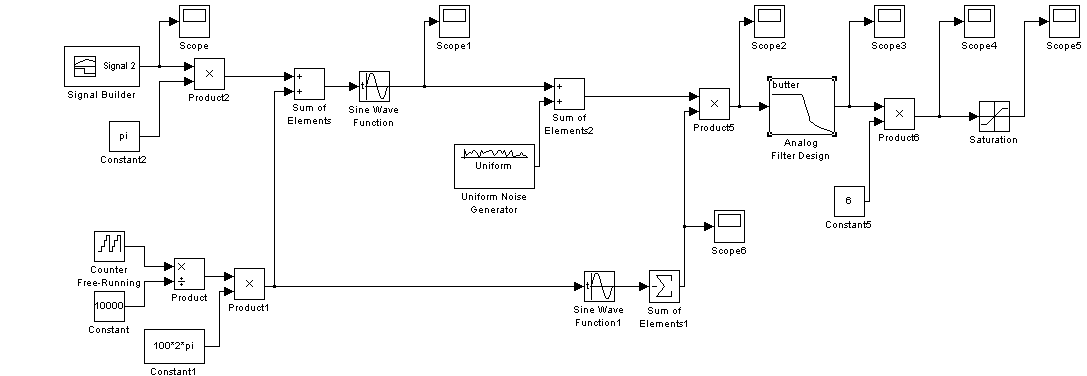
Рис. 8 Схема цифрової фазової модуляції та демодуляції.
Математичний вираз:
В елементі Signal Builder створюємо цифровий сигнал, який будемо модулювати. Він буде відповідати виразу:
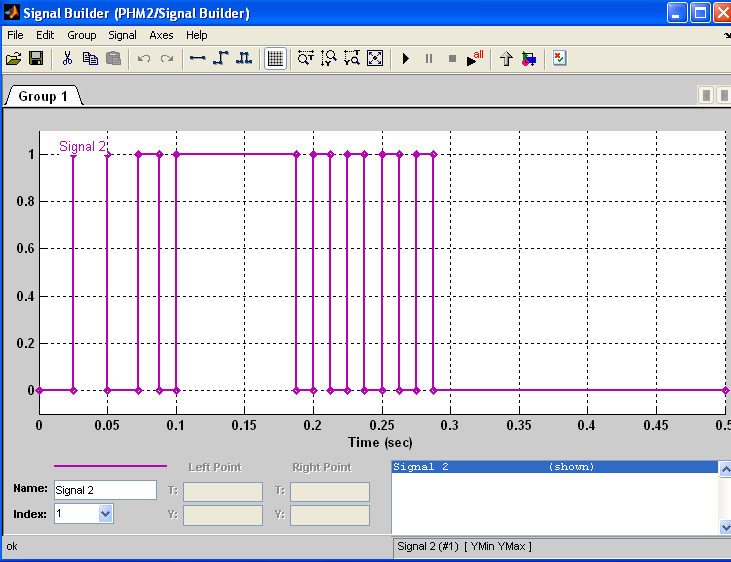
Рис. 9 Інформаційний сигнал.
Так як зміна параметра модульованого сигналу відбувається в аргументі функції sin, тому елемент Sine Wave Function перемкнемо параметр Time (t) в режим Use external signal (використати зовнішній сигнал). Це дасть нам змогу самому задавати зміну значення t функції sin(ω0t+ph). Відразу в параметрах елемента вкажемо значення частоти = 1, це дасть нам повний доступ до аргументу функції sin(ω0t+ph). Підставивши значення отримаємо функцію sin(t). Тепер t є вхідним сигналом з якого буде братися функція sin.
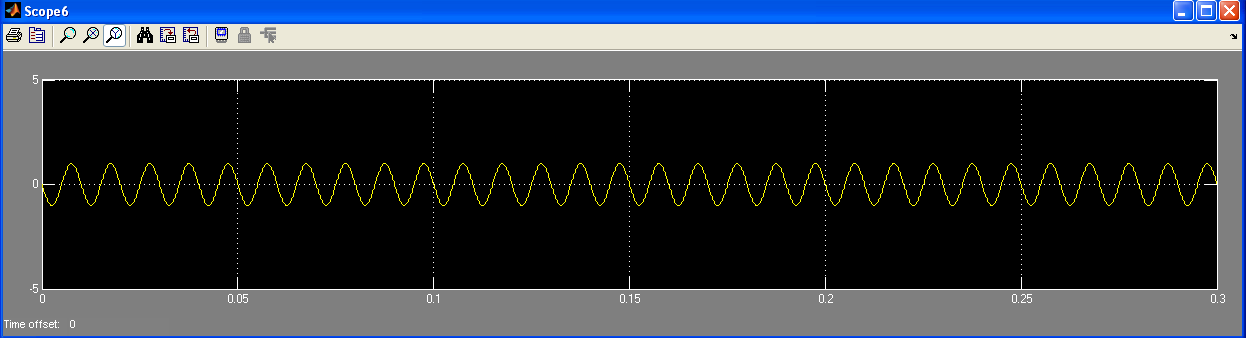
Рис. 10 Сигнал переносника
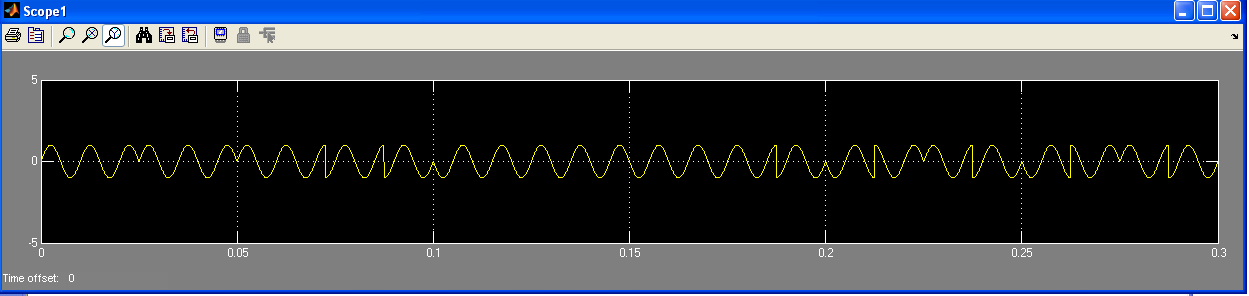
Рис. 11 Стрибки фаз модуляції
Для того, щоб зробити симуляцію зміни часу t використаємо цифровий лічильник Counter Free-Running. Так як за 0,1 с часу симуляції лічильник встигає порахувати до 1000, тому, використовуючи елемент Product, потрібно значення лічильника поділити на 10000 щоб змінна t відповідала часу симуляції. Використовуючи елемент Constant створимо число 10000. щоб поділити значення лічильника на константу в параметрі Numbers of inputs елемента Product напишемо наступне: */. В результаті цього отримаємо змінну t.
Величина ω0 – постійна. Використовуючи елемент Constant задаємо частоту сигнала-переносника.
Перемножимо ω0 і t. Якщо взяти функцію sin від цього добутку, то отримаємо модель сигнала-переносника:
Використовуючи елемент Constant створимо кут зсуву сигнала-переносника при кожному переході цифрового сигнала від 1 до 0 і від 0 до 1.
Перемножимо цифровий сигнал з кутом зсуву, використавши елемент Product.
Результат перемноження просумуємо з добутоком ω0 і t. Отриманий результат буде відповідати виразу:
Підставимо цей вираз у функцію sin. Величину Um вказуємо в параметрі Amplitude елемента Sine Wave Function. В результаті матимемо частотно-модульований цифровий сигнал.
Для імітації лінії зв’язку можемо додати завади, які виникають в лінії, з допомогою Uniform Noise Generator. В параметрах генератора задаємо верхню та нижню межу амплітуди.
З допомогою Sum of Elements сумуємо АМ-2 з завадами.
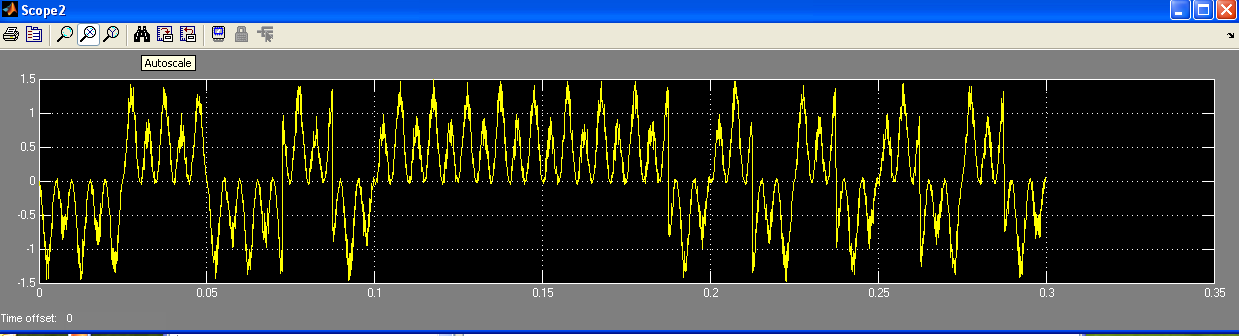
Рис.12 Сигнал із завадами
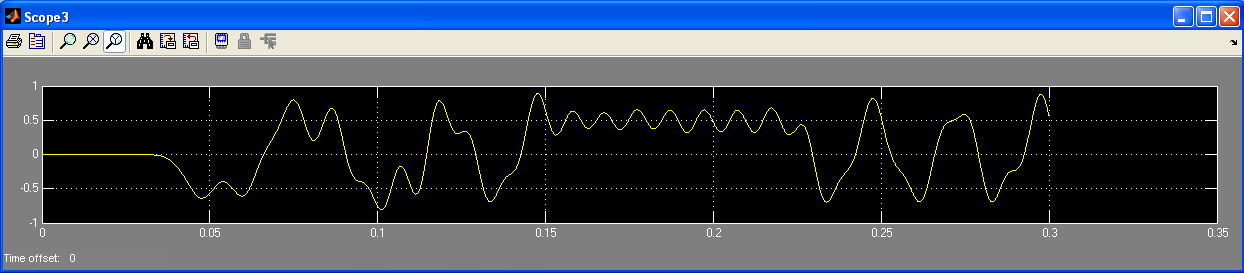
Рис.13 Сигнал після фільтра
Щоб демодулювати вхідний сигнал використаємо імпульсну демодуляцію. Для цього виконаємо наступні операції:
використовуючи елемент Product перемножимо модульований сигнал з інвертованим сигналом-переносником. Сигнал-переносник має бути таким самим, що і при модуляції;
відфільтруємо сигнал від коливань високих частот. Для цього використаємо фільтр нижніх частот Analog Filter Design. В параметрі фільтра Filter type (тип фільтрації) вибираємо Lowpass і вказуємо порядок фільтра (Filter order) та частоту зрізу;
збільшуємо амплітуду відфільтрованого сигналу в декілька разів;
використовуючи елемент Saturation обмежуємо з обох сторін амплітуду сигналу, вказавши в параметрах елемента верхню та нижню межу;
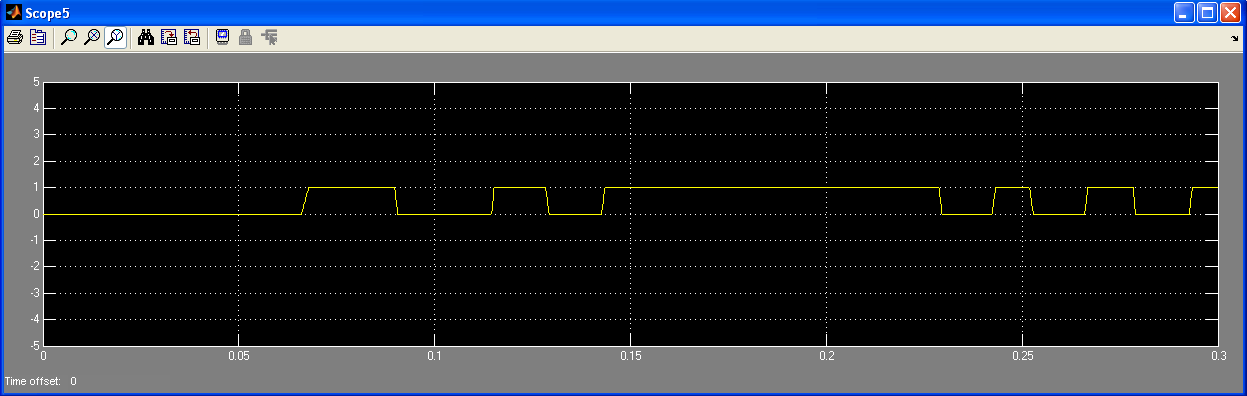
Рис.14 Сигнал який ми отримуємо на виході
Використовуючи Scope (осцилограф) можна спостерігати за формою сигналу на кожному етапі.
В результаті фільтрації отримаємо такий самий цифровий сигнал, який передавали. Але під впливом завад форма сигналу буде дещо відрізнятися, в залежності від завад.