4. Інформаційні характеристики джерела повідомлення

Кількість інформації – це логарифмічна функція ймовірності появи і вона дорівнює логарифму оберненого значення ймовірності повідомлення:

В системах, що працюють з двійковими кодами, інформація вимірюється в бітах. Ця одиниця також використовується для визначення числа двійкових символів 0 і 1, оскільки вони є рівно ймовірними і кожний із них несе 1біт інформації. Біт завжди є цілим, додатнім числом.

В залежності від визначеної розрядності визначають кількість інформації, що несуть три закодовані відліки фрагменту сигналу: І(а_і)=3 n.

4.1 Ентропія

Ентропія джерела повідомлення – це математичне очікування повідомлення. Вимірюється вона в біт/ повідомлення.

_{Поява інформації може бути рівномірною або нерівномірною. Допускаємо, що поява символів коду є рівномірною і тому за час сигналу 3t джерело повідомлення видає 3×6=18 біт.}

_{Приймемо ймовірність прийому 0,9:}

(біт/пов.)

4.2 Продуктивність джерела

Під продуктивністю джерела розуміють середню кількість інформації, утвореної джерелом за одиницю часу Т. . Якщо за час Т джерело видало n повідомлень з ентропією H(A), то продуктивність дискретного джерела повідомлень:

(біт/пов.)

(кБіт/пов.)

В результаті обчислення та застосування коректуючого коду розрядність коду збільшується і складає n = r + k: 10 = 4 + 6. Джерело повідомлення тепер буде видавати 3 × 10 = 30 (біт/с).

Ентропія:

(біт/пов.)

Продуктивність джерела:

(кБіт/пов.)

Обчислимо тривалість одного символу коду:

(мкс)

Швидкість модуляції:

В= (бод)

В= (кбод)

3. Ймовірності помилки

Інформаційна надмірність в повідомленні:

Оптимальна величина імовірності помилки:

Ре = 0,005

Ймовірність помилки із коректуючим кодом:

Рпом.n =

Рпом.n =

Ймовірність помилки без коректуючого коду:

Рпом.k =

Рпом.k =

Виграш у захисті від помилок:

а = Рпом.k/Рпом.n

а = 0,03/0,049=0,61

Коефіцієнт ефективності застосування коректую чого коду:

Кеф = 1,443 × ln(g/a)

Кеф = 1,443 × ln(1,66/0,61) = 1,44

5. Завадостійке кодування

Призначення кодера і декодера полягає в наступному. На вхід кодера надходить комбінація простого коду А_і певної довжини к, кодер перетворює її в комбінацію коректую чого коду В_і довжини n відповідно до правил кодування, причому, .На вхід декодера з каналу надходить комбінація довжини n: , де Е – комбінація помилок. Наприклад, В_і = 101000; нехай помилка відбулася в другому і третьому символах, тоді Е=011000, тоді код на вході декодера =110000.

В залежності від коректуючої здатності коду і мети його застосування декодер коректую чого коду може працювати в режимі виявлення або в режимі виправлення помилок.

В режимі виявлення помилок декодер аналізує: прийнята комбінація , дозволена чи заборонена. Якщо ця комбінація є дозволена, то декодер відповідно до правила декодування формує на своєму виході комбінацію А_і довжини к.

Якщо ж комбінація недозволена, то вона бракується декодером, і на виході декодера комбінація відсутня, а на виході сигналу помилки з’являється певний сигнал (наприклад, «1»).

В режимі виправлення помилок декодер замість забороненої комбінації декодує дозволену кодову комбінацію відповідно до правила декодування і видає комбінацію довжини к.

Для зменшення ймовірності помилки застосовують завадостійке кодування. Для цього до основного коду вводиться додатковий коректуючий код, що допомагає виявляти та виправляти помилки, що виникають в процесі передавання повідомлення в системах зв’язку. Для того, щоб коректуючий код мав коректуючи властивості, основна кодова послідовність повинна мати додаткові (збиткові) символи, призначеня для виправлення помилок. Чим більша збитковість коду, тим вища його коректуючи здатність.

Мінімальне співвідношення коректуючи та інформаційних символів . нижче якого код втрачає свої коректуючи властивості, визначається за виразом:

, де:

- кількість символів інформаційного сигналу;

кількість символів коректую чого коду

k=6, r=4: n=4+6=10

Співвідношення між кількістю символів наведено в таблиці1:

Таблиця 2 Співвідношення між кількістю символів

k	1	1	2	3	4	4	5	6	7	8	9	10	11	11
r	2	3	3	3	3	4	4	4	4	4	4	4	4	5
n	3	4	5	6	7	8	9	10	11	12	13	14	15	16

Одними із найпоширеніших систематичних кодів, що виправляють помилки, є код Хемінга та циклічний код.

Код Хемінга. Для 9-ти розрядного інформаційного коду вибираємо із таблиці кількість коректуючи символів (4) і складаємо перевірну матрицю для , в якій кожний символ повного коду закодовано бінарним кодом по вертикалі:

Н(10.4)=

0	0	0	0	0	0	0	1	1	1
0	0	0	1	1	1	1	0	0	0
0	1	1	0	0	1	1	0	0	1
1	0	1	0	1	0	1	0	1	0

На основі перевірної матриці складаємо синдром помилки, який представляє собою двійкове подання номера розряду кодової комбінації, в якій виникла помилка. Перевірні розряди синдрому розміщуються на тих місцях матриці, розряд яких має тільки один символ «1». Як видно із матриці, такими елементами є: перший, другий, четвертий та восьмий символи.

Синдром кожного для кожного рядка матриці (або символ перевірного коду) складається як сума за модулем два тільки тих символів, які місять «1»

S1= U1 + U3 + U5 + U7 + U9

S2=U2 + U3 + U6 + U7 + U10

S4=U4 = U5 + U6 + U7

S8= U8 + U9 + U10

U - умовне позначення місця символів коду у перевірній матриці.

Візьмемо інформаційний код: 101010

Символи інформаційного коду розміщуємо, залишаючи вільними місця символів 2,2,4,8, які призначені для символів коректую чого коду. Одержуємо:

-	-	1	-	0	1	0	-	1	0
U1	U2	U3	U4	U5	U6	U7	U8	U9	U10

Обчислюємо значення символів коректуючого коду із виразу синдрому помилки:

U1= U3 + U5 + U7 + U9 + U11 + U13

U1= 1 + 0 + 0 + 1 = 0

U2= U3 + U6 + U7 + U10

U2= 1 + 1 + 0 + 0 = 0

U4= U5 + U6 + U7

U4= 0 + 1 + 0 = 1

U8= U9 + U10

U8= 1 + 0 = 1

Підставивши в одержані вирази значення символів інформаційного коду, знаходимо, що коректуючий код:

U1 =0; U2 = 0; U4 = 1; U8 = 1, тобто: 0 0 1 1.

Повний закодований блок (сукупність інформаційних та коректуючих символів):

0 0 1 1 0 1 0 1 1 0

Припустимо, що шостий символ цієї кодової комбінації приймається помилковим, тобто одержують у приймачі повідомлення такого виду:

0 0 1 1 0 1 0 1 1 0

Прийнятий сигнал аналізується за синдромом помилки, тобто всі символи складаються за модулем 2.

S1= U1 + U3 + U5 + U7 + U9

S1= 1

S2= U1 + U3 + U6 + U7 + U10

S2= 0

S4= U4 + U5 + U6 + U7

S4= 0

S8= U8 + U9 + U10

S8= 1

Одержують:

S1 =1 ; S2 = 0 ; S4 = 0 ; S8 = 1 , тобто синдром помилки: 1001

Така комбінація символів відповідає координаті шостого розряду коду відповідно до перевірочної матриці. Виправлення помилки здійснюється шляхом інвертування помилкового символу.

Циклічний код. Циклічні коди широко застосовуються в системах зв’язку із-за своєї прости використання. Для опису циклічних кодів кодові комбінації представляються у вигляді поліномів.

Будь який циклічний код задається не тільки числами n і к, але і

породжуючим поліномом g(x) степені r. Циклічним кодом називається такий код, усі комбінації якого представляються поліномом степенi n-1 і менше, що діляться без залишку на породжуючий поліном.

У таблиці 3 наведені породжуючи поліноми для r=3,4,5:

r	g(x)
3	Х3 + Х2 + 1
	Х3 + Х + 1
4	Х4 + Х3 + 1
	Х4 + Х +1
5	Х5 + Х4 + Х2 + 1

Комбінація А_і =101010 відповідає поліному:

а_і(х)=х⁵ + x³ + x

Робота кодера циклічного коду зводиться до наступного. Нехай а_і(х) – поліном, що відповідає комбінації простого коду, яка надійшла на вхід кодера.

Поліном відповідає додаванню до вхідної комбінації r нулів праворуч. Виконується ділення поліному на породжуючий поліном g(x) з метою визначення залишку від ділення r(x). Цей залишок додаються до основного коду. Тоді поліном вихідного коду визначається, як: , тобто r нулів, введених у комбінацію заміщуються комбінацією, що відповідає залишку від ділення.

Розглянемо приклад формування кодової комбінації коду (10,4) з породжуючим поліномом: g(x)= Х⁵ + Х³ + X

Нехай, А_і=101010, поліном такої комбінаці є: а_і(х)=Х⁵ + Х³ + X

Тоді а_і(х)х⁴= Х⁹ + Х⁷ + Х⁵.

Виконуємо ділення поліному а_і(х)х⁴ на породжуючий поліном g(x) за правилом ділення поліномів арифметичним способом. Одержуємо залишок:

x9

+

x7

+

X5

x4

+

x3

+

1

x9

+

x8

+

x5

x5

+

x4

+

1

x8

+

x 7

x8

+

x7

+

x4

x4

X4

+

X3

+

1

Одержуємо залишок : Х³+1= r(х)

В результаті сигнал на виході декодера має вигляд:

, тобто кодова комбінація:

В_і=1010101001, в якій останні 4 символи є відтворення коректуючого коду.

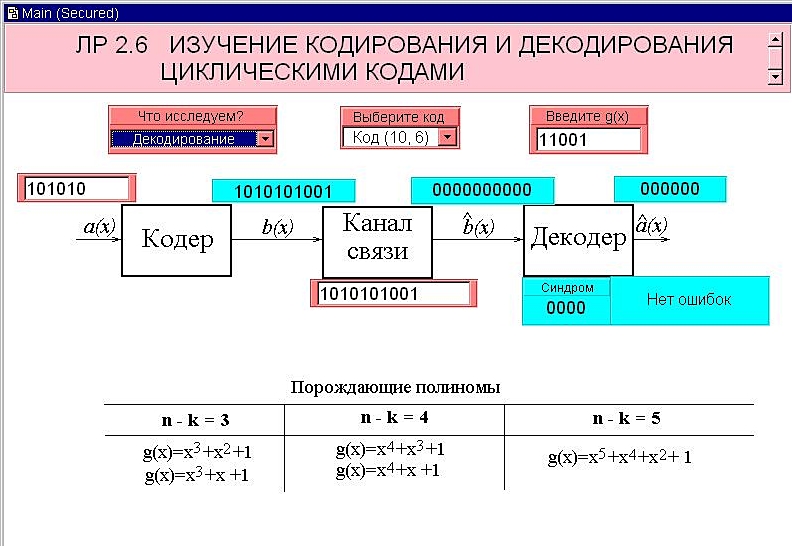
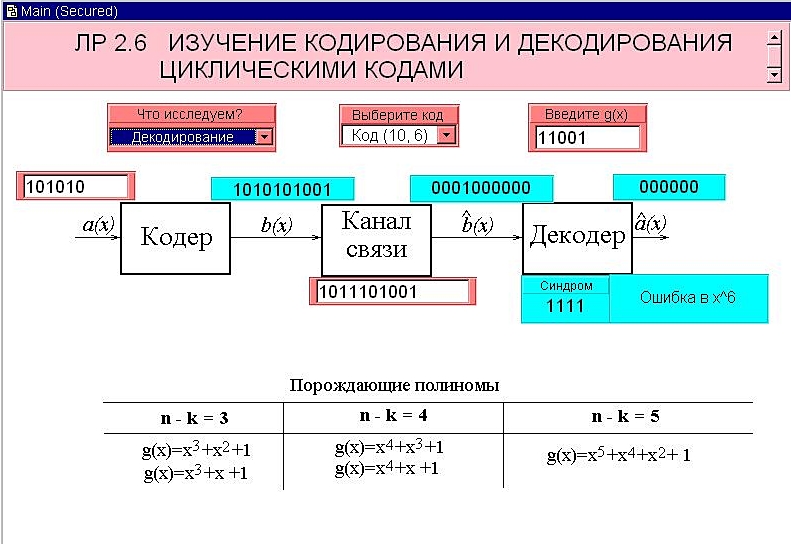
З рис. 3 Вивчення кодування та декодування циклічними кодами видно, що дійсно помилка у 6-ому розряді.