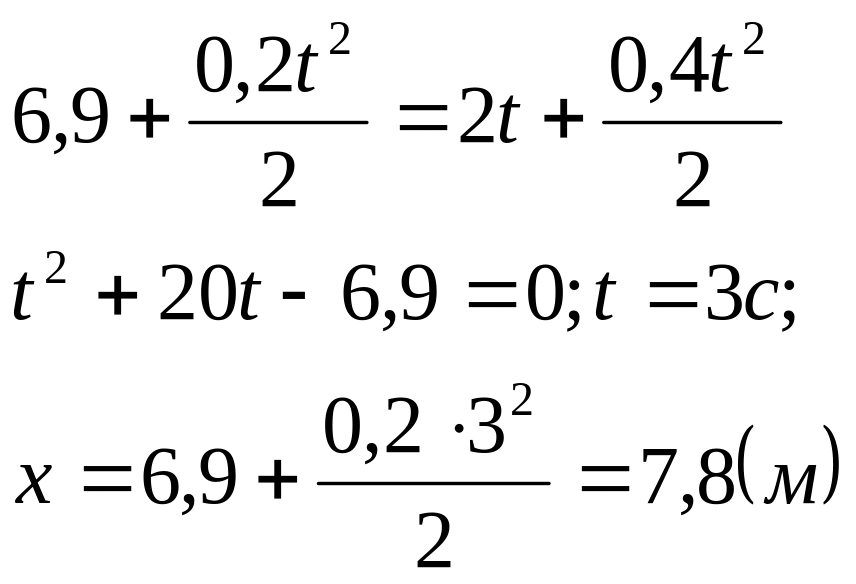Алгоритм решения задач по кинематике
При аварийном
торможении автомобиль, движущийся со
скоростью 72
,
остановился через 5
.
Найти тормозной путь.
Алгоритм |
Применение алгоритма |
1.Записать краткое условие задачи и перевести единицы измерения в единицы СИ (при решении всех задач необходимо переводить единицы измерения в одну систему).
|
|
2. Выбрать ось, вдоль которой движется тело, изобразить вектора скорости, ускорения, перемещения.
|
Вектора скорости и ускорения направлены в противоположные стороны, т. к. Скорость тела уменьшается. |
3. Записать в
векторном виде формулы, необходимые
для решения задачи (если в задаче идет
речь о перемещении и времени, то
используется формула для перемещения
с учетом времени
|
|
4. Вычеркнуть из формул величины, значения которых равны нулю.
|
|
5.
Переписать формулы в скалярном виде
с учетом знаков проекций векторов
|
|
6. Выразить из формул искомые величины и вычислить их.
|
|
,если
в задаче говорится о перемещении и не
говорится о времени, то используется
формула для перемещения без учета
времени
).
на выбранную ось.
Алгоритм решения задач, по условию которых происходит встреча тел
В момент начала
наблюдения расстояние между двумя
телами равно 6, 9
.
Первое тело движется из состояния покоя
с ускорением 0,2
.
Второе движется вслед за ним, имея
начальную скорость 2
и ускорение 0,4
.Когда
и где второе тело догонит первое?
Алгоритм |
Применение алгоритма |
1. Записать краткое условие задачи и перевести единицы измерения в одну систему. |
|
2.Выбрать ось, вдоль которой движутся тела, изобразить направления векторов скорости и ускорения движущихся тел.
|
|
3. Выбрать (произвольно) тело отсчета.
|
Тело отсчета выбираем в месте нахождения второго тела в начальный момент времени. |
4. Определить начальные координаты тел. (начальные координаты определяются для того момента времени, когда оба тела находятся в движении).
|
|
5. Записать
уравнения движения для каждого тела:
|
|
6. Записанные уравнения движения приравнять, если необходимо, дополнить их другими формулами кинематики, выразить и вычислить искомые величины.
|
|
.
При записи уравнений вместо
,
если возможно, подставляются числовые
значения. Уравнения записываются для
того момента времени, когда оба тела
находятся в движении.
Геометрический способ определения .
1. Определить
можно с помощью графика зависимости
.
Для этого надо вычислить площадь фигуры,
ограниченной графиком, осями
и
абсциссой времени, для которого
определяется скорость. .
2. Определить
можно
аналогично с помощью графика зависимости
.
3. Координата
определяется
после геометрического нахождения
по
формуле:
.
4. Пройденный путь
определяется
с помощью графика
,
при этом значения
берутся
по модулю.