КРАТКИЙ

СПРАВОЧНИК

ПО ФИЗИКЕ

Пособие для подготовки к ЕГЭ

СОДЕРЖАНИЕ

Математические основы физики ……………………………………………………4

Приставки и множители для образования десятичных дольных и кратных

единиц…………………………………………………………………………………12

Кинематика……………………………………………………………………………13

Динамика.……………………………………………………………………………..29

Статика…………………………………………………..............................................39

Импульс и закон сохранения импульса…………………………………………….41

Работа и механическая энергия……………………………………………………..45

Механические колебания……………………………………………………………49

Механические волны…………………………………………………………………54

Давление………………………………………………………………………………57

Сила Архимеда……………………………….............................................................59

Основы МКТ………………………………................................................................60

Основы термодинамики……………………………………………………………..64

Насыщенный пар и его свойства……………………………………………………72

Кристаллические и аморфные тела…………………………………………………74

Основы электростатики………………………………………………………………75

Законы постоянного тока……………………………………………………………82

Электрический ток в неметаллических средах…………………………………….86

Магнитное поле………………………………………………………………………88

Электромагнитная индукция………………………………………………………..92

Электромагнитные колебания……………………………........................................96

Электромагнитные волны…………………………………………………………..100

Геометрическая оптика……………………………………………………………..103

Волновая оптика……………………………………………………………………..110

Элементы теории относительности………………………………………………..115

Элементы квантовой физики……………………………………………………….117

Атом и атомное ядро………………………………………………………………..119

АЛГОРИТМЫ И СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Алгоритм решения задач по кинематике…………………………………………..16

Алгоритм решения задач, по условию которых происходит встреча тел………..17

Геометрический способ определения ……………………………………..19

Способ решения задач на свободное падение, если траектория не является прямолинейной………………………………………………………………………21

Способы вычисления веса тела……………………………………………………..34

Алгоритм решения задач по динамике……………………………………………..35

Алгоритм решения задач на закон сохранения импульса…………………………43

Алгоритм решения задач на закон сохранения энергии…………………………..46

Алгоритм решения задач на уравнение теплового баланса……………………….67

Способ вычисления энергии связи…………………………………………………121

Способ вычисления энергетического выхода ядерной реакции…………………122

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример решения задачи на вычисление средней скорости……………………….20

Пример решения задачи на свободное падение (прямолинейная траектория)……………………………………………………………………………21

Пример решения задачи на свободное падение, скорость направлена горизонтально………………………………………………………………………..22

Пример решения задачи на свободное падение, скорость направлена под углом к горизонту……………………………………………………………………………..24

Пример решения задачи на условие равновесия рычага…………………………..40

Пример решения задач на нахождение изменения импульса при абсолютно упругом и неупругом столкновении………………………………………………..41

Пример решения задачи на расчет КПД теплового двигателя по заданному

циклу…………………………………………………………………………………..70

Пример решения задачи на движение заряженной частицы в магнитном поле……………………………………………………………………………………91

Построение изображения в плоском зеркале………………………………………104

Примеры построения изображений в линзах………………………………………106

Пример решения задачи по геометрической оптике……………………………..109

Пример решения задачи на интерференцию света………………………………..111

Пример решения задачи на написание ядерной реакции…………………………121

Пример решения задачи на вычисление энергетического выхода ядерной реакции……………………………………………………………………………….122

Математические основы физики скалярные и векторные величины

СКАЛЯРНЫМИ величинами (скалярами) называются такие величины, которые характеризуются только числовым значением (пройденный путь l, время t, масса m, энергия Е, работа А, потенциал и др.).

Математические действия со скалярами производятся алгебраически.

ВЕКТОРНЫМИ величинами (векторами) называются такие величины, которые характеризуются числовым значением и направлением (скорость перемещение , ускорение , сила , напряженность и др.).

Способы работы с векторными величинами

1. ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ ВЕКТОРОВ.

а) Правило параллелограмма: вектора и откладываются от одной точки, результирующий вектор совпадает с диагональю параллелограмма и начинается в той же точке, от которой откладывались вектора и .

б) Правило треугольника: от конца вектора откладывается вектор начало результирующего вектора совпадает с началом вектора , а конец совпадает с концом вектора .

Для вычисления модуля результирующего вектора необходимо использовать законы геометрии (см. раздел «Соотношения в прямоугольном и произвольном треугольниках).

2. НАХОЖДЕНИЕ ПРОЕКЦИЙ ВЕКТОРОВ НА ОСИ КООРДИНАТ.

Чтобы найти проекцию вектора на ось , необходимо на эту ось опустить перпендикуляры из начала и конца вектора. Отрезок на оси между этими перпендикулярами и будет проекцией вектора на ось .

Аналогично находятся проекции на другие оси.

Проекция вектора на ось - скалярная величина, поэтому математические действия с проекциями производятся алгебраически.

Если при перемещении от начала проекции к ее концу движутся по направлению оси, то проекция вектора на эту ось положительна, в противном случае отрицательна.

Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.

Если вектор параллелен оси, то модуль проекции равен длине вектора.

Если вектор составляет некоторый угол с осью, то его проекция , .

Из рисунка видно, что (по теореме Пифагора).

Соотношения в прямоугольном и произвольном треугольниках

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

СИНУСОМ острого угла называется отношение противолежащего катета к гипотенузе.

sin =

КОСИНУСОМ острого угла называется отношение прилежащего катета к гипотенузе.

cos =

ТАНГЕНСОМ острого угла называется отношение противолежащего катета к прилежащему.

tg =

КОТАНГЕНСОМ острого угла называется отношение прилежащего катета к противолежащему.

ctg =

ТЕОРЕМА ПИФАГОРА с²= ²+ ² Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.

ПРОИЗВОЛЬНЫЙ ТРЕУГОЛЬНИК

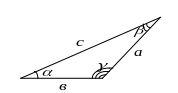
ТЕОРЕМА СИНУСОВ:

Стороны треугольника пропорциональны синусам противолежащих углов.

ТЕОРЕМА КОСИНУСОВ:

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.