МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Инженерно-экономический факультет
Кафедра эконометрики и математического моделирования (ЭиММ)
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«Математический анализ»
для направления 080100 «Экономика»
Рязань 2012
Тема 6. Определенный интеграл функции одной переменной
Лекция 1
1. Понятие определенного интеграла функции одной переменной
Пусть функция
задана на отрезке
.
Разобьем отрезок
на 
произвольных частей точками
.
Этот
набор точек
будем называть разбиением
отрезка
.
Выберем в каждом из частичных отрезков
произвольную промежуточную точку
:
,
.
Обозначим через
длину каждого частичного отрезка
.
Определение
1.
Интегральной
суммой
для функции
на отрезке
,
соответствующей данному разбиению и
данному выбору промежуточных точек
(
),
называют число
.
Определение
2.
Диаметром разбиения
называют число
.
Определение
3. Если
существует конечный предел интегральных
сумм
при
и
,
который не зависит ни от способа разбиения
отрезка
на части и не зависит от выбора точек
,
то этот предел называют определенным
интегралом от
функции
на отрезке
и обозначают
.
Определение
4. Если
определенный интеграл
существует, то функцию
называют интегрируемой
на отрезке
,
а – нижний предел, b – верхний предел, х – переменная интегрирования, – отрезок интегрирования.
2. Свойства определенного интеграла
Теорема 1.
Если функция
интегрируема на отрезке
,
то
.
Теорема 2.
Если
функция
интегрируема на отрезке
,
то
.
Теорема 3.
Если функция
интегрируема на отрезке
,
то для любых
имеет место равенство
.
Теорема 4.
Если функция
интегрируема на отрезке
и
,
то имеет место равенство
.
Теорема 5.
Если функции
и
интегрируемы на отрезке
,
то имеет место равенство
.
Теорема 6.
Если функции
и
интегрируемы на отрезке
и при всех
,
то
.
Теорема 7.
Если функция
интегрируема на отрезке
и при всех
,
то
.
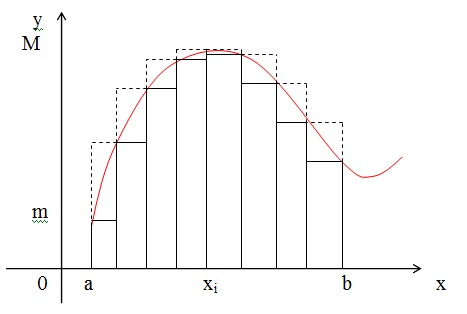
Теорема 8. Если m и M – соответственно наименьшее и наибольшее значения функции на отрезке , то:
.
Теорема 9
(теорема о среднем).
Если функция
непрерывна на отрезке
,
то на этом отрезке существует точка
такая, что
.
Лекция 2
3. Интеграл с переменным верхним пределом, его простейшие свойства. Формула Ньютона-Лейбница
Определение
1.
Пусть функция
интегрируема на отрезке
.
Функцию
(
)
назовем интегралом
с переменным верхним пределом.
Очевидно, что
,
.
Теорема 1.
Если функция
непрерывна на отрезке
,
то функция
(
)
непрерывна на отрезке
.
Теорема 2. Если функция непрерывна на отрезке , то функция ( ) на отрезке является одной из первообразных для функции , то есть
,
.
(3.1)
Следствие. Всякая непрерывная на отрезке функция имеет на этом отрезке первообразную, а значит, для этой функции существует неопределенный интеграл.
Теорема
3 (формула
Ньютона – Лейбница). Пусть
функция
непрерывна на отрезке
.
Тогда справедлива формула:
,
(3.2)
где
является первообразной для функции
на отрезке
.
Формула (3.2) называется формулой Ньютона-Лейбница вычисления определенного интеграла от функции на отрезке .
Доказательство: Пусть – первообразная для функции на отрезке . Тогда в соответствии с теоремой 9.11 функция есть первообразная для функции . Множество всех первообразных можно записать как
.
Положив в последней
формуле
и
,
получим
,
,
.
Теорема доказана.
Формула Ньютона
– Лейбница представляет собой общий
подход к нахождению определенных
интегралов. Чтобы вычислить определенный
интеграл
от функции
на отрезке
,
достаточно вычислить неопределенный
интеграл
(положить
),
затем подставить в найденную функцию
верхний предел
и нижний предел
и применить формулу (3.2). Заметим, что
если функция
имеет точки разрывов на
,
то формулой (3.2) в общем случае пользоваться
нельзя.
Пример. Вычислить определенные интегралы:
1)
;
2)
.
Решение.
1) В данном случае
функция
является непрерывной на отрезке
.
Тогда имеем первообразную
.
Применяя формулу Ньютона-Лейбница,
получим
.
2) Во втором интеграле
.
Эта функция непрерывна на области
определения
,
а отрезок
является его частью. Значит, можно
пользоваться формулой (3.2). Находим
первообразную:
.
Применяя формулу (3.2), получим
.