Лекция 3

5. Понятие предела ф1п в конечной точке, на бесконечностях. Графическая иллюстрация предела функции ф1п.

6. Понятие бесконечно-малой функции, бесконечно-большой функции, их свойства. Теорема о существовании конечного предела. Основные теоремы о пределах ф1п, свойства пределов.

5. Понятие предела ф1п в конечной точке, на бесконечностях

Пусть – функция переменной , заданная на области определения . Зададим некоторое число .

Определение 1. Точка называется предельной точкой для области определения функции , если эта функция определена на некотором малом интервале , быть может, кроме самой точки .

В математическом анализе интервал называют окрестностью точки . Согласно определению, точка может входить в область определения, а может и не входить. Главное, чтобы для этой точки можно было найти такой достаточно малый интервал, в каждой точке которого функция была определена (за исключением, быть может, самой точки ).

Отметим важный факт. Для всех основных элементарных функций, если , то точка является предельной точкой для .

Пример 1. Рассмотрим функцию 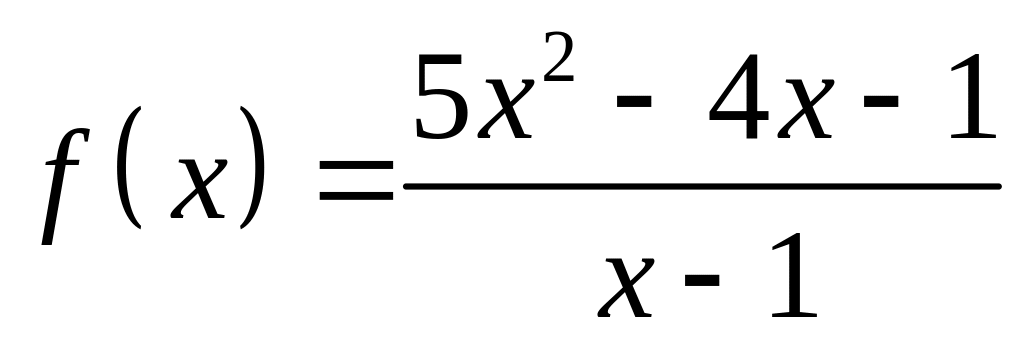. Она не определена при . Но точка является предельной точкой для области определения , так как функция определена справа и слева от точки .

Введем понятие предела функции одной переменной в конечной предельной точке . Пусть переменная приближается к точке , то есть придаем переменой значения, сколь угодно близкие к , но не равные . Это обозначаем в виде и говорим “ стремится к ”. Может оказаться при этом, что соответствующие значения функции сколь угодно мало отличаются от некоторого числа . Число называют конечным пределом функции (или просто пределом) в точке , и обозначают . При этом говорят, что функция сходится к числу при .

Определение 2. Число называется пределом функции в точке ( ), если для всех значений переменной , сколь угодно мало отличающихся от (быть может, кроме самой точки ), соответствующие значения функции сколь угодно мало отличаются от числа .

Пример 2. Пусть , – предельная точка для . Упрощая функцию, получим 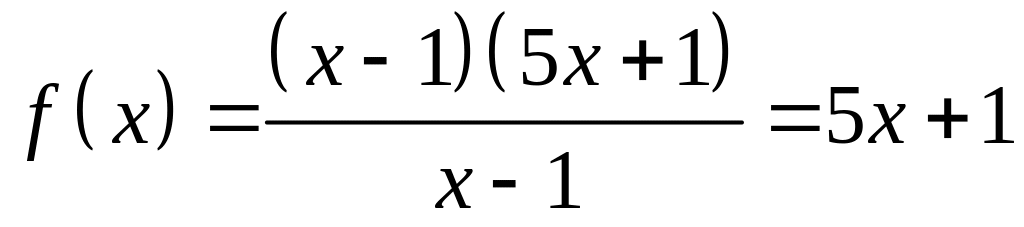(при ). Так в определении предела функции не существенно, принадлежит ли предельная точка области определения или не принадлежит, то при получаем . Значит,

.

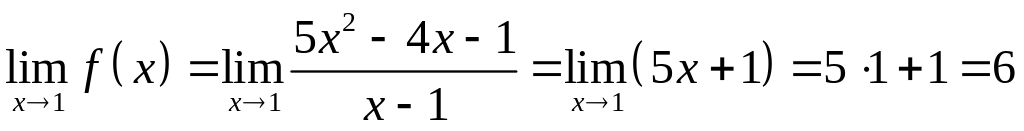Отметим важный факт, который позволяет практически вычислять пределы функций в конечных точках. Если функция является элементарной (составлена из основных элементарных функций) и точка , то предел функции в точке равен значению функции в этой точке, то есть

.

Пример 3. Вычислить: 1) 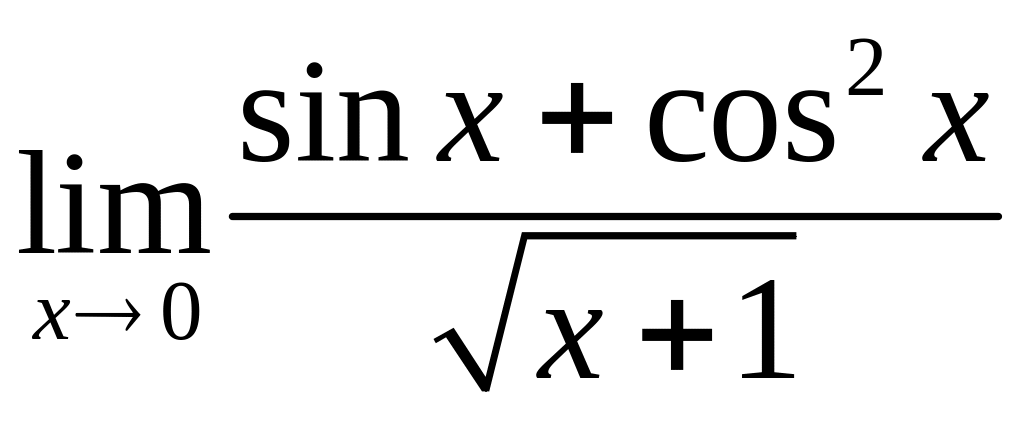; 2) .

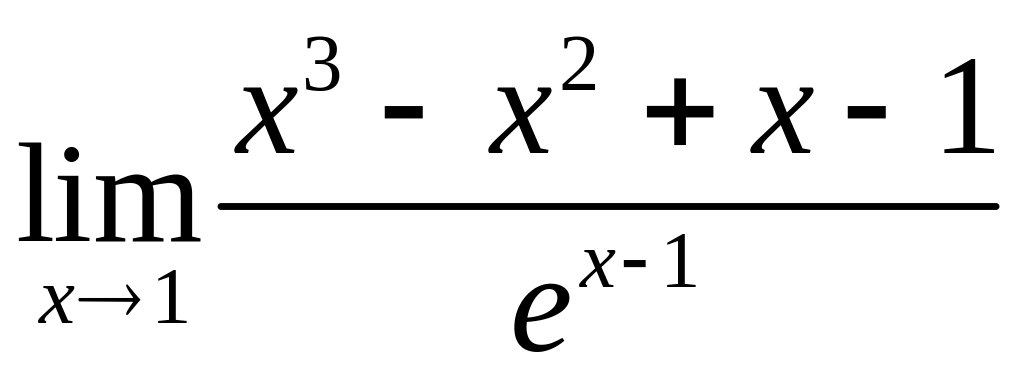Решение. 1) Имеем 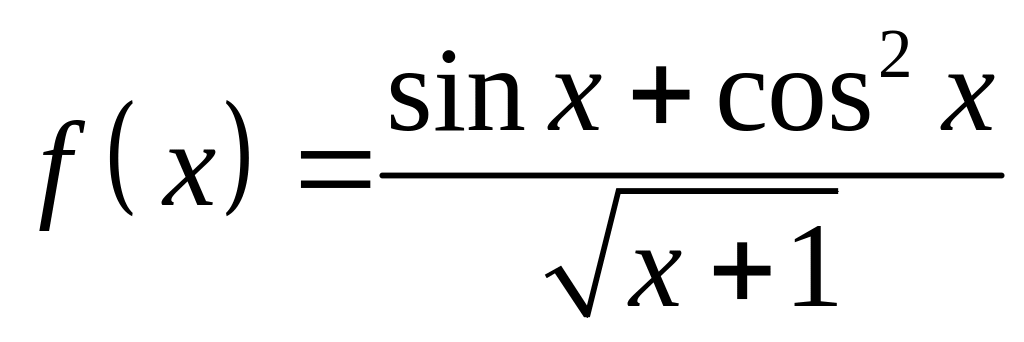, . Тогда по формуле (4.1) вычисляем (символом далее обозначаем подстановку предельной точки в функцию и называем первоначальной оценкой предела).

2) Имеем 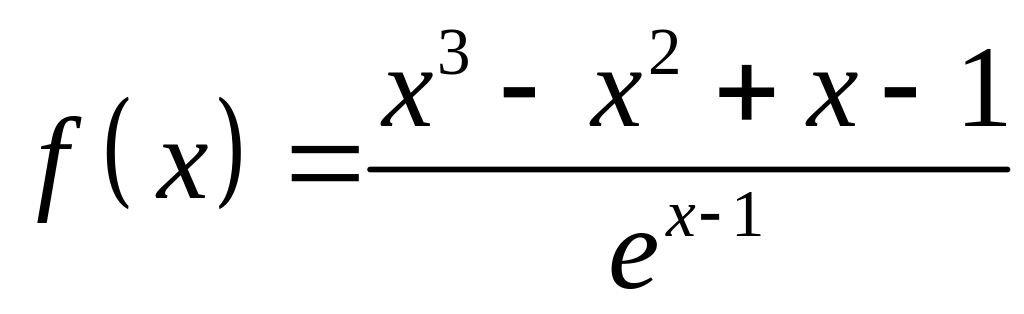, . Тогда по формуле (4.1) вычисляем .

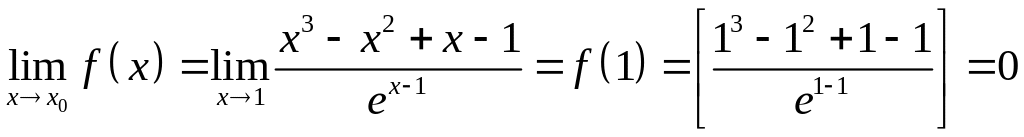Пусть функция определена на интервале . Тогда несобственную точку считают предельной точкой. Будем неограниченно увеличивать значения переменной ( ) и обозначаем . Если при этом окажется, что соответствующие значения функции сколь угодно мало отличаются от некоторого числа , то число называют пределом функции на и обозначают .

Аналогично определяют предел функции на , если функция определена на интервале и обозначают .