- •Тема 2. Функция одной переменной.
- •1. Понятие функции одной переменной (ф1п), ее способы задания. Область определения и область значений ф1п.
- •2. Основные характеристики ф1п.
- •2. Основные характеристики ф1п
- •Лекция 2
- •3. Основные элементарные функции, их графики.
- •4. Построение графиков функций: , , , , , по заданному графику функции .
- •3. Основные элементарные функции, их графики
- •1. Степенные функции
- •2. Показательные функции
- •3. Логарифмические функции
- •4. Тригонометрические функции
- •5. Обратные тригонометрические функции
- •4. Построение графиков функций: , , , , , по заданному графику функции
- •Лекция 3
- •5. Понятие предела ф1п в конечной точке, на бесконечностях. Графическая иллюстрация предела функции ф1п.
- •6. Понятие бесконечно-малой функции, бесконечно-большой функции, их свойства. Теорема о существовании конечного предела. Основные теоремы о пределах ф1п, свойства пределов.
- •5. Понятие предела ф1п в конечной точке, на бесконечностях
- •6. Понятие бесконечно-малой функции, бесконечно-большой функции, их свойства. Основные теоремы о пределах ф1п, свойства пределов
- •Лекция 4
- •7. Раскрытие неопределенности .
- •8. Раскрытие неопределенности .
- •7. Раскрытие неопределенности
- •Раскрытие неопределенности
- •Лекция 5
- •9. Первый замечательный предел. Следствия из первого замечательного предела.
- •10. Второй замечательный предел. Следствия из второго замечательного предела.
- •9. Первый замечательный предел. Следствия из первого замечательного предела
- •10. Второй замечательный предел. Следствия из второго замечательного предела.
- •Лекция 6
- •11. Односторонние пределы функции одной переменной.
- •12. Непрерывность функции, свойства непрерывных функций
- •11. Односторонние пределы функции одной переменной
- •12. Непрерывность функции, свойства непрерывных функций
- •Лекция 7 Точки разрыва функции одной переменной, классификация точек разрыва функции одной переменной
Лекция 2
3. Основные элементарные функции, их графики.
4. Построение графиков функций: , , , , , по заданному графику функции .
3. Основные элементарные функции, их графики
Определение 2.1. Основными элементарными функциями называются следующие функции (классы функций):
Степенные функции вида
 (
( );
);Показательные функции вида
 (
( );
);Логарифмические функции вида
 (
);
(
);Тригонометрические функции: , ,
 ,
,
 ;
;Обратные тригонометрические функции:
 ,
,
 ,
,
 ,
,
 .
.
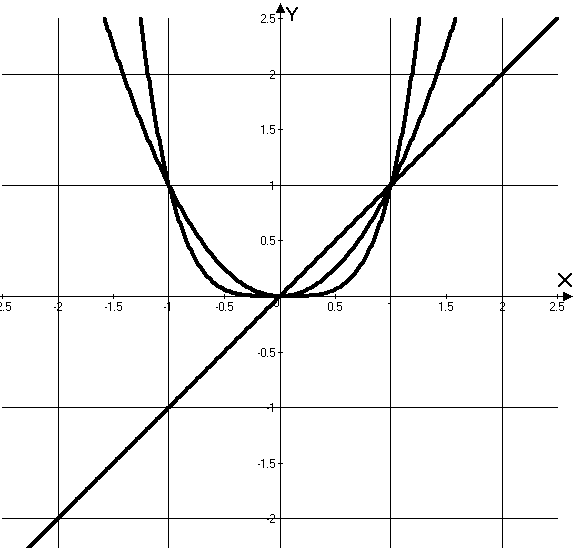
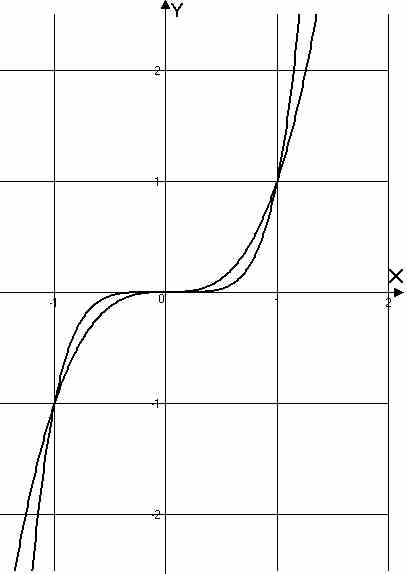
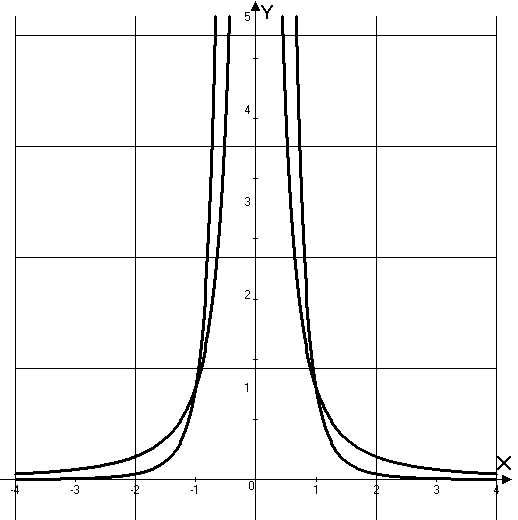
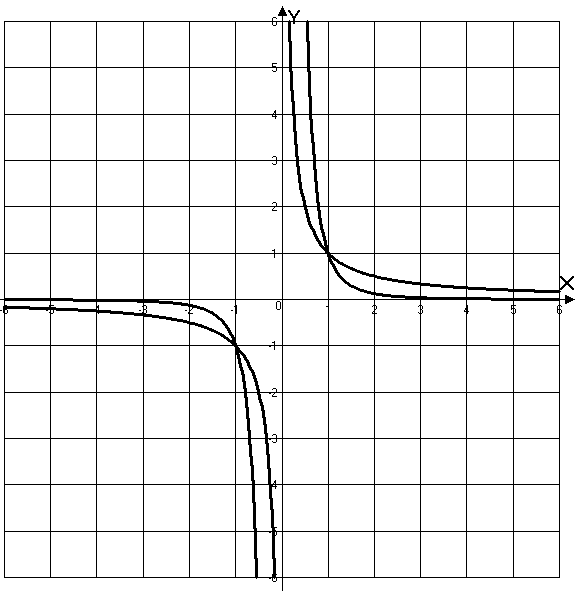
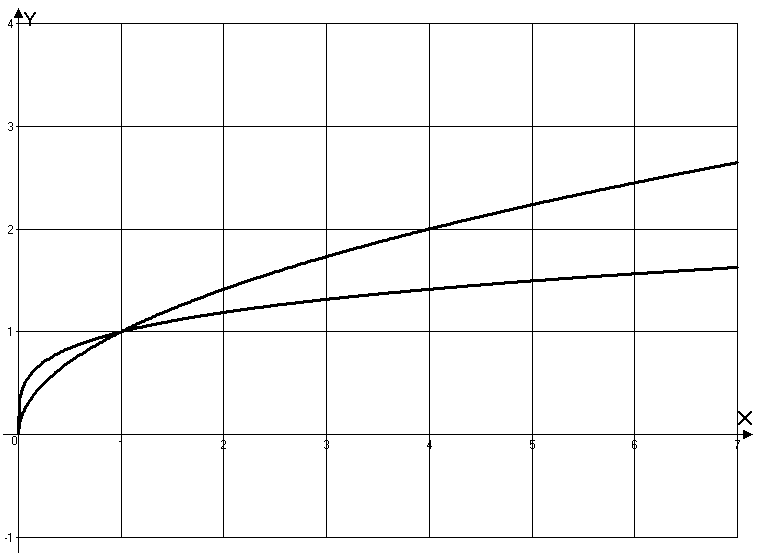
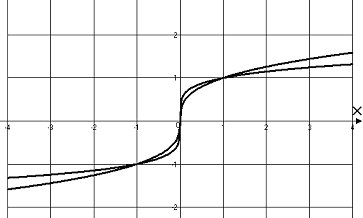
1. Степенные функции
В таблице 2.1 даны
некоторые (наиболее часто используемые)
функции,
описаны основные характеристики и
построены их графики (![]() ).
).
Таблица 2.1.
Графики элементарных степенных функций |
Степень
основные характеристики |
|
,
строго возрастающая, неограниченная, график – прямая;
четная,
строго
возрастающая на
строго
убывающая на
график – парабола;
|
|
(частные
случаи
характеристики:
нечетная, строго возрастающая; |
|
(частные
случаи
характеристики:
строго возрастающая на , строго убывающая на , неограниченная. При
неограниченном увеличении переменной
(обозначаем как
|
Соответственно
при неограниченном уменьшении
переменной ( При
стремлении переменной
к нулю (справа и слева,
|
|
|
(частные
случаи
при имеем , при имеем , прямая горизонтальная асимптота, при (справа) ,
при
(слева)
прямая вертикальная асимптота. |
|
(частные
случаи
характеристики:
строго возрастающая, неограниченная; при имеем , при имеем . |
|
(частные
случаи
характеристики:
,
при имеем , при имеем . |