МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Инженерно-экономический факультет
Кафедра эконометрики и математического моделирования (ЭиММ)
ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«Математический анализ»
для направления 080100 «Экономика»
Рязань 2012
Тема 1. Числовая последовательность, ее предел
1. Понятие числовой последовательности.
Свойства числовых последовательностей
Рассмотрим
функцию
,
где
.
Определение 1. Функцию, аргументом которой служит натуральное число n, называют числовой последовательностью.
Значения функции называются членами или элементами этой последовательности и обозначаются, как правило,
,
так что
,
,…,
.
Сокращенно
последовательность обозначается
символом
.
Геометрически последовательность
изображается на координатной прямой в
виде последовательности точек, координаты
которых равны соответствующим элементам
последовательности.
Суммой,
разностью, произведением и частным
последовательностей
и
называются соответственно последовательности
,
,
…,
,…,
,
,
…,
,…,
,
,
…,
,
…
.
Символически вышеуказанные действия записываются следующим образом:
,
,
.
Заметим,
что значения членов последовательности
не должны быть обязательно различными.
Например, если
,
,
,
то соответствующие последовательности
имеют вид
;
;
.
В первом случае имеем просто постоянную величину, во втором члены последовательности принимают два различных значения, в третьем множество значений переменной бесконечно.
Определение
2. Последовательность
назовем ограниченной
сверху (снизу),
если существует такое число
(
),
что любой элемент этой последовательности
удовлетворяет неравенству
(
).
Последовательность
называется ограниченной,
если она ограничена и снизу, и сверху,
то есть существуют такие числа
и
,
что для любого
:
.
Обозначим
.
Тогда условие ограниченности можно
записать в виде
.
Например,
последовательность
ограничена
снизу, но не ограничена сверху;
последовательность
ограничена сверху, но не ограничена
снизу;
последовательность
ограничена, так как любой элемент
этой последовательности удовлетворяет
неравенству
.
2. Предел числовой последовательности, его геометрический смысл. Свойства сходящихся числовых последовательностей
Определение
1. Число a
называется пределом
последовательности
,
если для любого положительного
,
сколь бы мало оно ни было, существует
такой номер
,
что для всех
выполняется неравенство
.
(2.1)
Тот факт, что a является пределом последовательности , записывают так:
или
. (2.2)
Если предел последовательности существует, то говорят также, что последовательность сходится.
Заметим,
что номер N
зависит от выбора
,
то есть
.
Используя логические символы, это определение можно записать следующим образом:
.
Если
изобразить числа
,
,
и значения
точками числовой оси, то получится
геометрическая интерпретация предела
последовательности (рис).
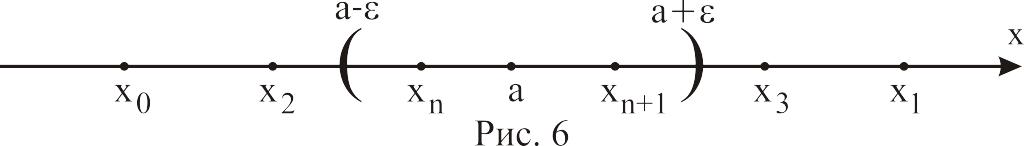
Какой
бы малый промежуток длины
с центром в точке a
ни взять, все точки
,
начиная с некоторой из них, должны
попасть внутрь этого промежутка. Особый
интерес вызывает случай, когда
,
который рассмотрим позднее.
Рассмотрим некоторые свойства сходящихся последовательностей, сформулировав их в виде теорем.
Теорема
1. Если
последовательность
имеет предел, равный a,
и
,
то и члены последовательности
,
начиная с некоторого номера.
■ Пусть
и
.
Подберем число
так, чтобы
;
для этого достаточно взять
.
Но тогда по определению предела найдется
такой номер N,
что для
выполняется
,
а, следовательно, тем более
.
■
Теорема
2. Если
и
,
то и
,
начиная с некоторого номера.
Для
доказательства следует применить
предыдущее утверждение, выбрав
.
Теорема 3. Если последовательность имеет предел, то она ограничена.
■ Так
как
,
то по определению предела последовательности
для
.
Но
,
следовательно,
;
откуда
для
.
Обозначим
.
Тогда для всех n
,
что и означает ограниченность
последовательности
.
■
Теорема 4. Последовательность не может стремиться одновременно к двум различным пределам.
■ Предположим,
что
и
,
причем
.
Выберем любое число
,
.
Так как
и
,
то существует такой номер
,
что для
(на основании теоремы 1). С другой стороны,
так как
и
,
то существует такой номер
,
что для
.
Тогда для N,
большего
и
,
одновременно и больше c
и меньше c.
Полученное противоречие доказывает
утверждение. ■