§7. Основные методы решения уравнений
1. Линейное уравнение. Линейным уравнением с одной переменной x называется уравнение вида аx + b = 0, где а, b – действительные числа. Это уравнение равносильно уравнению аx = – b.
Для линейного уравнения аx = – b возможны 3 случая:
а ≠ 0, уравнение имеет единственный корень х = –
;
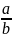а = 0, b = 0, в этом случае уравнение принимает вид 0 ∙ х = 0, х – любое число, т.е. уравнение имеет бесчисленное множество корней;
а = 0, b ≠ 0, получаем уравнение 0 ∙ х = – b, оно корней не имеет.
Пример.
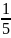х
+
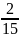= 0
По
следствию из теоремы 1 оно равносильно
уравнению
х
=
–
. Разделив обе части этого уравнения
на
,
получим х
= –
.
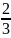2. Квадратное уравнение. Уравнение вида ах2 + bх + с = 0, где а, b, с R, а ≠ 0 называют квадратным уравнением.
Корни
уравнения находят по формуле
.
Выражение b2 – 4ас называют дискриминантом квадратного уравнения.
Если
,
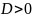то уравнение имеет 2 различных
действительных корня;
если
D
,
уравнение не имеет действительных
корней;
если D , то уравнение имеет 2 равных действительных корня.
3. Неполное квадратное уравнение. Если в квадратном уравнении ах2 + bх + с = 0 b = 0 или с = 0, то квадратное уравнение называют неполным. Для нахождения корней такого уравнения можно воспользоваться методом разложения на множители.
Пример 1. 2х2 – 5х = 0
х(2х – 5) = 0
х = 0 или 2х – 5 = 0
х
=
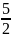
Ответ:;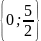
Пример 2. 2х2– 8 = 0
х2 – 4 = 0
(х – 2)(х + 2) = 0
х = 2, х = –2
Ответ: {2; –2}
4. Теорема Виета. Если приведенное квадратное уравнение х2 + pх + q = 0 имеет действительные корни, то их сумма равна –p, а произведение равно q, т.е.
х1+ х2 = –p
х1 ∙ х2 = q
х1
х2=
Пример. х2 – 9х + 14 = 0
х1+ х2 = 9
х1 ∙ х2 = 14
Такими числами являются числа 2 и 7
Ответ: {2; 7}
5. Уравнение с переменной в знаменателе.
=
0
Решение
уравнения такого вида основана на
следующем утверждении
0,
тогда только тогда, когда числитель
равен нулю, а знаменатель отличен от
нуля. Уравнение такого вида равносильна
системе:
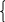=0
П
ример.
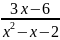=0
3х
– 6 = 0,
х2
–
х
–2
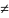0
Решая первое уравнение, получаем, что х = 2. При этом значении знаменатель х2 – х –2 обращается в нуль, следовательно, данное уравнение корней не имеет.
6.
Уравнение f(x)
= g(x)
называется рациональным,
если f(x)
и g(x)
рациональные выражения. Уравнение вида
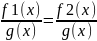равносильно системе
Пример.
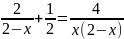
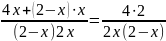
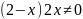
Решим
уравнение
.
x1=2;
x1=4.
Проверим, не обращают ли найденные значения переменной х знаменатель в нуль.
(2 – 2) ∙2 ∙ 2 0 – ложь, (2 – 4) ∙2 ∙ 4 0 – истина.
Ответ: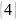
7.
Решение уравнения
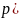)=0.
Методом разложения левой части на
множители.
Пусть надо решить уравнение ) =0, где ) многочлен степени n. Предположим, что нам удалось разложить многочлен на множители: р(х) = р1(х) ∙ р2(х) ∙ … ∙ рп(х).
Тогда уравнение примет вид р1(х) ∙ р2(х) ∙ … ∙ рп(х) = 0.
Произведение равно нулю, когда хотя бы один из множителей равен нулю, следовательно данное уравнение выглядит равносильно совокупности р1(х) = 0 р2(х) = 0 … рп(х) = 0.
Пример.
x3 + 2x2 + 3x + 6 = 0
(x3+3x) + (2x2 + 6) = 0
х(x2 + 3) + 2(x2 + 3) = 0
(х+2) ∙ (x2 + 3) = 0
х
+ 2 = 0,
x2 + 3 = 0. Из первого уравнения находим, что х = –2, второе уравнение корней не имеет.
Ответ: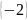
8. Решение уравнений методом введения новой переменной.
Суть этого метода покажем на примере.
Пример. (х2 – 3х)2 + 3(х2 –3х) –28 = 0
Положим, что х2 – 3х = у, тогда получим уравнение у2 + 3у – 28 = 0, откуда у1= –7, у2 = 4.
Задача сводится к решению двух уравнений х2 – 3х = – 7 и х2 – 3х = 4.
У первого уравнения дискриминант меньше нуля, поэтому оно корней не имеет; корни второго уравнения 4 и – 1.
Ответ: {4; – 1}.
9. Биквадратное уравнение.
Биквадратным
называется уравнение вида ах4
+
bх2
+
с
=
0, где а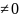
.
Решается такое уравнение методом введения новой переменой х2 = у.
Пример.
х4 + 4х2 – 21 = 0
Введем новую переменную х2 = у. Получим уравнение у2 + 4у – 21 = 0
у1 = –7, у2 = 3.
Вернемся к переменной х.
Получим
х2
=
–7 (уравнение корней не имеет), х2
=
3 (х1
=
,
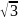х2
=
,
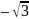Ответ:
{
}
10. Графическое решение уравнений.
Строит график функции у = f(x) и находят точки пересечения графика с осью абсцисс. Абсциссы этих точек и являются корнями уравнения.