§ 5. Классификация выражений с переменной

1) Выражение, составленное из переменных и чисел с помощью только операций сложения, вычитания, умножения, возведения в степень, называется целым выражением или многочленом.

Пример. (3х² + 5) ∙ (2х – 3у)

2) Рациональным называется выражение, построенное из переменных и чисел с помощью операций сложения, вычитания, умножения, деления, возведения в степень. Рациональное выражение можно представить в виде отношения двух целых выражений, т.е. многочленов. Заметим, что целые выражения являются частным случаем рациональных.

Пример. .

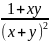3) Иррациональным называется выражение, построенное из переменных и чисел с помощью операций сложения, вычитания, умножения, деления, возведения в степень, а также операциии извлечения корня п-ой степени.

Пример. .

§ 6. Уравнения с одной переменной. Равносильные уравнения

Определение. Пусть f(x) и g(x) – два выражения с переменной х и областью определения Х. Тогда предикат f(x) = g(x) называется уравнением с одной переменной.

Определение. Значение переменной х из множества Х при котором уравнение обращается в истинное числовое равенство, называется корнем уравнения или его решением.

Решить уравнение – это значит найти множество его корней.

Пример. 1) 7х + 5 = 3х + 13, х R. Это уравнение обращается в истинное равенство при х = 2, следовательно, множество его решений есть {2}.

2) (х – 3)(х + 3) = 0 – множество решений есть {–3; 3}.

Т.к. уравнение есть предикат, то с каждым уравнением связаны два множества:

1. множество Х допустимых значений переменной (множество определения предиката),

2. множество Т корней уравнений (множество истинности предиката).

Заметим, что Т  Х.

Определение. Пусть на множестве Х заданы два уравнения f₁(x) = g₁(x) и f₂(x) = g₂(x) и известно, что Т₁ – множество решений первого уравнения (Т₁  Х), Т₂ – множество решений второго уравнения (Т₂  Х). Если Т₁ = Т₂, то эти уравнения называются равносильными на множестве Х.

Другими словами: два уравнения называются равносильными на множестве Х, если множества решений этих уравнений, принадлежащих множеству Х, совпадают.

Пример. 1) 3х + 5 = 4х + 3 и 2х + 3 = 7 равносильны на множестве N, т.к. Т₁ = {2}, Т₂ = {2}, Т₁ = Т₂.

2) (х – 2)² = 3(х – 2) и (х – 2) = 3 не являются равносильными, т.к. Т₁ = {2; 5}, Т₂ = {5}, Т₁  Т₂.

Определение. Если множество решений уравнения f₁(x) = g₁(x) (1) является подмножеством множества решений уравнения f₂(x) = g₂(x) (2), то уравнение (2) называют следствием уравнения (1).

Другими словами: уравнение (2) есть следствие уравнения (1), если каждый корень уравнения (1) является корнем уравнения (2).

Пример. (х + 2)² = 25 является следствием уравнения х + 2 = 5, т.к. уравнение х + 2 = 5 имеет только один корень 3, подставляя который в уравнение (х + 2)² = 25, получаем истинное равенство (3 + 2)² = 25, показывающее, что 3 удовлетворяет уравнению (х + 2)² = 25.

Два уравнения равносильны в том и только том случае, когда каждое из них является следствием другого.

Теоремы о равносильности уравнений

Теорема 1. Пусть уравнение f(x) = g(x) задано на множестве Х и h(х) – выражение, определенное на том же множестве Х. Тогда уравнения f(x) = g(x) (1) и f(x) + h(х) = g(x) + h(х) (2) равносильны.

Другими словами: если к обеим частям уравнения с областью определения Х прибавить одно и то же выражение с переменной, определенное на том же множестве Х, получим новое уравнение, равносильное данному.

Доказательство. Обозначим через Т₁ множество решения уравнения (1), Т₂ – множество решения уравнения (2). Уравнения (1) и (2) равносильны, если Т₁ = Т₂, т.е. Т₁  Т₂  Т₂  Т₁.

1. Докажем, что Т₁  Т₂. Пусть а – корень уравнения (1), т.е. а  Т₁ и при подстановке в уравнение (1) обращает его в истинное числовое равенство f(а) = g(а), а выражение h(х) обращает в числовое выражение h(а), имеющее смысл на множестве Х. Прибавим к обеим частям истинного равенства f(а) = g(а) числовое выражение h(а). Согласно свойствам истинных числовых равенств получим истинное числовое равенство f(а) + h(а) = g(а) + h(а), которое говорит о том, что число а есть корень уравнения (2), т.е. а  Т₁, следовательно, Т₁  Т_2.

2. Докажем, что Т₂  Т₁. Пусть а – корень уравнения (2), тогда f(а) + h(а) = g(а) + h(а) –истинное числовое равенство. Прибавив к обеим частям этого равенства числовое выражение – h(а), снова получим истинное числовое равенство f(а) = g(а). Это значит, что а – корень уравнения (1), т.е. а  Т₁, следовательно, Т₂  Т_1.

Т.к. Т₁  Т₂  Т₂  Т₁  Т₁ = Т₂, т.е. уравнения (1) и (2) равносильны на множестве Х.

При решении уравнений чаще используются следствия из теоремы.

Следствие 1. Если к обеим частям уравнения прибавить одно и то же число, то получим уравнение, равносильное данному.

Следствие 2. Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части уравнения в другую, поменяв знак слагаемого на противоположный, то получим уравнение, равносильное данному.

Теорема 2. Пусть уравнение f(x) = g(x) задано на множестве Х и h(х) – выражение, определенное на том же множестве Х и не обращающееся в нуль ни при каких значениях х из множества Х. Тогда уравнения f(x) = g(x) (1) и f(x) ∙ h(х) = g(x) ∙ h(х) (2) равносильны на множестве Х.

Другими словами: если обе части уравнения с областью определения Х умножить на одно и то же выражение с переменной, которое определено на том же множестве и не обращающееся на нем в нуль, то получим новое уравнение, равносильное данному.

Доказательство. 1) Докажем, что Т₁  Т₂. Пусть а – корень уравнения (1), тогда f(а) = g(а) – истинное числовое равенство. Умножим обе его части на числовое выражение h(а). Получим истинное числовое равенство f(а) ∙ h(а) = g(а) ∙ h(а), которое говорит о том, что число а есть корень уравнения (2), т.е. а  Т₁, следовательно, Т₁  Т_2.

2) Докажем, что Т₂  Т₁. Пусть а – корень уравнения (2), тогда f(а) ∙ h(а) = g(а) ∙ h(а) – истинное числовое равенство. Умножим обе части этого равенства на числовое выражение 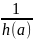(h(а) существует и нигде не обращается в нуль, следовательно, существует). Получим истинное числовое равенство f(а) = g(а). Это значит, что а – корень уравнения (1), т.е. а  Т₁, следовательно, Т₂  Т_1.

Т.к. Т₁  Т₂  Т₂  Т₁  Т₁ = Т₂, т.е. уравнения (1) и (2) равносильны на множестве Х.

Следствие. Если обе части уравнения умножить (или разделить) на одно и то же число, отличное от нуля, то получим уравнение, равносильное данному.

Теорема 3. Пусть уравнение f(x) = g(x) задано на множестве Х, f(x)  0, g(x)  0 на множестве Х и п – четное натуральное число. Тогда уравнения f(x) = g(x) и f ^п(x) = g^п(x) равносильны.

Другими словами: при возведении обеих частей уравнения в четную степень получается уравнение, равносильное данному при условии, что обе части уравнения неотрицательны.

Замечание. Если обе части уравнения возвести в четную степень, то полученное уравнение будет следствием исходного. Если п нечетное натуральное число, то уравнения f(x) = g(x) и f ^п(x) = g^п(x) равносильны.

Пример. Равносильны ли уравнения?

1. (4х + 3) ∙ х = 11х и 4х + 3= 11. Нет, т.к. мы разделили обе части уравнения на х, т.е. умножили на выражение 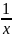, но при х = 0 оно не имеет смысла, т.е. мы не выполнили условие теоремы 2. Т₁ = {0; 2}, Т₂ = {2}.

2. (4х + 3)(х² + 2) = 11х и 4х + 3= 11 равносильны, т.к. х² + 2  0 ни при каких действительных х.

В начальном курсе математики теоретической основой решения уравнения является взаимосвязь между компонентами и результатом действий.