Применение теории активированного комплекса для расчета константы скорости химической реакции

I. Теоретическое введение

Теория активированного комплекса (ТАК) рассматривает химическую реакцию как движение системы по поверхности потенциальной энергии (ППЭ) вдоль пути реакции. На этом пути существует точка с максимальной энергией – вершина активационного барьера. Например, мономолекулярная химическая реакция

А = В

в ТАК выглядит как последовательное превращение:

, (1)

где A^ – переходное состояние (ПС) или активированный комплекс (АК). АК – это конфигурация атомов исходных веществ, соответствующая на ППЭ вершине активационного барьера для данной реакции. Предполагается, что АК находится в равновесии с реагентами ( – константа равновесия), а скорость реакции равна скорости распада АК ( – константа скорости распада).

Если участники реакции – идеальные газы, ТАК даёт следующее выражение для константы скорости мономолекулярной химической реакции k:

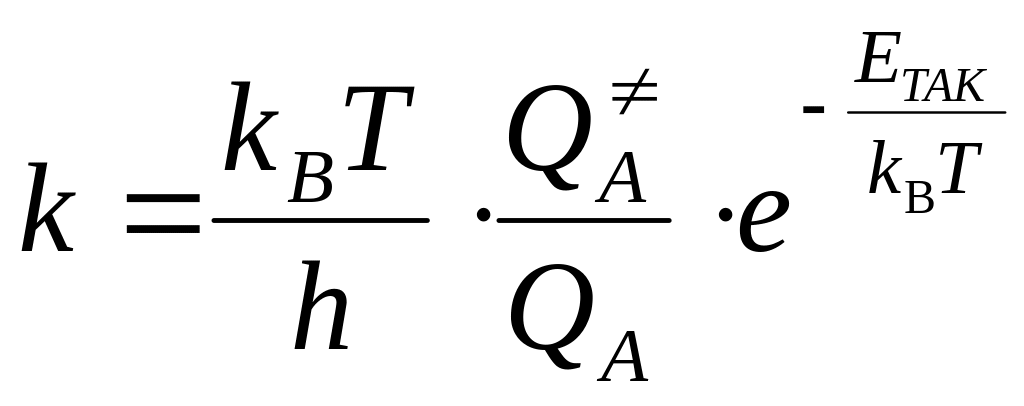, (2)

где Q^_A, Q_A – молекулярные суммы по состояниям активированного комплекса и реагента соответственно, k_B, h – константы Больцмана и Планка соответственно (1,3810^-23 Дж/К; 6,6310^-34 Джс), Т – абсолютная температура, E_ТАК – энергия активации ТАК – разница энергий нулевых уровней АК и реагента:

. (3)

Формулы, подобные (1-3), могут быть записаны и для бимолекулярной реакции.

Уравнение (2) позволяет рассчитать абсолютное значение константы скорости химической реакции. Для этого нужно знать энергию активации E_ТАК и суммы по состояниям Q^_A, Q_A.

Напомним, что молекулярная сумма по состояниям АК Q^_A представляет собой произведение поступательной, вращательной, колебательной и электронной сумм по состояниям. Для расчёта этих сумм нужно знать молекулярные параметры АК (массу, моменты инерции, частоты колебаний, вырожденность основного электронного уровня). Особенность активированного комплекса заключается в том, что в нем одна колебательная степень свободы заменяется дополнительной степенью свободы поступательного движения вдоль пути реакции. Эта колебательная степень свободы в АК соответствует колебанию по направлению разрываемой или образующейся в ходе химической реакции связи. Формально частота такого колебания является мнимой величиной.

Определение сумм по состояниям для реагентов не составляет труда.

Подробно теория активированного комплекса изложена в учебниках и монографиях [1, 2].

Современные методы расчета ППЭ и свойств АК

Теория активированного комплекса возникла в 20-е годы прошлого века. Однако, возможности расчета ППЭ и определения параметров АК для умеренно сложных реакций появились только в последние годы благодаря развитию методов квантовой химии и прогрессу компьютерной техники.

ППЭ молекулы можно определить как непрерывную функцию ее потенциальной энергии от всех независимых ядерных координат. В качестве ядерных координат R_i можно выбрать любые геометрические параметры молекулы, например, координаты атомов, расстояния между атомами или торсионные углы и т.п. Нам предстоит рассмотреть мономолекулярную реакцию изомеризации. Большинство молекул может существовать в виде нескольких изомеров, каждому из которых соответствует минимум на ППЭ. Переход из одного минимума в другой возможен только через энергетический барьер, так называемую седловую точку на ППЭ. Такой переход на ППЭ моделирует мономолекулярную реакцию изомеризации. На вершине барьера молекула принимает конфигурацию АК.

Рассмотрим, как можно рассчитать энергию активации и константу скорости данной реакции. Задача будет решена, если удастся построить ППЭ всей системы атомов. Однако, количество независимых ядерных координат весьма велико. Для молекулы бутана (С₄Н₁₀), например, оно равно 143–6=36. Если ограничить варьирование каждой внутренней координаты всего 10 точками (например, для длины связи С–С это может быть от 1,35 до 1,8 Å с шагом 0,05 Å), расчет энергии придется проводить 10³⁶ раз. Пусть расчет одной структуры будет занимать всего 1 с. Тогда получение всей ППЭ потребует 10²⁸ лет. Ясно, что подобный метод не может использоваться в практической работе. Реально можно построить путь реакции на ППЭ, иначе, сечение ППЭ по координате реакции. Координата реакции – это какой-либо геометрический параметр системы, позволяющий следить за движением фигуративной точки на ППЭ вдоль пути реакции от реагентов к продуктам через активационный барьер (седловую точку). Для рассматриваемой реакции изомеризации сечение ППЭ по координате реакции схематично выглядит так:

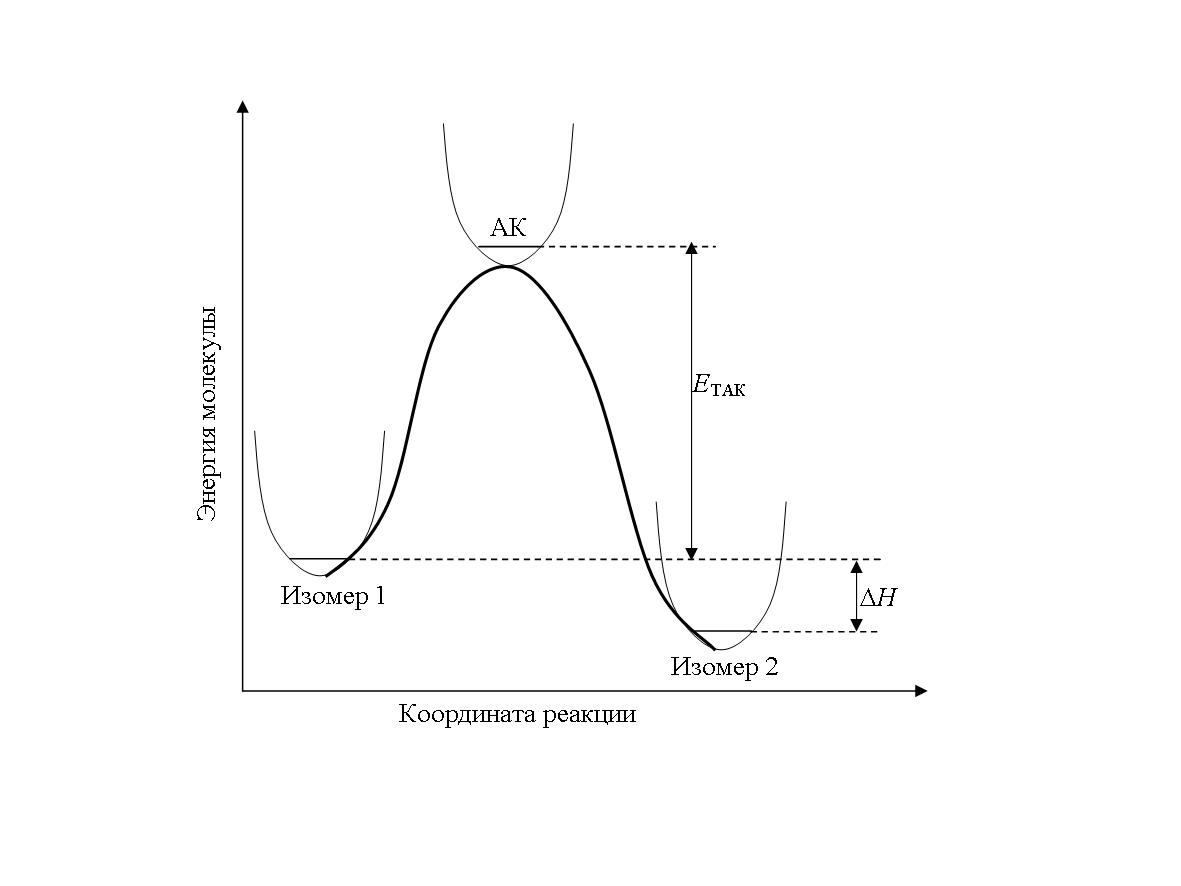
Расчет подобных сечений ППЭ проводится следующим образом. Сначала выбранным методом квантовой химии рассчитывают структуру и полную энергию реагента (Изомер 1) и продукта (Изомер 2), минимизируя значение энергии. Процедура поиска минимума на ППЭ называется оптимизацией геометрии. В большинстве современных пакетов программ для проведения квантово-химических расчетов имеются специальные процедуры оптимизации геометрии к стационарной точке. Стационарная точка может соответствовать минимуму энергии на ППЭ или быть седловой. Необходимо установить, к какому из двух типов точек привела нас процедура оптимизации.

В курсе «Строение молекул» было показано, что в стационарных точках на ППЭ производные полной энергии Е системы по всем независимым координатам R_i равны нулю:

. (4)

Матрица вторых производных энергии по всем независимым координатам, составленная из элементов,

(5)

называется Гессианом.

Для того, чтобы установить, соответствуют ли структуры минимуму на ППЭ или седловой точке, необходимо найти собственные значения Гессиана. Напомним из курса «Линейной алгебры», что собственными значениями матрицы А являются числа , для которых существует ненулевой вектор х такой, что Ах = х, вектор х называют собственным вектором. Собственный вектор матрицы вторых производных энергии описывает колебательное движение каждого атома вдоль нормальной координаты, а собственные значения Гессиана связаны с колебательными частотами молекулы _i следующим уравнением:

. (6)

В точке минимума на ППЭ матрица вторых производных имеет только положительные собственные значения (все частоты колебаний – действительные числа). В седловой точке среди положительных значений появляется одно отрицательное собственное значение, и, следовательно, появляется мнимая частота колебания (корень квадратный из отрицательного числа, см. уравнение (6)). Структура является неустойчивой по отношению к смещениям, соответствующим данному колебанию.

Минимумы полной энергии соответствуют устойчивым структурам, а седловые точки – переходным состояниям (АК).

Так как АК не является минимумом на ППЭ, поиск его структуры и расчет энергии представляет сложную и творческую задачу. Подчеркнем, что долгое время структуры переходных состояний невозможно было установить. Сегодня благодаря квантово-химическим методам определили структуру АК некоторых реакций. В будущем это, возможно, будет сделано экспериментально – методом фемтосекундной спектроскопии высокого разрешения [1]. Разработано много алгоритмов оптимизации геометрии к седловой точке. Преимущества и недостатки каждого квантово-химического метода оптимизации геометрии АК обычно описываются в инструкциях к квантово-химическим программам, в которых он реализован. Здесь представим только общий подход к решению задачи.

Задают стартовую геометрию АК исходя из структуры исходного вещества или продукта. Далее, имея предварительно рассчитанную матрицу вторых производных (Гессиан), проводят локализацию АК (см. раздел 2.1). Для этого минимизируют градиент – производную потенциальной энергии по независимой ядерной координате:

. (7)

Градиент дает направление, в котором энергия наиболее быстро уменьшается, и крутизну спуска. Точка минимума градиента отвечает координатам АК. Такой подход срабатывает лишь вблизи седловой точки и лишь в том случае, когда стартовая конфигурация АК задана удачно, т.е. «похожа» на его предполагаемую конфигурацию. Если АК по строению напоминает исходную молекулу, то говорят о раннем переходном состоянии, если продукт – о позднем.

После локализации АК необходимо провести его идентификацию, то есть убедиться, что найденная конфигурация АК соответствует нужной нам химической реакции (см. раздел 2.2). Для идентификации применяют метод IRC (Intrinsic reaction coordinate), позволяющий осуществить спуск из седловой точки к исходным веществам и продуктам вдоль пути реакции и проследить, как изменяется при этом геометрия системы. Проверяют, приводит ли реакция, проходящая через данный АК, к нужным реагентам и продуктам. Задание для расчетов методом IRC должно включать геометрию переходного состояния и Гессиан. Собственный вектор, соответствующий отрицательному собственному значению Гессиана, определяет координату реакции и направление спуска из седловой точки. Очевидно, что таких направлений должно быть два: в сторону исходных веществ (rel_1) и в сторону продуктов (rel_2). При каждом спуске по координате реакции сначала находится ближайший минимум, а затем отрезок от седловой точки до найденного минимума разбивается на заданное число точек (шагов). На каждом шаге рассчитывают значения координаты реакции в атомных единицах (bohrm^1/2) и соответствующие им значения энергии (см. окно на рис. 2, раздел 2.2).

Одновременно с вычислением энергии большинство квантово-химических программ рассчитывают все молекулярные постоянные, частоты колебаний и полные энергии при Т=0 К для реагента и активированного комплекса АК. Если сечение ППЭ уже построено, подобные расчеты не вызывают затруднений.

Энергия активации ТАК рассчитывается как изменение внутренней энергии в реакции превращения реагентов в АК при 0 К (см. уравнение 3). В правой части уравнения (3) стоят энергии молекулы-реагента и АК на основных колебательных уровнях. Эти величины можно получить, прибавив в обоих случаях к рассчитанным значениям полной энергии E энергию нулевых колебаний (ZPE):

E⁰ = E + ZPE,

где выражения для энергии нулевых колебаний ZPE определяются в приближении гармонического осциллятора:

.

Молекулярные постоянные для реагента и АК позволяют рассчитать суммы по состояниям для этих частиц. В результате, появляется возможность воспользоваться уравнением ТАК (см. уравнение 2) и определить значение константы скорости химической реакции (см. раздел 2.3).

Расчет энтальпии, энтропии и энергии Гиббса химической реакции

В курсе статистической термодинамики были получены формулы, связывающие термодинамические функции для индивидуальных веществ с их суммами по состояниям. Для идеальных газов возможен простой расчет сумм по состояниям на основании молекулярных параметров. Если известны термодинамические функции для продуктов и реагентов, можно рассчитать стандартные изменения внутренней энергии, энтальпии, энергии Гиббса для химической реакции [3].

Подобный расчет не имеет отношения к химической кинетике и теории активированного комплекса, однако, современные квантово-химические программы дают возможность провести такие вычисления одновременно с расчетом константы скорости по ТАК (см. раздел 2.3). При построении сечения ППЭ вдоль координаты реакции автоматически рассчитываются молекулярные параметры и внутренние энергии при 0 К для продуктов и реагентов. Этих данных достаточно для того, чтобы рассчитать химической реакции при любой температуре Т.