Электроника

(Конспект курса лекций)

№№ п.п.	Наименование темы (раздела)	Часов по разделам
		Лекции	Лаборат. работы	Самост. работа
1.	Введение.	0,25
2.	Физические основы полупроводниковой электроники.	3
3.	Контактные явления в полупроводниках.	5
4.	Полупроводниковые диоды.	4	4
5.	Биполярные транзисторы.	10	12
6.	Полевые транзисторы.	4	12
7.	Полупроводниковые приборы с отрицательным дифференциальным сопротивлением.	4
8.	Полупроводниковые фотоэлектрические и излучающие приборы.	2
9.	Электронные индикаторные приборы.	1
10.	Оптоэлектронные приборы.	2	4
11.	Долговечность надёжность и экономичность полупроводниковых приборов.	0,5
12.	Шумы электронных приборов.	2
13.	Микроэлектроника. История, состояние, тенденции.	2
14.	Технологические основы микроэлектроники.	4
15.	Элементы интегральных микросхем.	6
16.	Приборы с зарядовой связью.	2	4
17.	Введение в функциональную электронику.	2
18.	Заключение	0,25
Всего часов:		54	36	80

Литература

№№	Авторы	Наименование	Год	Кол
Основная
1.	Пасынков В.В. Чиркин Л.К.	Полупроводниковые приборы	1987
2.	Тугов Н.М. и др.	Полупроводниковые приборы	1990
3.	Степаненко И.П.	Основы теории транзисторов и транзисторных схем	1987
4.	Свешников С. В.	Элементы оптоэлектроники	1971
5.	Степаненко И.П.	Основы микроэлектроники	1980
Дополнительная
6.	Жеребцов И.П.	Основы электроники	1990
7.	Шалимова К.В.	Физика полупроводников	1985
8.	Ефимов И.Е.	Микроэлектроника	1986
9.	Батушев В.А.	Электоронные приборы	1980
10.	Дудин В.Н.	Электронные приборы	1977
11.	Головатенко-Абрамова М.П. Лапидес А.М.	Задачи по электронике	1992

ВВЕДЕНИЕ

Процесс совершенствования радиоэлектронной аппаратуры неразрывно связан с развитием

и совершенствованием её элементной базы. За каждое десятилетие число элементов в аппаратуре

увеличивается в 5-20 раз, что связано с усложнением требований и задач решаемых современными

радиосистемами.

_i = qn_i(_n + _p) чтобы определить проводимость собственного полупроводника надо знать лишь концентрацию носителей заряда n_i, заряд электрона q = 16*10^-20 Кулон, а подвижности носителей заряда _n и _p определяются материалом полупроводника. Из за того, что при температуре отличной от нуля, по Кельвину узлы кристаллической решётки испытывают хаотические колебания, говорить о том, что валентный электрон, имеющий в данный момент времени некоторую энергию получит её приращение имеющее заранее известное (детерминированное) значение, не имеет смысла. Поэтому

судить о том, сколько электронов, при данной температуре полупроводника, будет в состоянии покинуть валентную зону и оказаться в зоне проводимости, можно лишь вероятностно.

Вероятность заполнения электроном энергетического уровня с энергией W, при заданной температуре T, количественно выражается функцией распределения Ферми-Дирака:

F_n(W) = 1/(1 + exp((W - W_F) / kT ))

где k – постоянная Больцмана, T – абсолютная температура. W_F – носит название уровня Ферми.

Очевидно, что могут иметь место лишь два события – либо данный энергетический уровень занят электроном, либо не занят ( т.е. он занят дыркой). Эти два события составляют полную группу, следовательно если обозначить через F_p(W) вероятность нахождения дырки на энергетическом уровне W, то можем записать F_n(W) + F_p(W) = 1. Т.е. F_p(W) = 1 - F_n(W), или

F_p(W) = 1/(1 + exp((W_F - W) / kT )).

В еличина W_F, входящая в выражение, называется энергией или уровнем Ферми, который может быть определён как энергетический уровень равновероятный как для электрона, так и для дырки.

При T=0 функция Ферми превращается в ступенчатую.

ПОЯСНИТЬ ХОД КРИВЫХ!!!

Для собственного полупроводника уровень Ферми лежит в середине запрещённой зоны, т.к. функция вероятности симметрична относительно него при любой фиксированной температуре.

Заметим, что функция Ферми имеет

смысл только в валентной и запрещённой зонах, т.к. в запрещённой зоне носители заряда находиться не могут. Воспользуемся статистикой Ферми-Дирака для определения концентрации электронов и дырок в собственном полупроводнике. Учтём, что энергетические уровни зоны проводимости, а также и валентной зоны распределены неравномерно, т.е. их плотность зависит от энергии.

Число энергетических уровней в зоне проводимости, попадающих в единичный, бесконечно малый энергетический интервал dW, обозначим через функцией P(W), которая будет характеризовать плотность энергетических уровней. Тогда количество электронов, занимающих разрешённые энергетические уровни в некоторой полосе dW определяется числом уровней dW·P(W) в этой элементарной полосе и вероятностью их заполнения F_n(W). Т.е. dn_i = P(W)·F_n(W)·dW.

Полное число электронов, приходящихся на 1 см³ вещества и занимающих энергетические уровни в полосе энергий от W₁ до W₂ будет равно:

А налогичным образом для концентрации дырок валентной зоны получим:

В обоих случаях интегрирование ведётся по всей ширине зоны проводимости (сonductivity) или валентной (valency) зоны. В результате интегрирования можно придти к следующим выражениям:

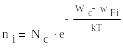
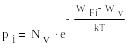
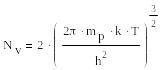
где:

N_c-эффективная плотность состояний (на 1см³) в зоне проводимости и валентной зоне

соответственно.

h = 4,14·10^-15 эв·сек – постоянная Планка. m_n и m_p – эффективная масса электрона и дырки соответственно. * Эффективная масса электрона определяется из уравнения F = m_n ·dV/dt, где

F – сила, действующая на электрон, а V – скорость электрона.

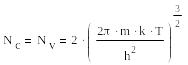В большинстве практических случаев можно считать, что m_n = m_p = m – массе электрона в состоянии покоя. Тогда:

П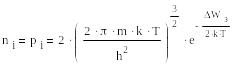 оложив далее, что ΔW_з = W_c -W_v и учитывая, что n_i = p_i , выражения для концентрации электронов и дырок можно привести к виду:

При этих условиях уровень Ферми лежит точно посередине запрещённой зоны, т.е. W_Fi = (W_с-W_v) / 2.

Подставляя найденное значение концентрации n_i в выражение для проводимости собственного полупроводника придем к след. зависимости:

К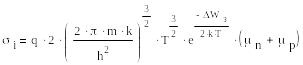 ак правило ΔW_з >> k·T, подвижности зарядов μ_n и μ_p

мало зависят от температуры, а экспонента растёт гораздо быстрее, чем T^3/2 . Поэтому с достаточной для

п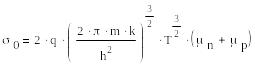 рактики точностью можно считать, что:

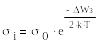
где:

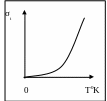
Из последних выражений и рисунка видно, что зависимость удельной проводимости собственного полупроводника от температуры носит сугубо нелинейный характер и близка к экспоненциальной.