Позиционные задачи

Это задачи графического определения положения геометрических фигур относительно плоскостей проекций и взаимного положения геометрических фигур (принадлежность, параллельность, пересечение, касание как частный случай пересечения).

Пересечение геометрических фигур

Задача сводится к нахождению проекций общих точек для пересекающихся фигур.

Общий для всех этих задач прием графического построения – введение вспомогательных поверхностей γ_i. Затем строят фигуры пересечения Ф_1i и Ф_2i вспомогательных поверхностей γ_i с заданными фигурами. Общие точки для заданных пересекающихся фигур получают при пересечении Ф_1i и Ф_2i.

Выбор вспомогательных поверхностей γ_i определяется из условия, чтобы проекции линий пересечения заданных фигур и вспомогательной поверхности были по возможности простыми. Теоретически целесообразно использовать такие вспомогательные поверхности, которые пересекают заданные поверхности по семействам направляющих или образующих заданных пересекающихся поверхностей.

Надо отметить, что использование вспомогательных проецирующих плоскостей всегда дает решение и чаще всего применяется на практике. В некоторых случаях использование других вспомогательных поверхностей (сфер, плоскостей общего положения и т.д.) дает более удобные графические построения.

Когда одна из двух пересекающихся фигур занимает проецирующее положение, т.е. перпендикулярна плоскости проекций (таких фигур три: прямая, плоскость, цилиндрическая поверхность), то вспомогательные поверхности не используют, а используют свойства проецирующей фигуры.

В данном курсе рассмотрим использование вспомогательных проецирующих плоскостей.

1. Пересечение прямой линии с поверхностью

Пересечение прямой линии с плоскостью

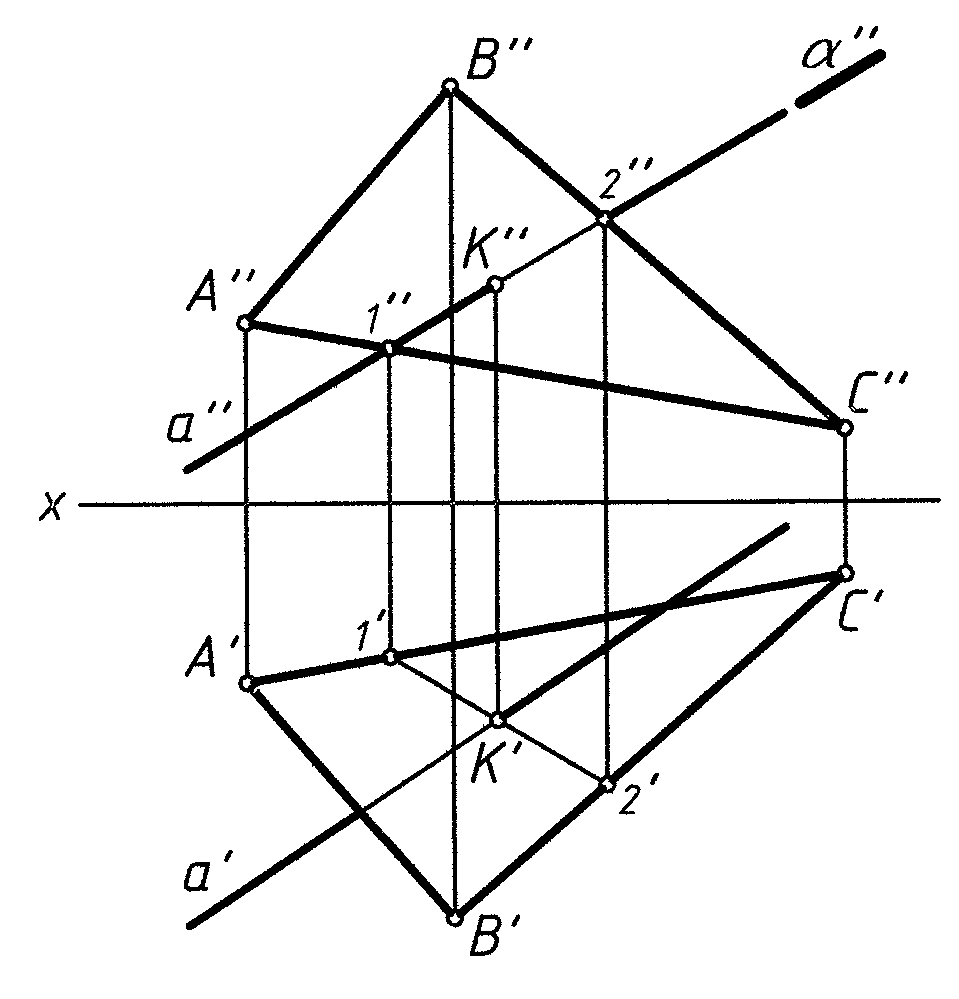Общий случай (рис. 1)

Рис. 1

Последовательность построения:

1. Вводим вспомогательную проецирующую плоскость α (α _┴ π₂ в данном случае), в которую заключаем прямую a;

2. α ∩ ∆ABC → (1 - 2);

3. (1 - 2) ∩ a → K, т.к. прямая a и прямая (1 - 2) лежат в одной плоскости α и (1 - 2) принадлежит ∆ABC.

Частные случаи (рис. 2, 3, 4)

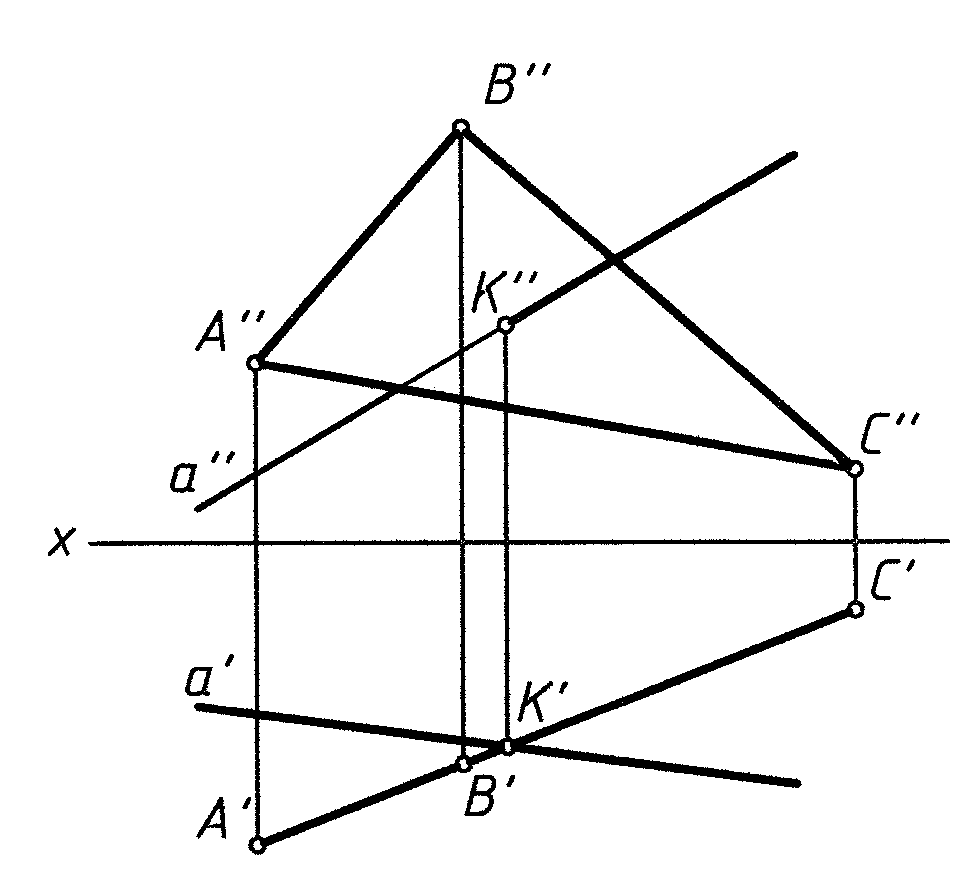
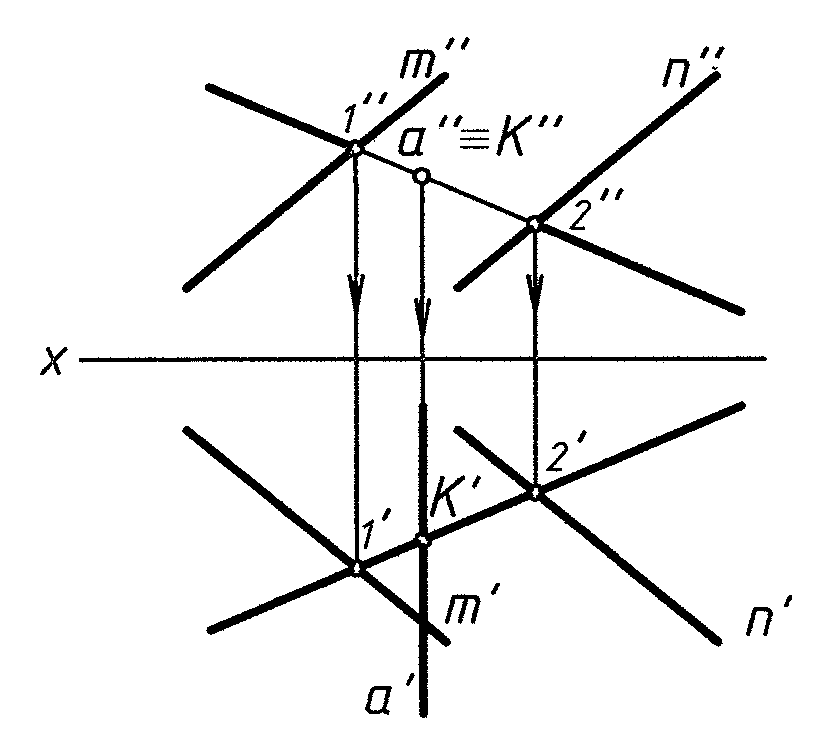
прямая проецирующая плоскость проецирующая прямая проецирующая и плоскость проецирующая

Рис. 2 Рис. 3 Рис. 4

При проецирующем положении прямой или плоскости задачи сводятся к нахождению проекции точки, лежащей в плоскости, или точки, принадлежащей прямой.

2. Пересечение прямой линии с поверхностью вращения

Общий случай (рис. 5)

Последовательность построения аналогична задаче пересечения прямой с плоскостью:

1) α - вспомогательная проецирующая плоскость;

2) ;

3) α ∩ поверхностью → кривая (1 – 3 – 2);

4) кривая (1 – 3 – 2) ∩ a → K₁; K₂.

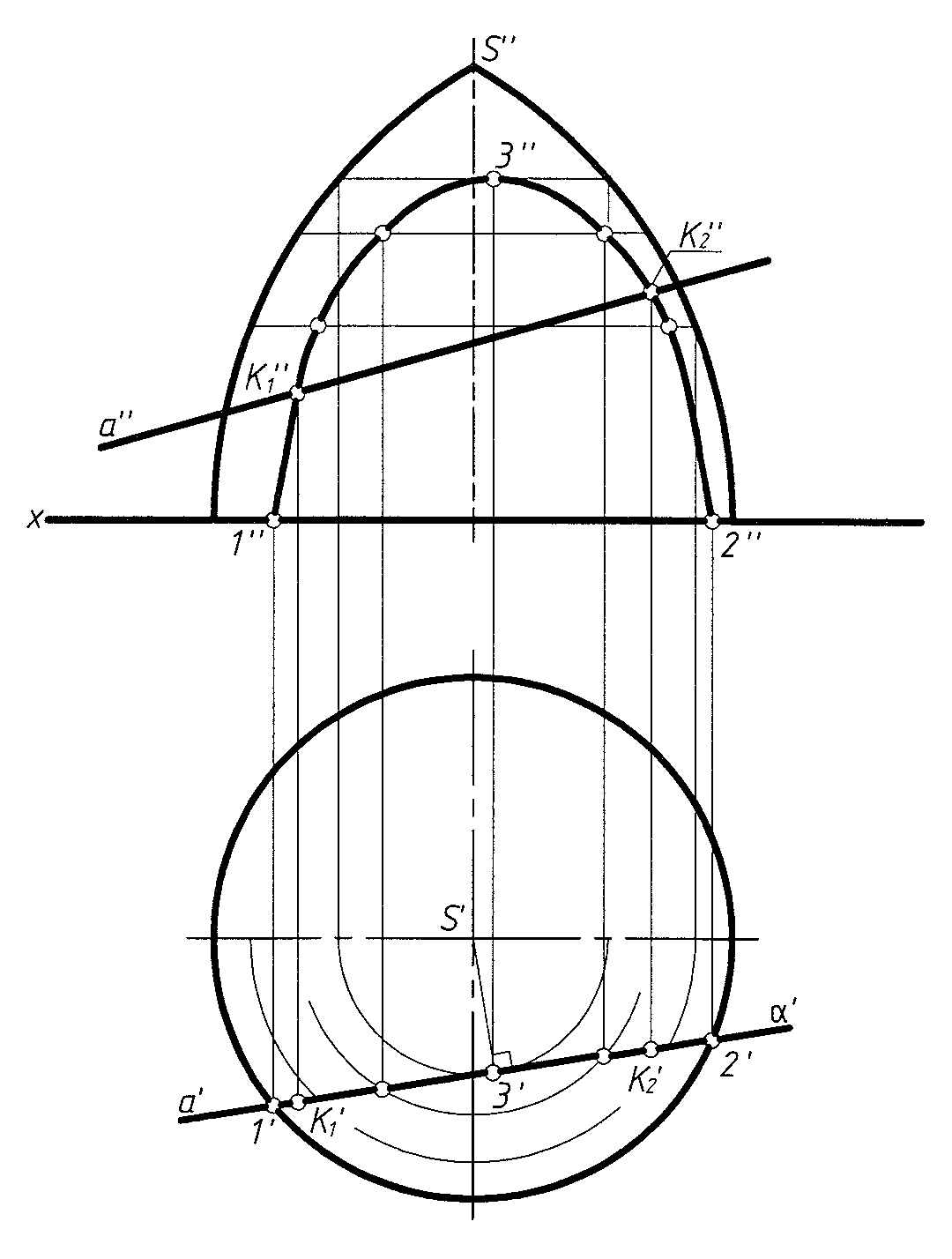
Рис. 5

Частные случаи

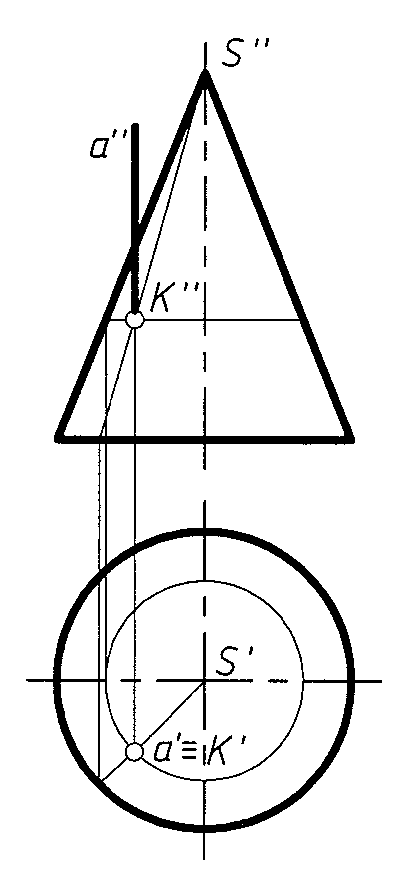
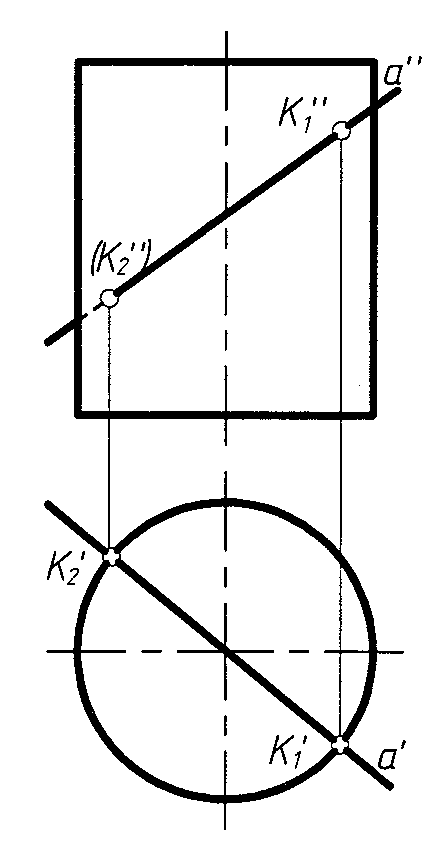
Р 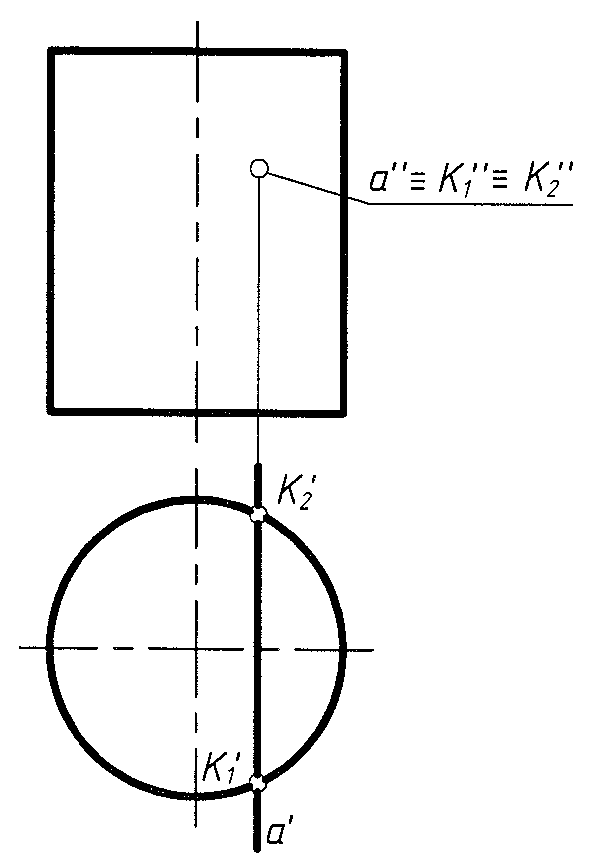ис. 6 – прямая – проецирующая; рис. 7 – поверхность – проецирующая; рис. 8 – прямая и – поверхность – проецирующие.

Рис. 6 Рис. 7 Рис. 8

3. Пересечение поверхностей

Общий случай

План решения

α ∩ β → l₁, l₂ …

вводим ɣ_i – вспомогательные поверхности;

α ∩ γ_i → m_i; β ∩ γ _i → n_i;

m_i ∩ n_i (т.к. лежат в одной поверхности γ_i)

m_i ∩ n_i → K_i;

4. K₁ K₂ K₃ … K_i → l_i

Используем вспомогательные проецирующие плоскости (чаще всего в инженерной практике используются плоскости уровня) (рис. 9).

Начинаем построения с характерных точек – (1, 3, 2).

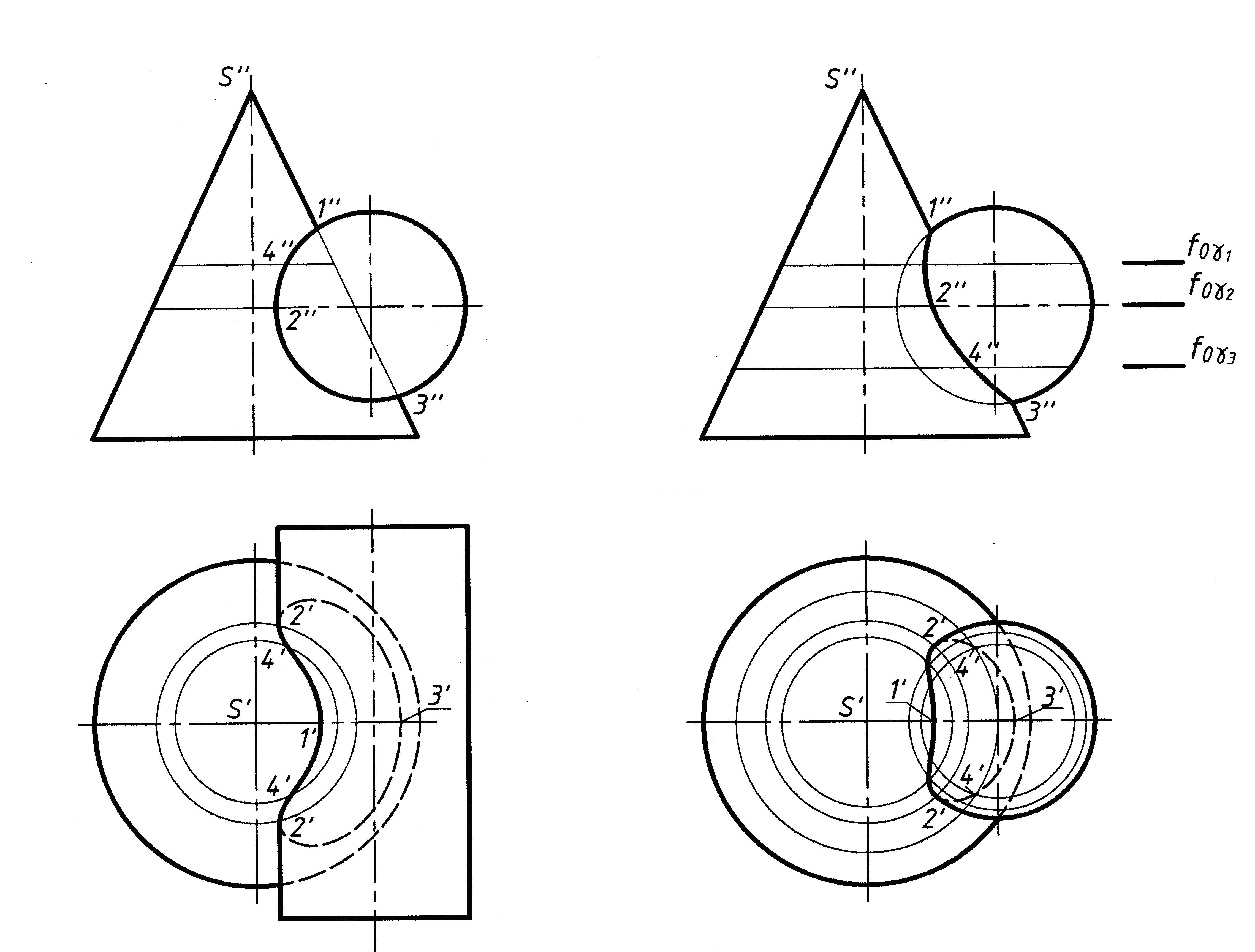
Рис. 9

Если одна из двух пересекающихся поверхностей проецирующая цилиндрическая, то вспомогательные поверхности не используют, а используют проецирующее свойство цилиндрической поверхности (рис. 10). Проекции точек строят с помощью окружностей (или образующих), принадлежащих конической поверхности.

Рис. 10