Поверхности вращения

П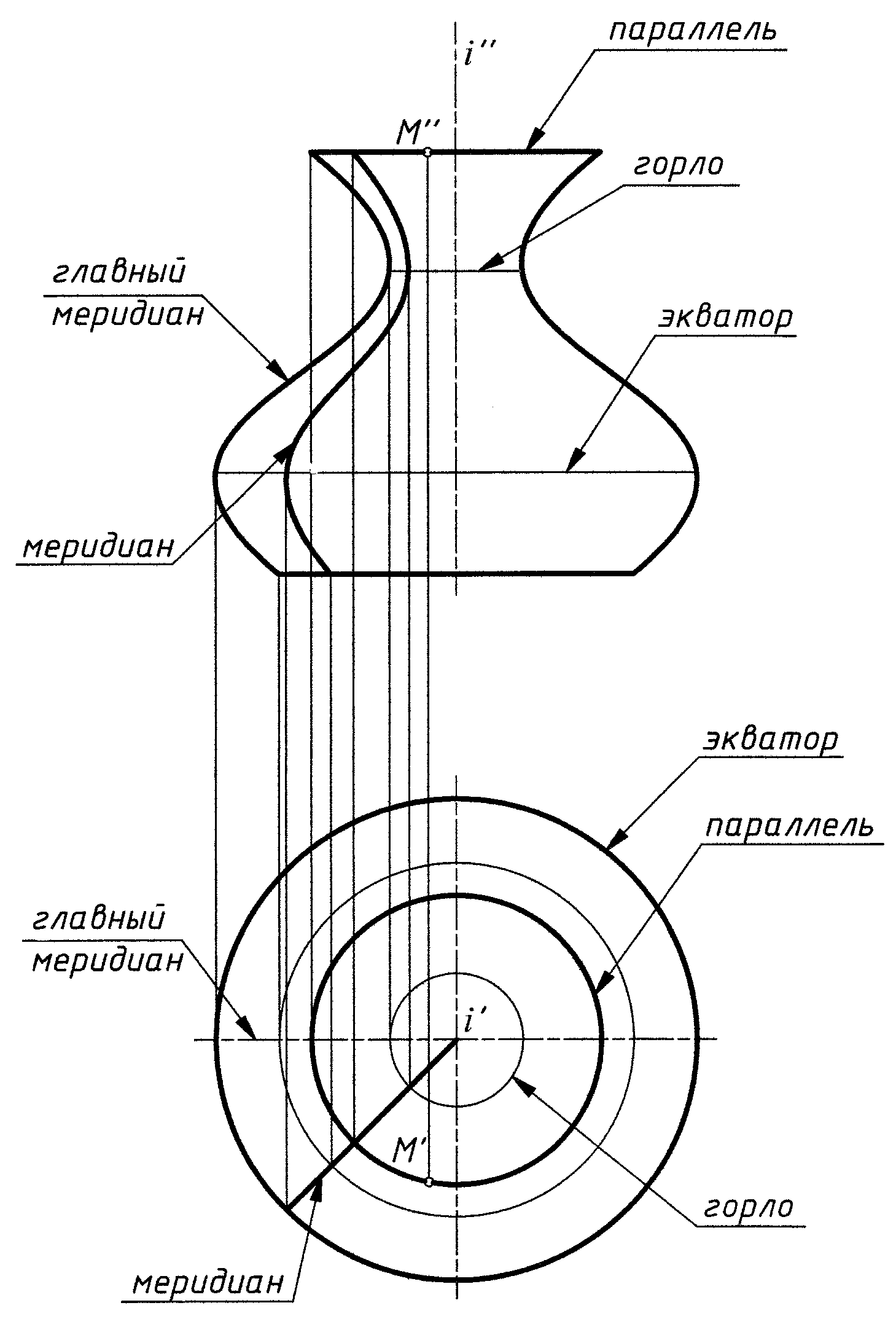 оверхностью вращения называется поверхность, образованная вращением линии (образующей) вокруг некоторой неподвижной прямой (оси вращения).

Общий случай (рис. 8)

Рис. 8

Параллели – окружности - в плоскости, перпендикулярной оси вращения i.

Меридианы – в плоскости, проходящей через ось i.

Параллели и меридианы образуют каркас поверхности вращения.

Обычно ось i располагают перпендикулярно плоскости проекций (например, перпендикулярно π₁).

Если ось поверхности i перпендикулярна π₁ , то главный меридиан – очерк на фронтальной плоскости проекций, а экватор – очерк на горизонтальной плоскости проекций.

Построить проекции точки, принадлежащей поверхности вращения, можно всегда с помощью параллели (см. рис. 8 – точка M(M′, M″)).

Простейшие поверхности вращения и соответствующие им тела вращения

Цилиндр – цилиндрическая поверхность, ограниченная двумя плоскостями

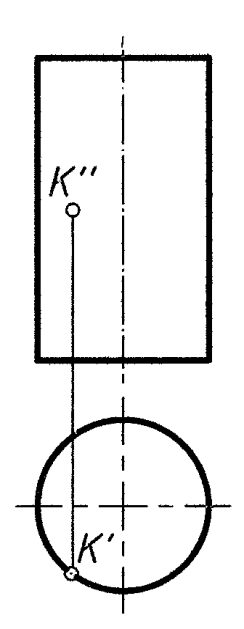
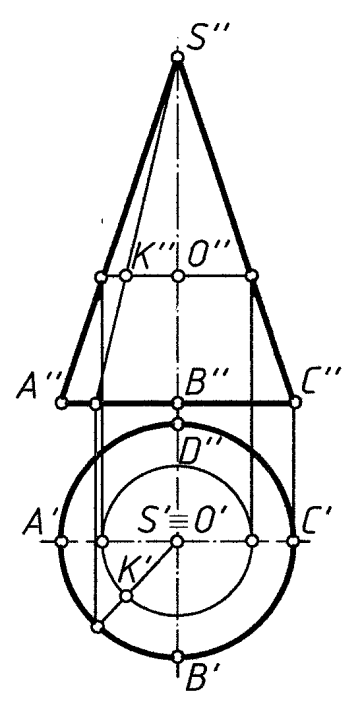
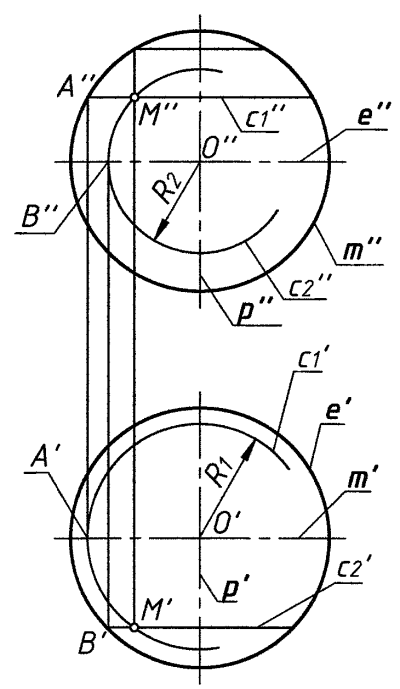( рис. 9).

Рис. 9 Рис. 10 Рис. 11

Цилиндрическая поверхность обладает проецирующим свойством, если образующая перпендикулярна плоскости проекций.

Конус – коническая поверхность, ограниченная одной (двумя) плоскостями (рис. 10).

Показаны проекции точки K (K′, K′′), принадлежащей цилиндрической и конической поверхностям.

На рис. 11 представлена сфера.

Показаны проекции (M′, M′′) точки M, принадлежащей сфере.

Лекция №5(ИУ1, 2, 4);№6(ИУ3, 8, 5, 6)

1. Пересечение тел вращения проецирующей плоскостью Цилиндр

На рис. 1 дано построение проекций цилиндра, усеченного фронтально-проецирующей плоскостью γ, наклоненной к оси цилиндра под углом α°.

Рис. 1

Плоскость γ пересекает поверхность цилиндра по эллипсу, который проецируется:

- на фронтальную плоскость проекций в отрезок прямой, заключенный между очерковыми образующими и совпадающий с проекцией плоскости γ. Этот отрезок равен действительной длине большой оси эллипса. Центр эллипса (точка О) находится в середине большой оси и на пересечении оси вращения цилиндра с плоскостью эллипса. С точкой О" совпадает фронтальная проекция малой оси эллипса, равная диаметру цилиндра;

- на горизонтальную плоскость проекций – в окружность, так как поверхность цилиндра является проецирующей;

- на профильную плоскость проекций в эллипс, центр которого и большая ось (для заданного положения плоскости γ по отношению к оси цилиндра) построены с помощью горизонтальных линий связи. Малая ось эллипса равна диаметру цилиндра.

На рис. 1 построен истинный вид эллипса на дополнительной плоскости, параллельной плоскости γ.

На рис. 2 даны построения проекций цилиндра со сквозными отверстиями.

Прямоугольное сквозное отверстие на рис. 2, а ограничено двумя вертикальными и двумя горизонтальными плоскостями. Вертикальные боковые плоскости пересекают цилиндр по образующим. Горизонтальные плоскости отверстия пересекают цилиндрическую поверхность по дугам окружностей. На фронтальной и профильной проекциях дуги окружности проецируются в отрезки прямых линий. Горизонтальная проекция дуг совпадает с окружностью, в которую проецируется поверхность цилиндра.

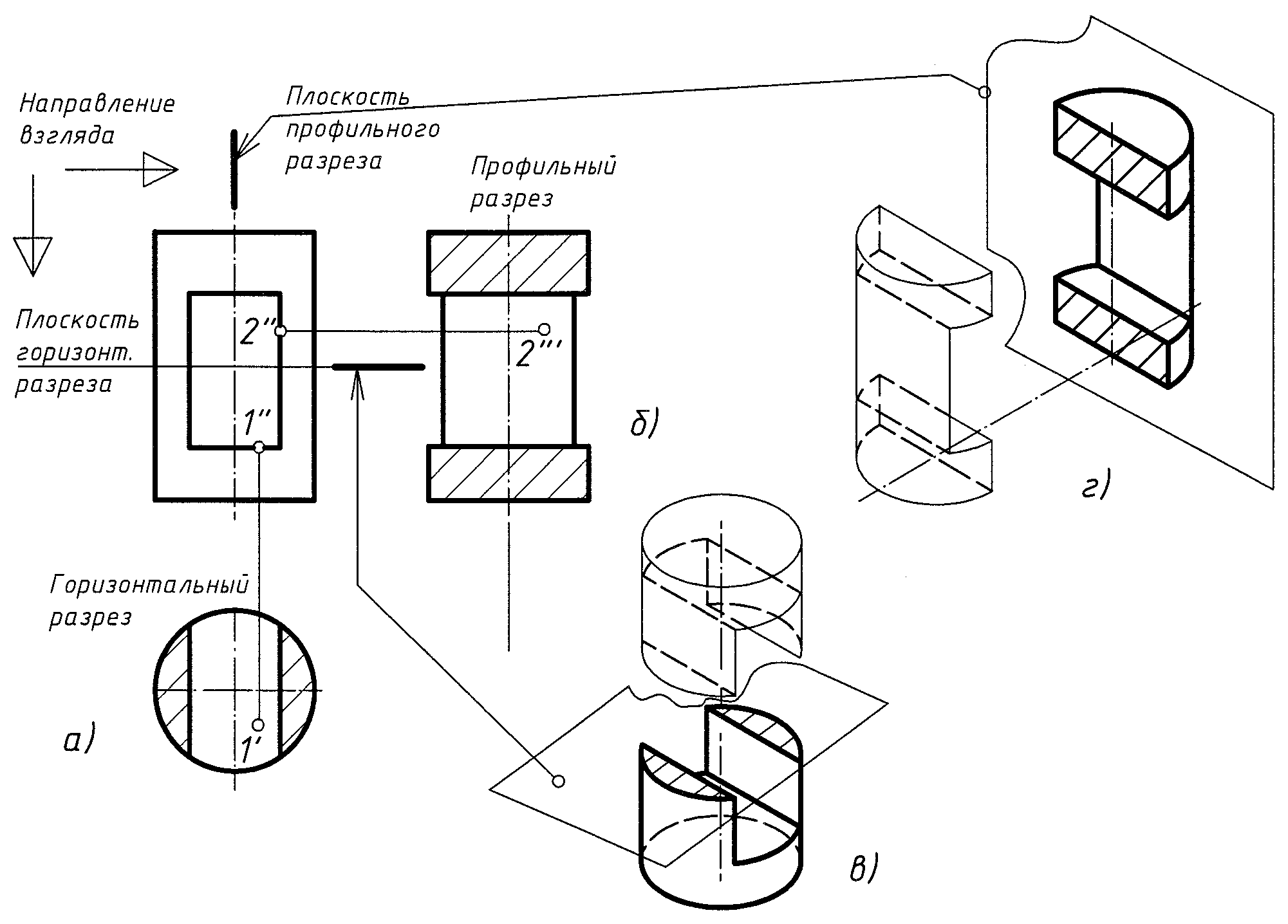
Рис. 2

Сквозное отверстие вырезает часть боковой поверхности цилиндра, поэтому очерк фигуры на профильной плоскости проекций изменяется, приобретая вид ломаной линии.

Чтобы сделать видимыми внутренние поверхности цилиндра с прямоугольным сквозным отверстием, на рис. 2 выполнены два разреза: горизонтальной и вертикальной (профильной) плоскостями. Стрелками указано направление взгляда.

На горизонтальном разрезе (рис. 2, а, в) стала полностью видимой нижняя горизонтальная плоскость сквозного отверстия. Точки 1' и 1" являются горизонтальной и фронтальной проекциями точки 1, лежащей на этой плоскости. Часть цилиндра, расположенную выше плоскости горизонтального разреза, мысленно удаляют. Заштрихована фигура, по которой плоскость разреза разделила удаленную и оставшуюся части цилиндра.

На профильном разрезе (рис. 2, б, г) стала видимой правая боковая плоскость отверстия. Точки 2" и 2''' являются фронтальной и профильной проекциями точки 2, принадлежащей этой плоскости. Половину цилиндра, расположенную перед плоскостью профильного разреза, мысленно удаляют. На профильном разрезе заштрихованы прямоугольники, по которым произошло разделение удаленной и оставшейся частей цилиндра.

Оба разреза построены независимо друг от друга как для целого цилиндра.

Конус

Секущая плоскость не проходит через вершину конуса S (рис. 3)

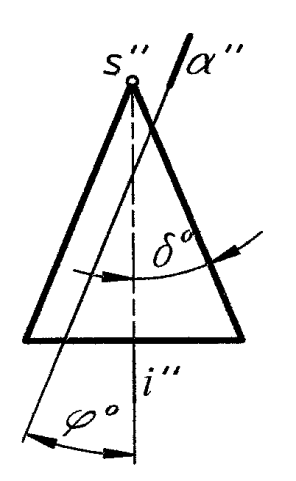
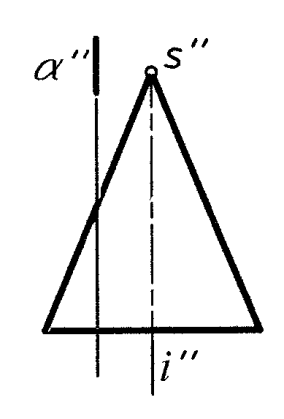
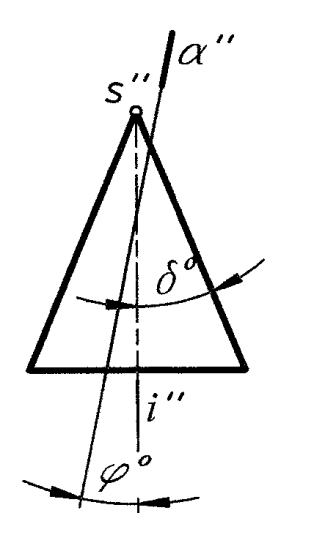
i > δ = δ < δ = 0; α|| i

окружность эллипс парабола гипербола равносторонняя

гипербола

Рис. 3

Секущая плоскость проходит через вершину конуса S (рис. 4).

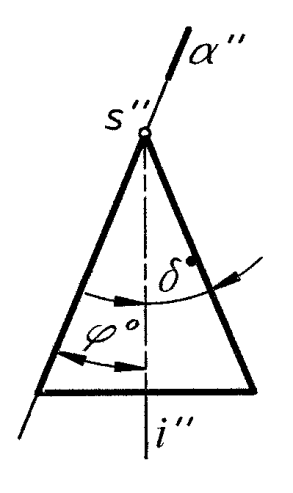
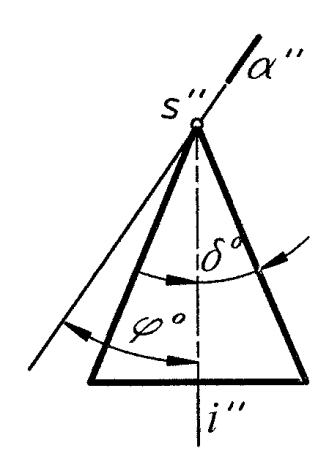
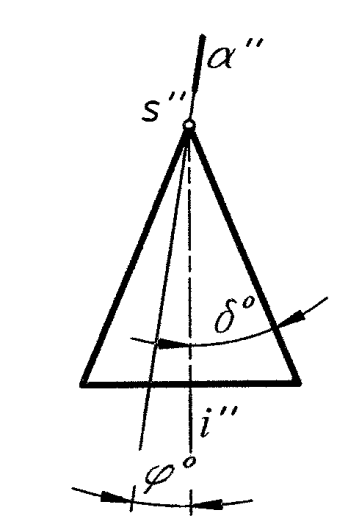
= δ > δ

Две прямые (образующие) одна прямая (образующая) точка – вершина S

Рис. 4

На рис. 5 показаны примеры построения пересечения конуса плоскостями

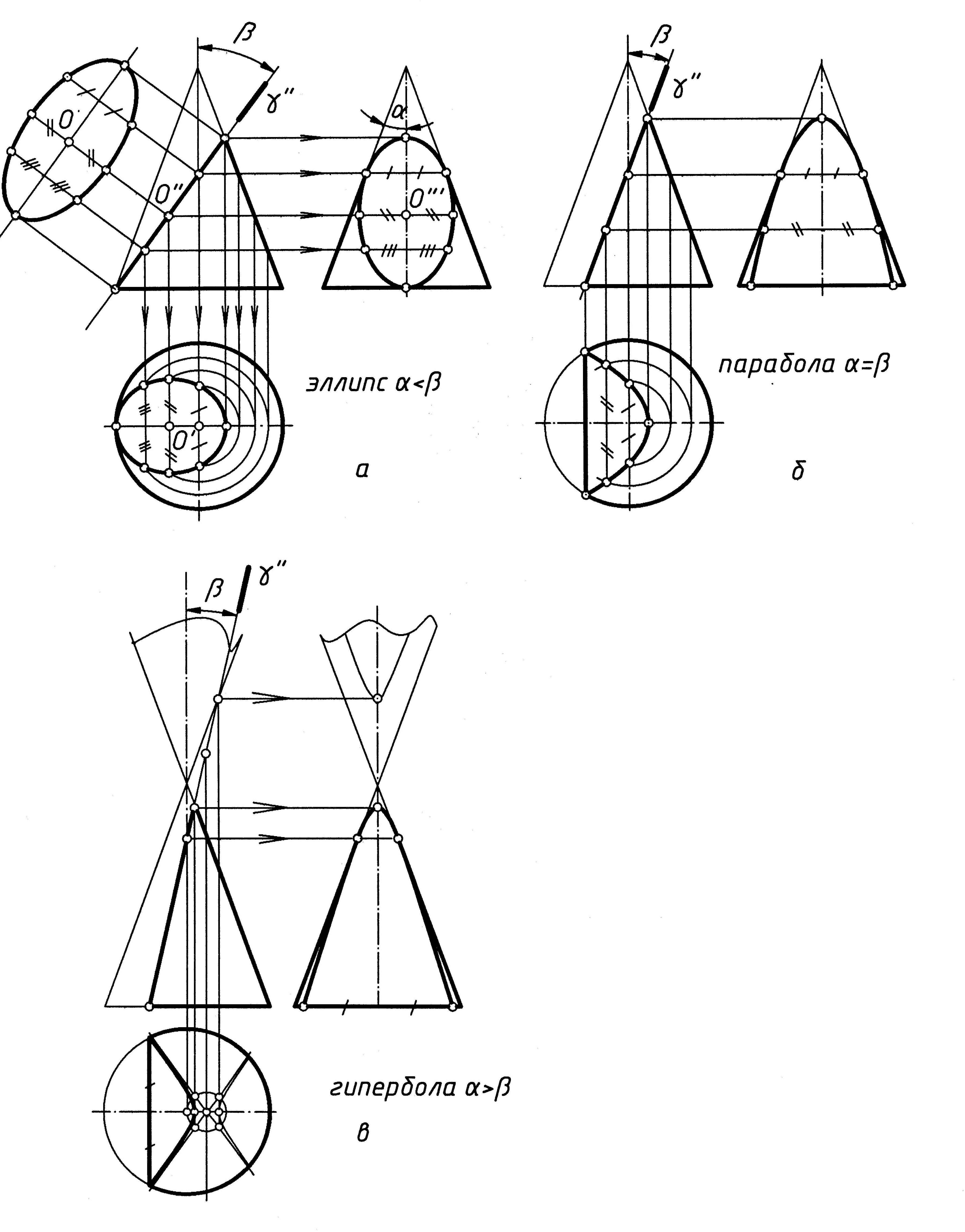
Рис. 5

На рис. 5, а, б, в построены проекции трех одинаковых конусов вращения с образующей, наклоненной к оси под углом α. Конусы усечены фронтально-проецирующими плоскостями γ, не проходящими через вершину и составляющими с осью угол наклона β. На трех рисунках конуса углы β имеют разную величину:

– если α < β, то в сечении конуса плоскостью γ получится эллипс (рис. 5, а);

– если α = β, сечением конуса плоскостью γ будет парабола (рис. 5, б);

– если α > β, плоскость γ рассечет конус по гиперболе (рис. 5, в).

Истинный вид эллипса на дополнительной плоскости, параллельной плоскости γ, построен на рис. 5, а. На фронтальную плоскость проекции эллипс проецируется в отрезок прямой, заключенный между очерковыми образующими конуса. Центр эллипса О (О', О",О''') находится в середине этого отрезка. С точкой О" совмещается фронтальная проекция малой оси эллипса. Действительная величина малой оси эллипса и другие промежуточные точки, принадлежащие эллипсу, построены с помощью параллелей конуса. Полученные координаты Y точек на горизонтальной плоскости использованы для построения истинного вида эллипса.

Построение проекций конуса со сквозным отверстием показано на рис. 6, а.

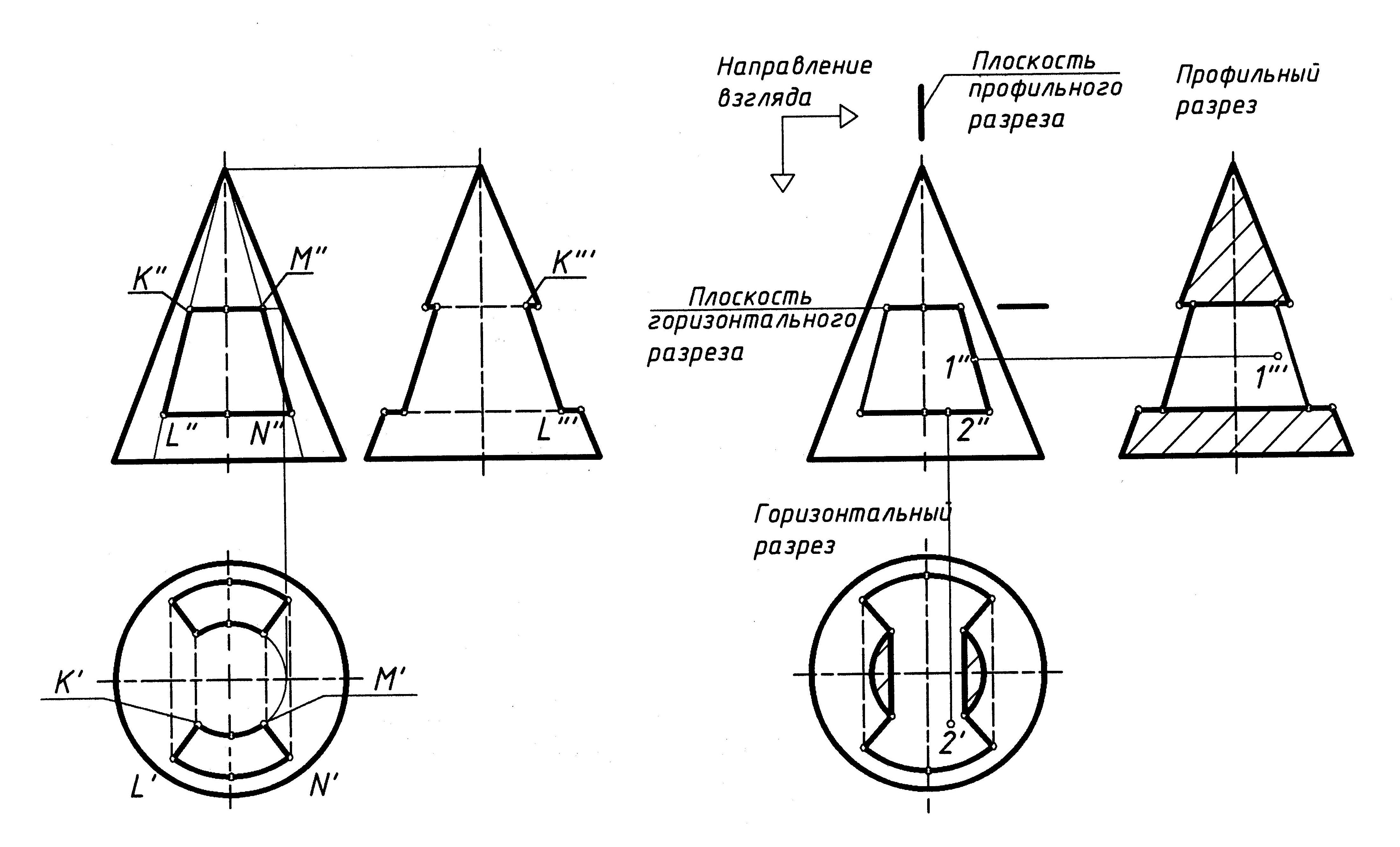
а б

Рис. 6

Сквозное отверстие ограничено по высоте двумя горизонтальными плоскостями, которые пересекают поверхность конуса по двум дугам окружностей между точками К и М и точками L и N. Обозначения присвоены только тем проекциям точек, которые видимы на проекциях фигуры. Две боковые плоскости отверстия проходят через вершину конуса и пересекают его поверхность по образующим. Часть образующих конуса вырезана сквозным отверстием, поэтому очерк конуса на профильной плоскости проекций приобретает вид ломаной линии.

Для выявления невидимых внутренних поверхностей на рис. 6, б построены два разреза: горизонтальной и вертикальной (профильной) плоскостями (положение плоскостей разрезов и направление взгляда указаны на чертеже). При этом на горизонтальном разрезе открывается нижняя горизонтальная плоскость отверстия. Точка 2 (2',2") лежит на этой плоскости. На профильном разрезе стала видимой правая боковая плоскость отверстия. Точка 1 (1'',1'") принадлежит этой плоскости. Оба разреза сделаны независимо друг от друга как для целого конуса.

Сфера

На рис. 7 показано построение проекций сферы, усеченной фронтально-проецирующей плоскостью γ, наклоненной к горизонту под углом α°.

Рис. 7

Плоскость γ рассекает сферу по окружности диаметра d, которая на дополнительную плоскость проекций, параллельную плоскости γ проецируется в натуральную величину.

Фронтальная проекция этой окружности – отрезок прямой, совпадающий с фронтальной проекцией плоскости γ и заключенный между точками пересечения прямой с главным меридианом. Центр окружности – точка О (О', О", О''') – находится в середине отрезка и на пересечении плоскости γ с перпендикуляром, проведенном из центра сферы к плоскости γ.

Горизонтальная проекция окружности – эллипс. Центр эллипса точка О' является горизонтальной проекцией центра окружности диаметра d. Большую ось эллипса находят через горизонтальную проекцию параллели сферы, проходящей через точку О". Вместе с тем большая ось эллипса равна диаметру d окружности, по которой плоскость γ рассекла сферу.

Величина малой оси эллипса зависит от угла α наклона секущей плоскости γ к горизонту, ее определяют по чертежу. Аналогично строят эллипс, который является профильной проекцией окружности сечения.

На рис. 8 шар пересекает сквозное отверстие прямоугольной формы, четыре плоскости которого перпендикулярны фронтальной плоскости проекций.

Каждая из четырех плоскостей прямоугольного отверстия пересекает сферу по окружностям, которые проецируются либо в отрезки прямых линий, либо в дуги окружностей.

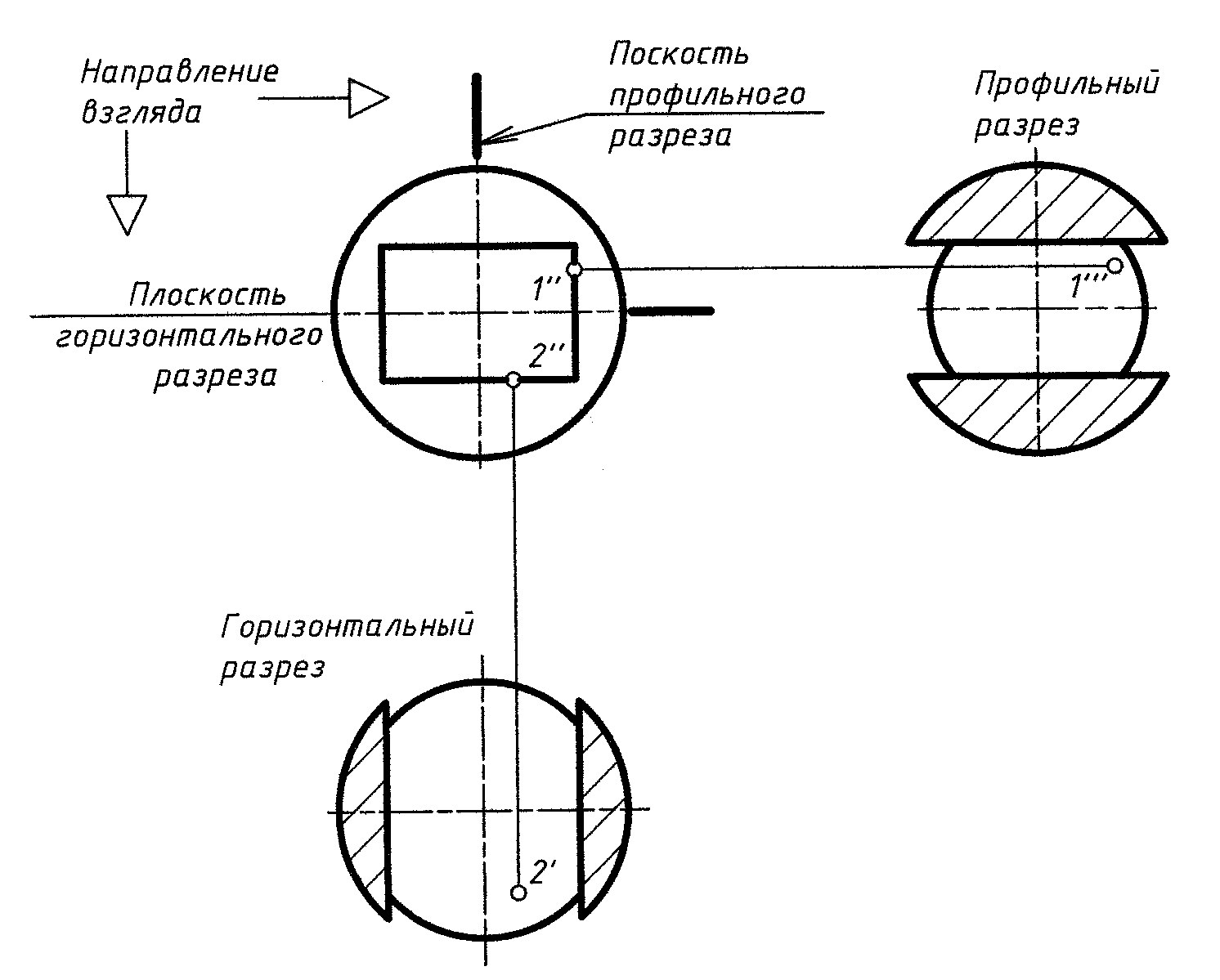
Рис. 8

Для того чтобы увидеть скрытые от наблюдателя внутренние поверхности предмета, изображенного на рис. 8 построены горизонтальный и профильный разрезы. Положение плоскостей разрезов и направление взгляда указаны. На горизонтальном разрезе становится видимой нижняя горизонтальная плоскость сквозного отверстия. Точка 2 (2', 2") принадлежит этой плоскости. На профильном разрезе «открывается» правая плоскость прямоугольного отверстия. Точка 1(1', 1") лежит на этой плоскости. Оба разреза сделаны независимо друг от друга как для целого шара.

Лекция №6 (ИУ1, 2, 4);№7(ИУ3, 8, 5, 6)