1. Кривые линии

Линии делятся на плоские и пространственные.

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими; если точки кривой не принадлежат одной плоскости, кривые называются пространственными.

Чтобы задать проекции кривой линии, надо задать проекции ряда ее точек. При этом обязательно задают проекции характерных точек кривой (рис. 1).

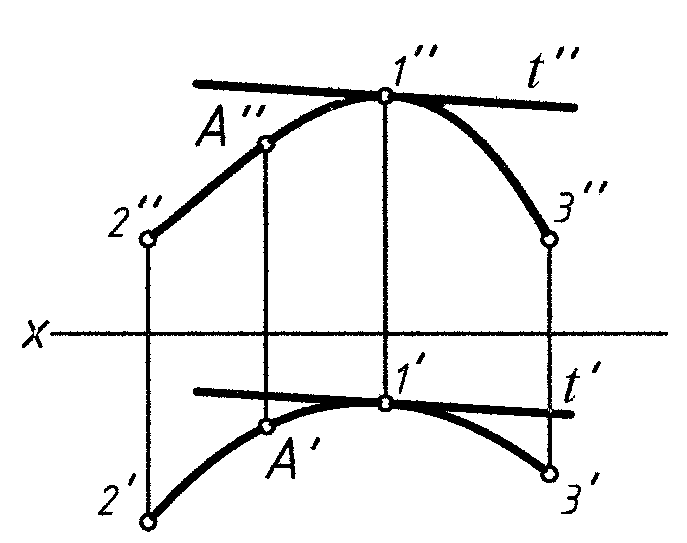
Рис. 1

1 – 2 – 3 – характерные точки

А – промежуточная точка

t – касательная – предельное положение секущей. Касательная к кривой проецируется, в общем случае, в касательную к проекции кривой в заданной точке.

Проекции окружности

Окружность может проецироваться в окружность, прямую и в эллипс (рис. 2).

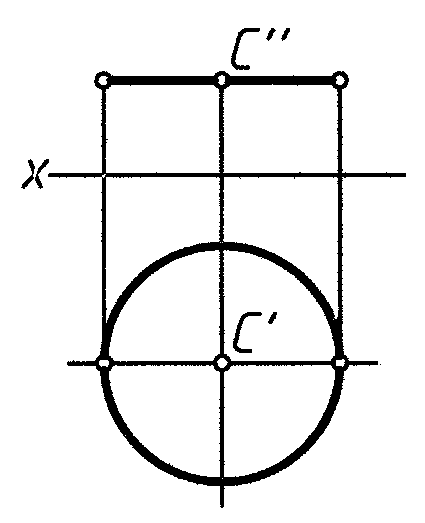
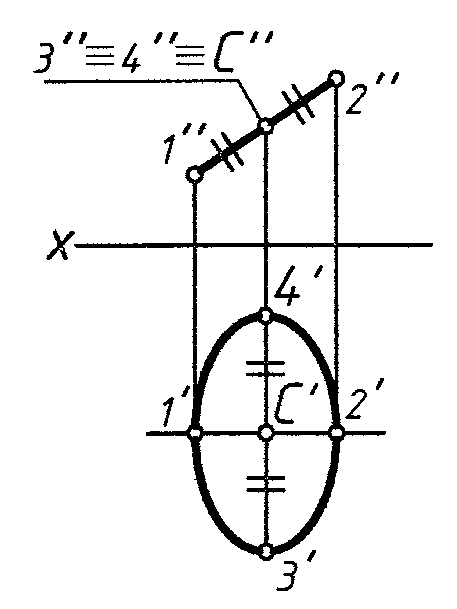
Рис. 2

Построение эллипса по двум осям (р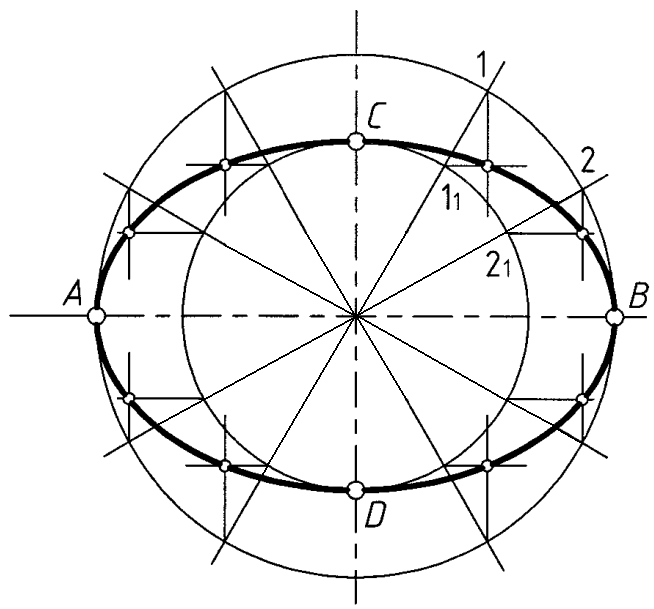ис. 3)

Рис. 3

2. Образование и задание поверхностей

Все поверхности можно изобразить на плоскости, задавая проекции линий и точек, принадлежащих поверхности.

В общем случае, для любой поверхности изображение может быть выполнено двумя семействами линий: направляющими и образующими. Для сложных поверхностей задают каркас поверхности. Линии каркаса обычно получаются при сечении поверхности плоскостями (α_i и β_i), расположенными под углом 90⁰ и параллельными плоскостям проекций (рис. 4).

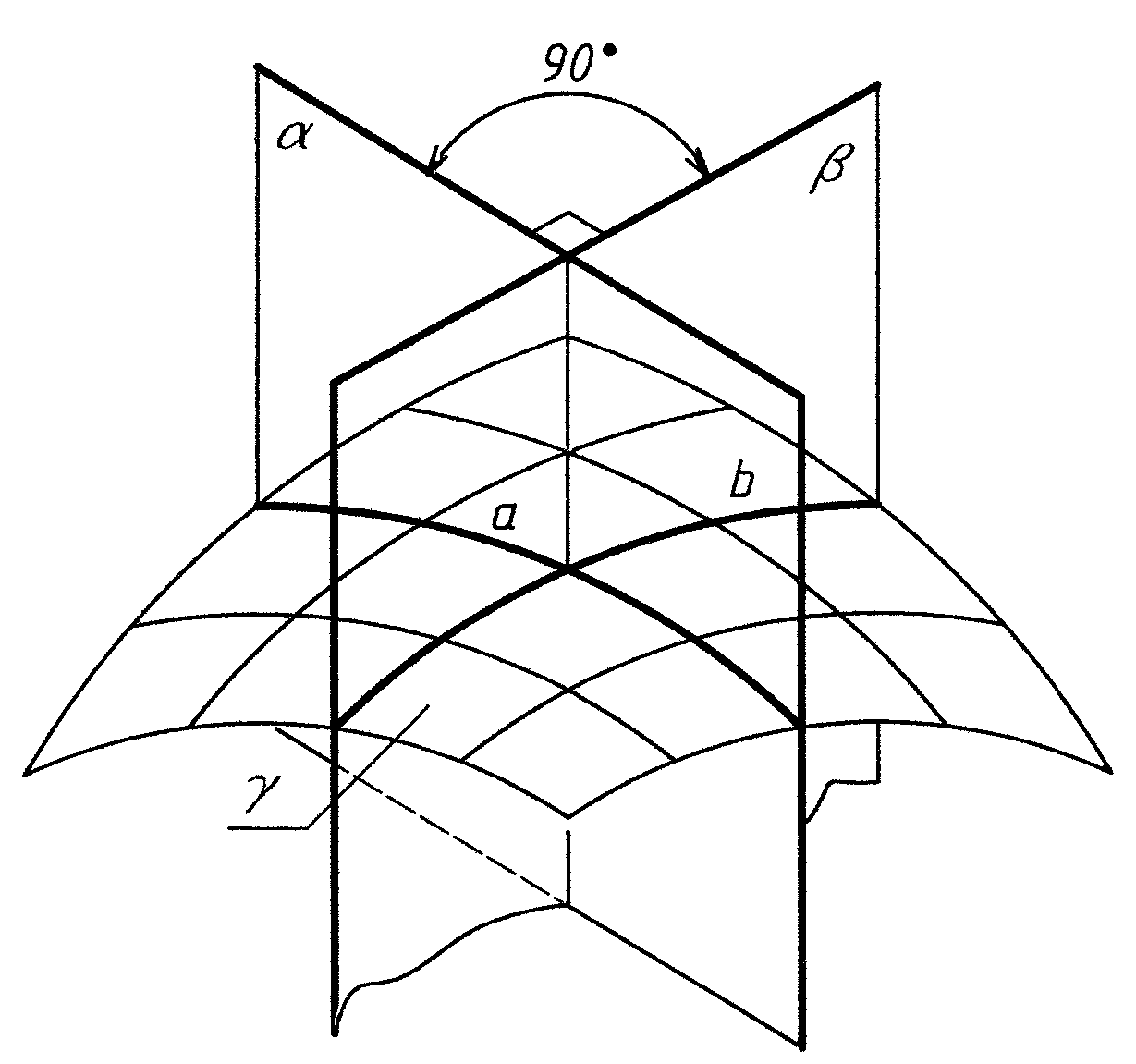
Рис. 4

Для поверхностей можно задавать также проекции направляющей d и указывать, как строится образующая g, проходящая через любую точку направляющей. Направляющие и образующие могут меняться местами.

Н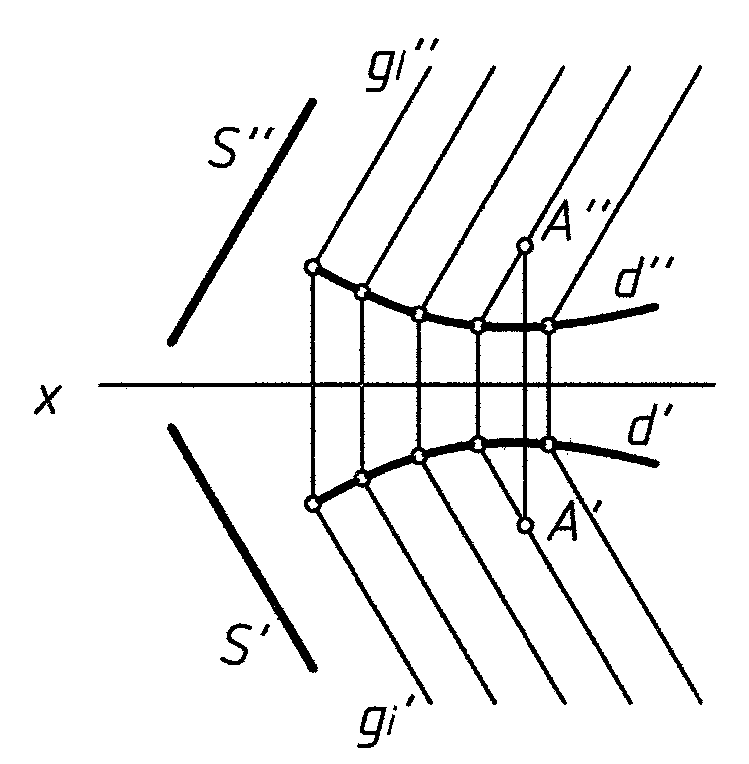 а рис. 5 задана цилиндрическая поверхность.

Рис. 5

S – линия, определяющая направление образующих g_i,

g_i ∩ d; g_i // S

Поверхность считается заданной на чертеже, если можно построить проекцию любой точки, ей принадлежащей.

Точка A принадлежит поверхности (см. рис. 5), если она принадлежит линии, принадлежащей поверхности.

Для большей наглядности в ряде случаев используют очерк поверхности.

О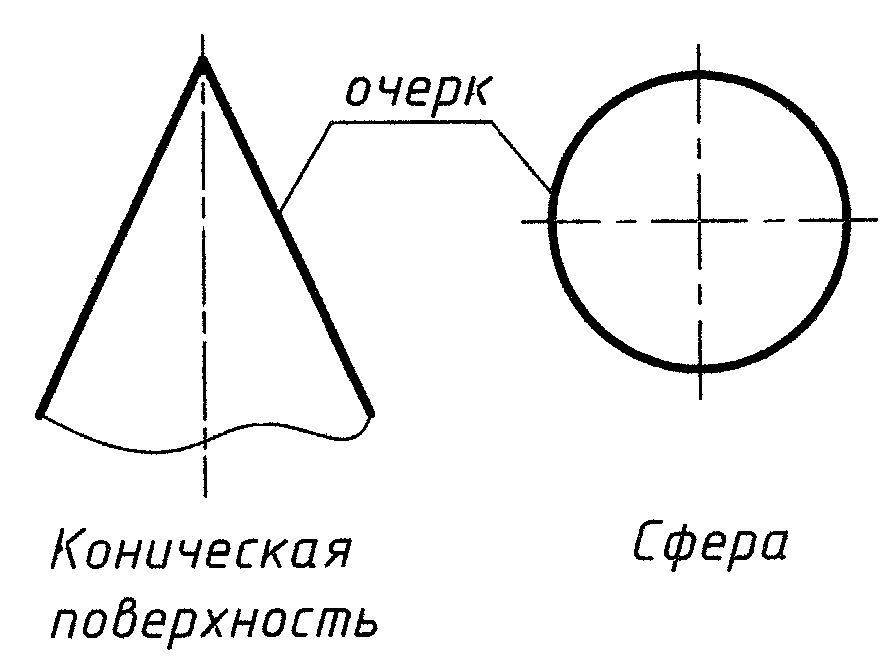 черком поверхности называются линии, которые ограничивают область ее проекций (рис.6).

Рис. 6

Обзор поверхностей

Большое разнообразие поверхностей. Не удается классифицировать поверхности по какому-либо одному важнейшему признаку.

Можно группировать поверхности:

1) с позиций геометрической характеристики:

- по форме образующей: линейчатые, нелинейчатые;

- по движению образующей: вращение, винтовое, параллельный перенос;

2) с позиций технологии изготовления:

-по возможности развернуть на плоскость: развертываемые, неразвертываемые.

Одна и та же поверхность может быть образована разными образующими с разными движениями их.

Н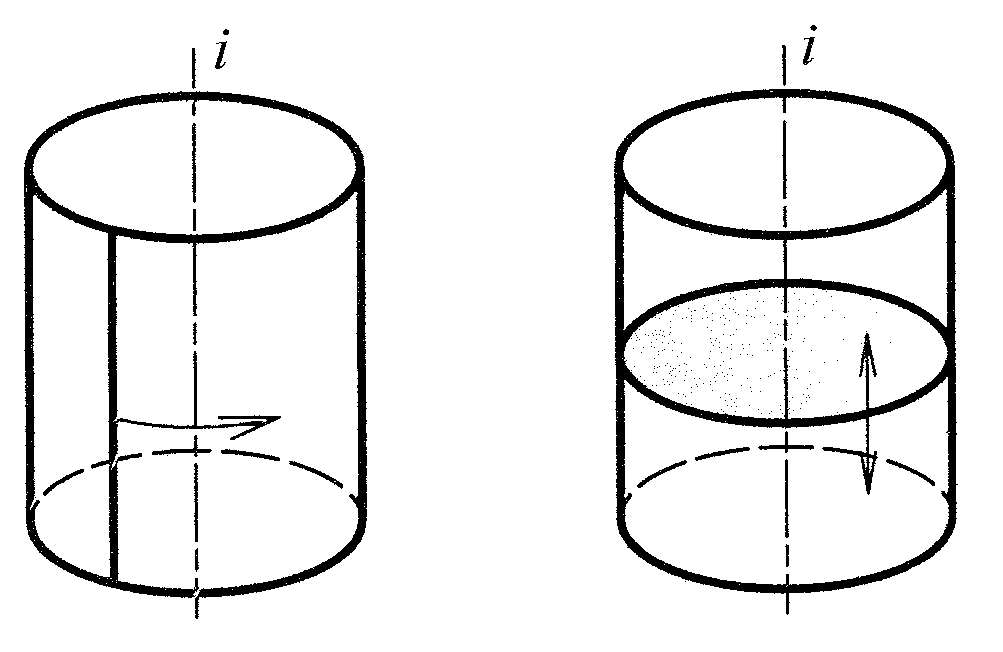 а рис. 7 показана цилиндрическая линейчатая развертываемая поверхность (может быть представлена поверхностью вращения и может быть представлена поверхностью параллельного переноса).

Рис. 7