2. Проекции многогранников

Многогранник – часть пространства (тело), ограниченная отсеками пересекающихся плоскостей. Отсеки плоскостей (многоугольники) – грани, линии их пересечения – ребра. Ребра пересекаются в точках – вершинах многогранника.

Построение проекции многогранника сводится к построению его ребер и вершин.

Рассмотрим проекции призмы и пирамиды. На рис. 22 заданы проекции прямой правильной треугольной призмы. На рис. 23 заданы проекции прямой правильной шестиугольной пирамиды.

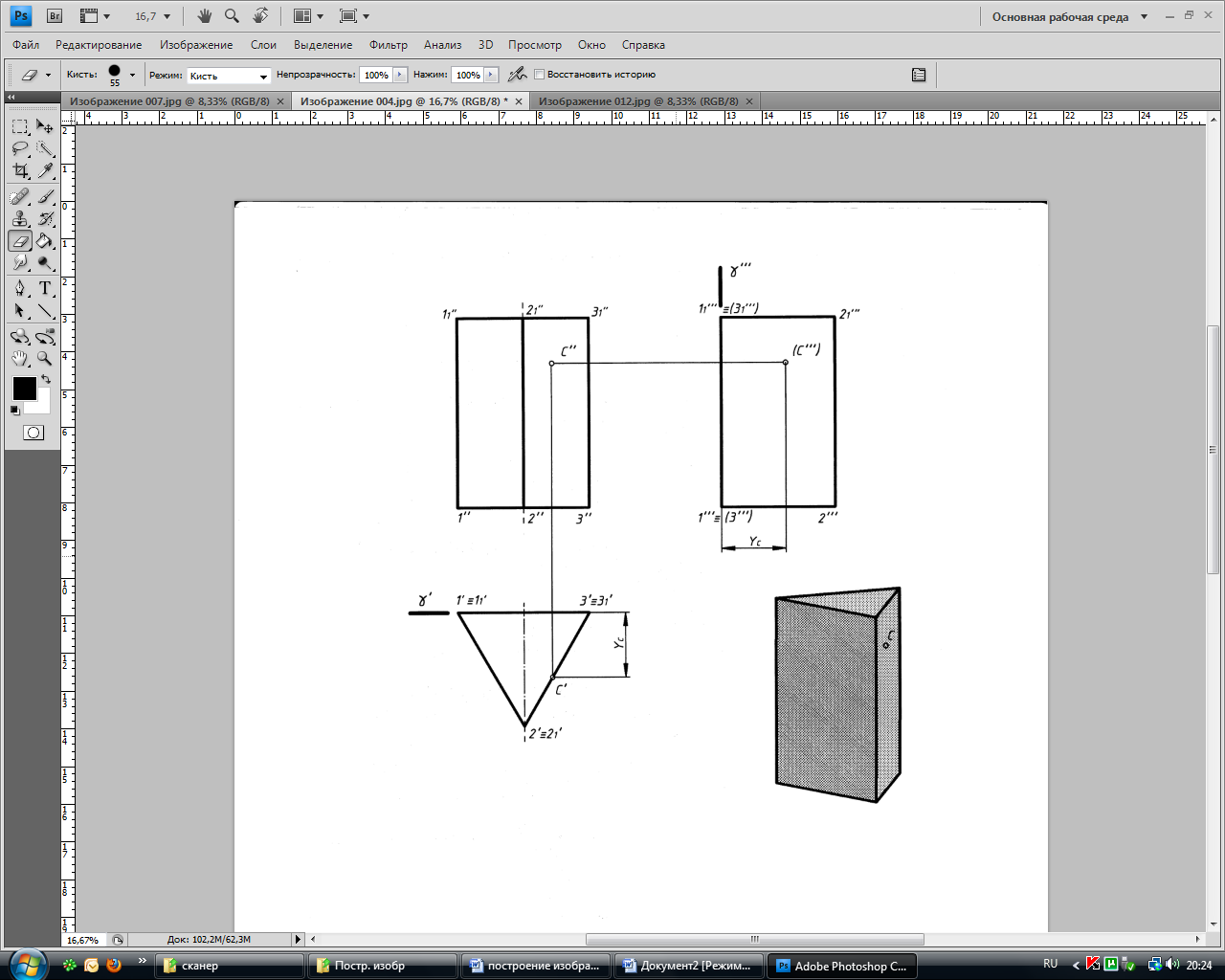
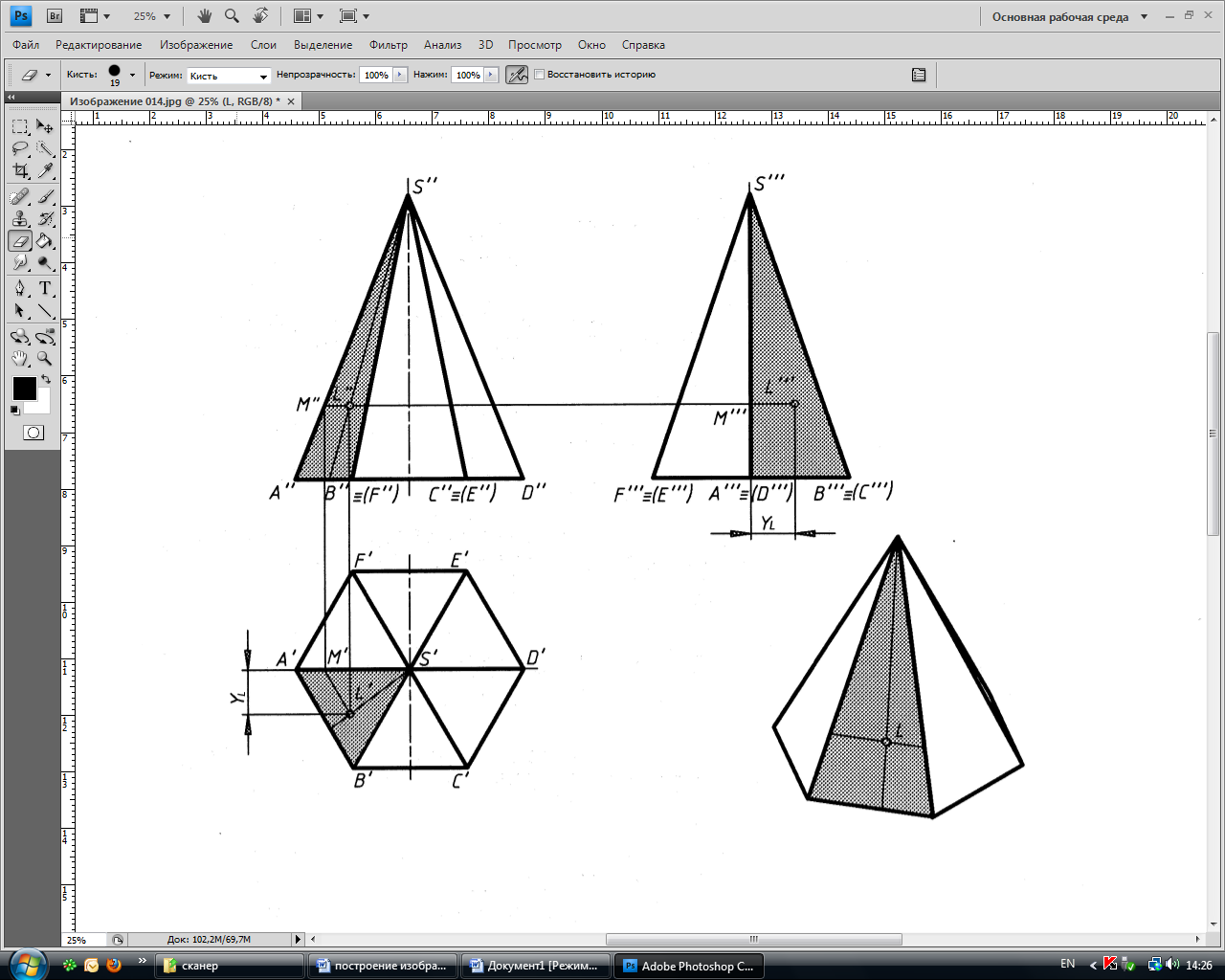
Рис. 22 Рис. 23

Признаки изображения призмы:

- наличие на чертеже только прямолинейных отрезков, которые являются проекциями ребер или граней;

- наличие параллелограммов или прямоугольников как проекций боковых граней;

- наличие любого многоугольника как проекции основания.

Для задания пирамиды на чертеже надо иметь фигуру сечения всех боковых граней пирамиды плоскостью (основание) и точку пересечения ребер боковых граней (вершина).

Во всех случаях целесообразно располагать основание призмы и пирамиды параллельно плоскости проекций.

Лекция№3 (ИУ для всех)

1. Способы преобразования

Частные положения фигур относительно плоскостей проекций более удобны для решения геометрических задач в первую очередь метрических задач (определение длины, угла, площади).

Можно отметить два пути решения задачи изменения положения фигуры относительно плоскостей проекций:

1. изменить положение плоскостей проекций, не изменяя положения фигуры;

2. изменить положение фигуры, не меняя положения плоскостей проекций.

Способ замены плоскостей проекций

Условия преобразования:

1. положение фигуры неизменно;

2. изменяется положение одной из двух плоскостей проекций;

3. новую плоскость проекций располагают перпендикулярно оставшейся плоскости проекций (рис 1).

Рис. 1

4. Положение новой плоскости проекций может быть задано или выбрано.

Построение профильной проекции точки (фигуры) есть также использование способа замены плоскостей проекций (рис. 2)

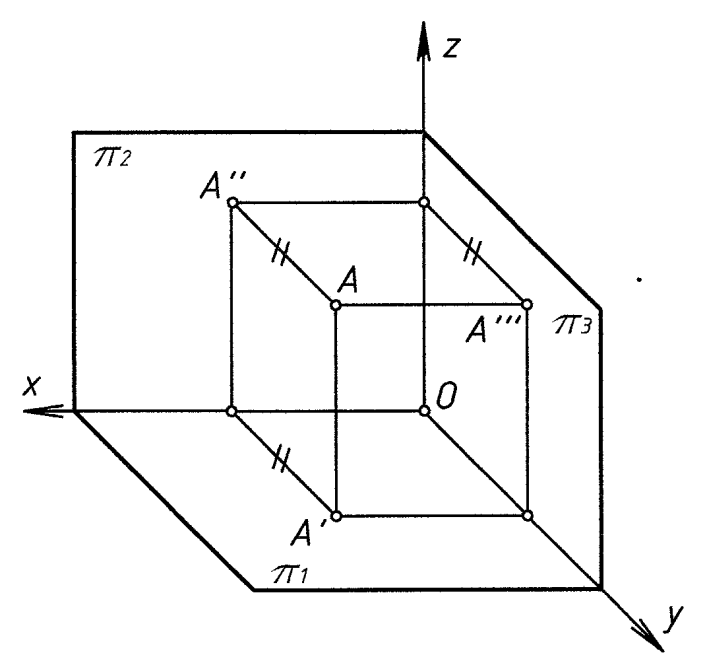
Рис. 2

Метрические задачи, решаемые способом замены плоскостей проекций:

Примеры задач.

Задача 1. Определить длину отрезка (рис. 3)

Задача 2. Преобразовать прямую общего положения в проецирующую (см. рис. 37)

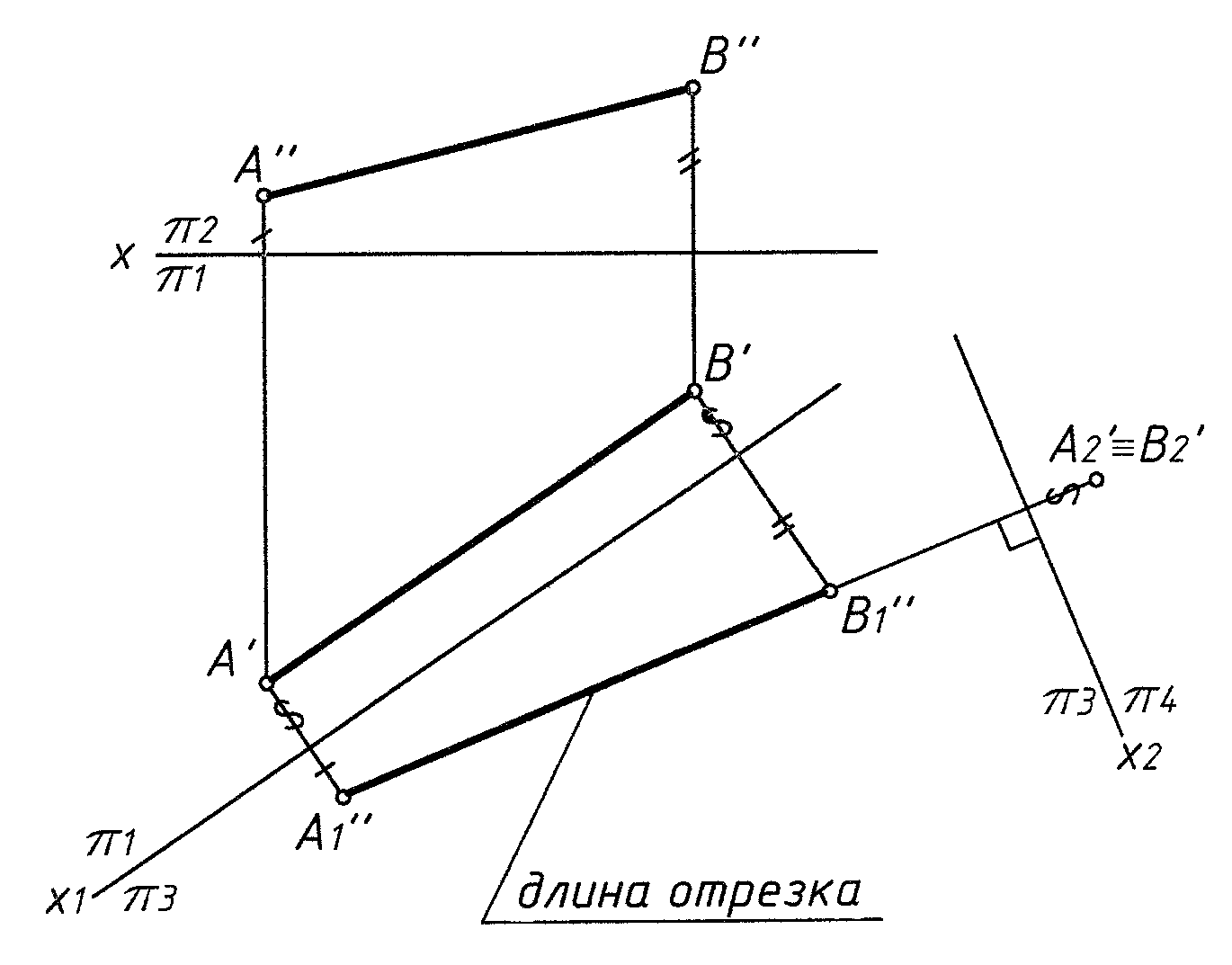
Первая замена

z = const

Вторая замена

y = const

Рис. 3

Задача 3. Преобразовать плоскость общего положения в проецирующую.

Определить угол наклона плоскости к горизонтальной плоскости проекций (рис. 4).

Задача 4. . Преобразовать плоскость общего положения в плоскость уровня (см. рис. 38).

О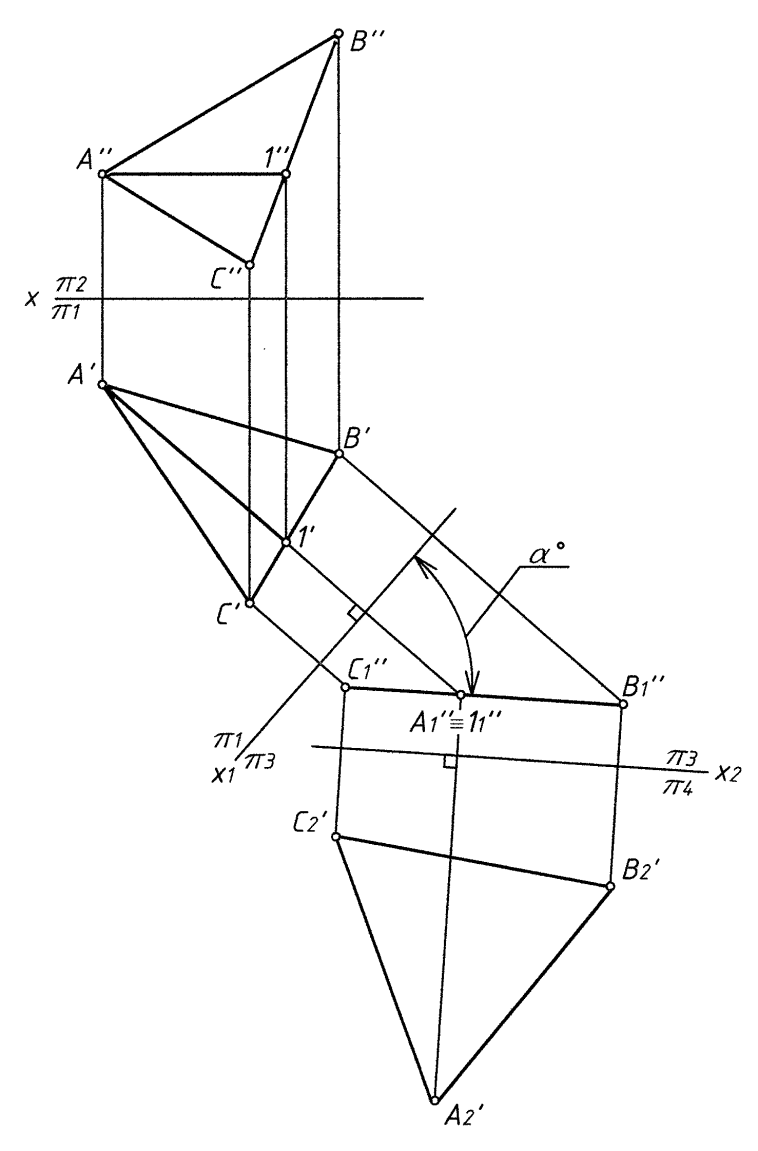 пределить истинный вид плоскости ∆ ABC.

Рис. 4

Способ вращения вокруг проецирующей прямой – частный случай плоско-параллельного перемещения.

Условия преобразования:

1. ось вращения i неподвижна и перпендикулярна плоскости проекций;

2. все точки фигуры перемещаются по окружностям, плоскости которых перпендикулярны оси i (рис.5);

3. точки лежащие на оси вращения i неподвижны (см. рис. 5)

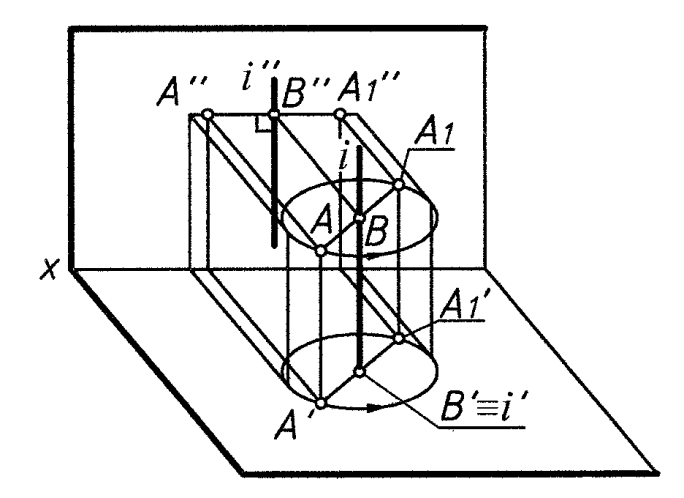
Рис. 5

Пример задачи:

О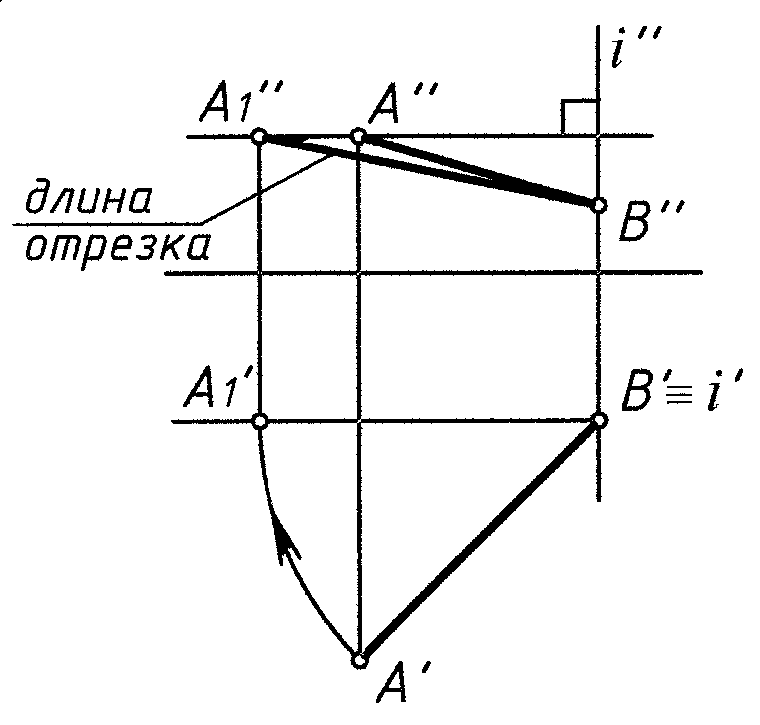 пределить длину отрезка вращением вокруг проецирующей прямой (рис. 6)

Рис. 6