Построение проекций точек и прямых, принадлежащих плоскости

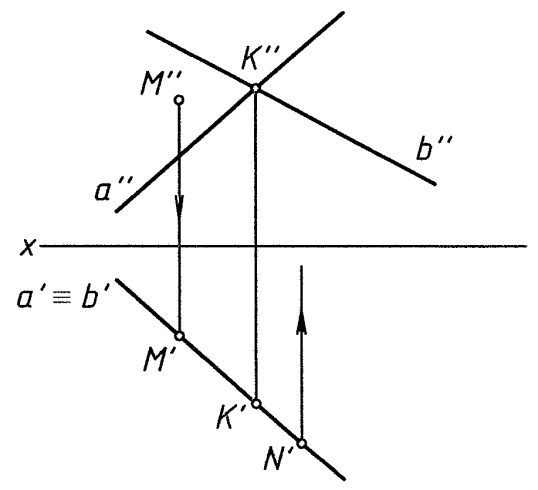
M′′ – задана

M′ принадлежит а′ ≡ b′

N′ – задана. Тогда – множество решений

(Надо доп. условия)

Рис. 4

В общем случае для построения проекции точки, принадлежащей плоскости общего положения, надо воспользоваться проекциями прямой, принадлежащей заданной плоскости и проходящей через точку (используем свойство принадлежности).

Линии частного положения в плоскости

Г оризонталь h плоскости принадлежит плоскости и параллельна плоскости π₁ (рис. 5)

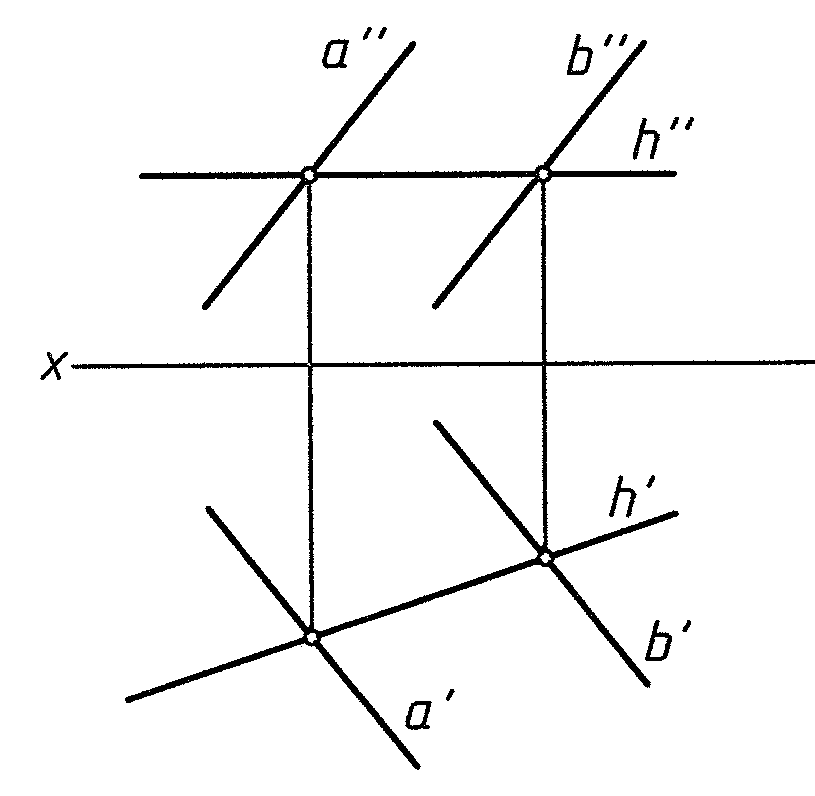
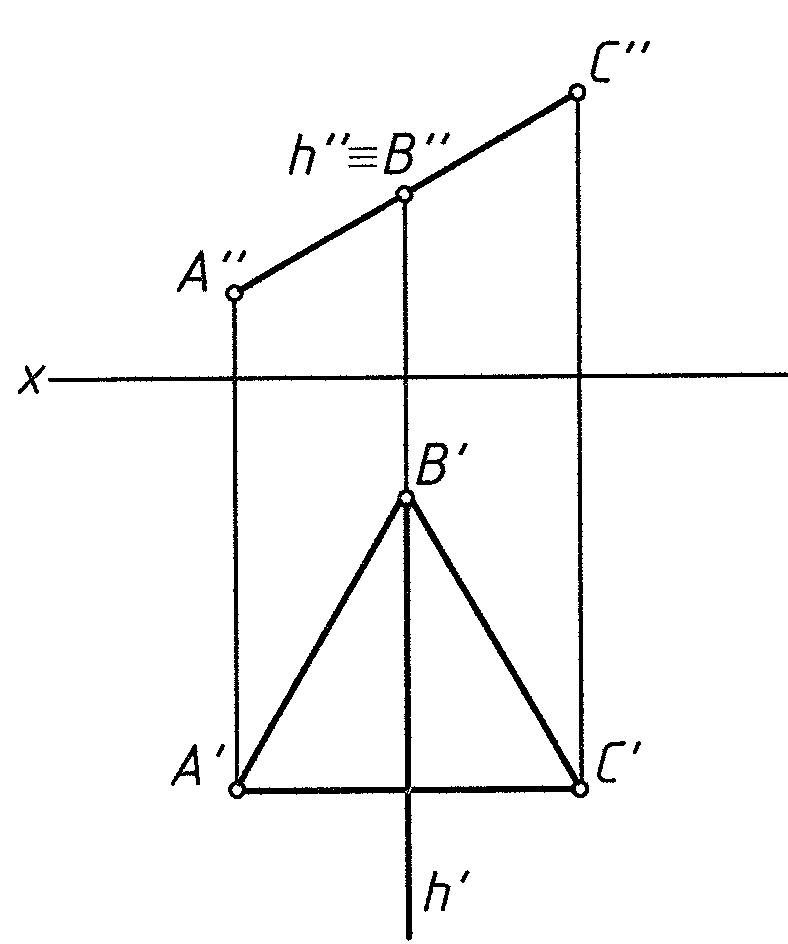
Пл. (a || b) общего положения Пл. ∆ ABC _┴ π₁ Пл. ∆ ABC _┴ π₂,

в этом случае h _┴ π₂

Рис. 5

Ф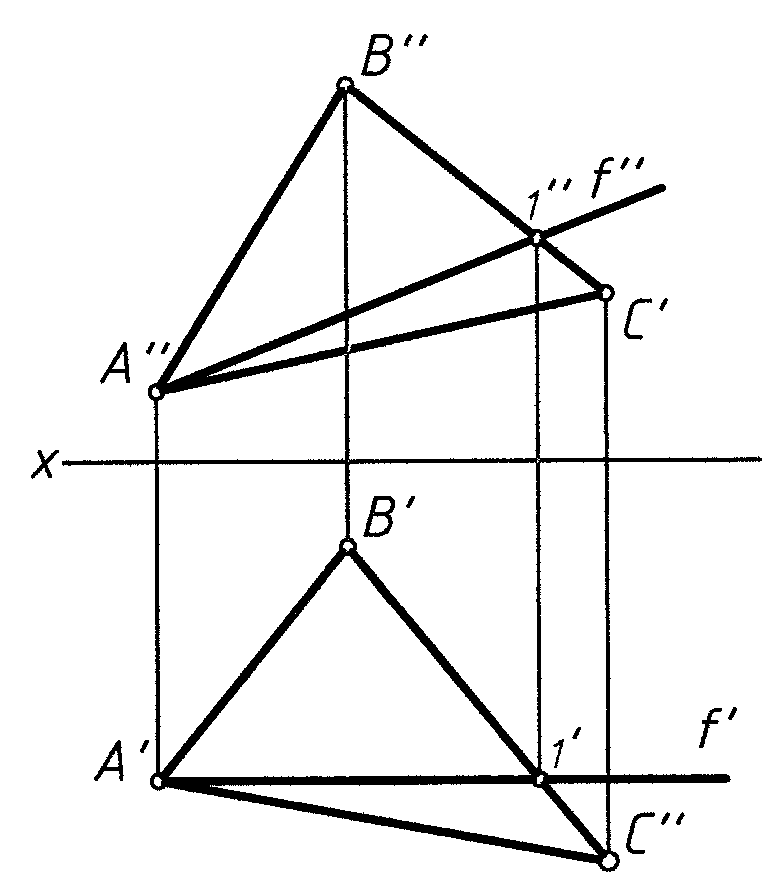 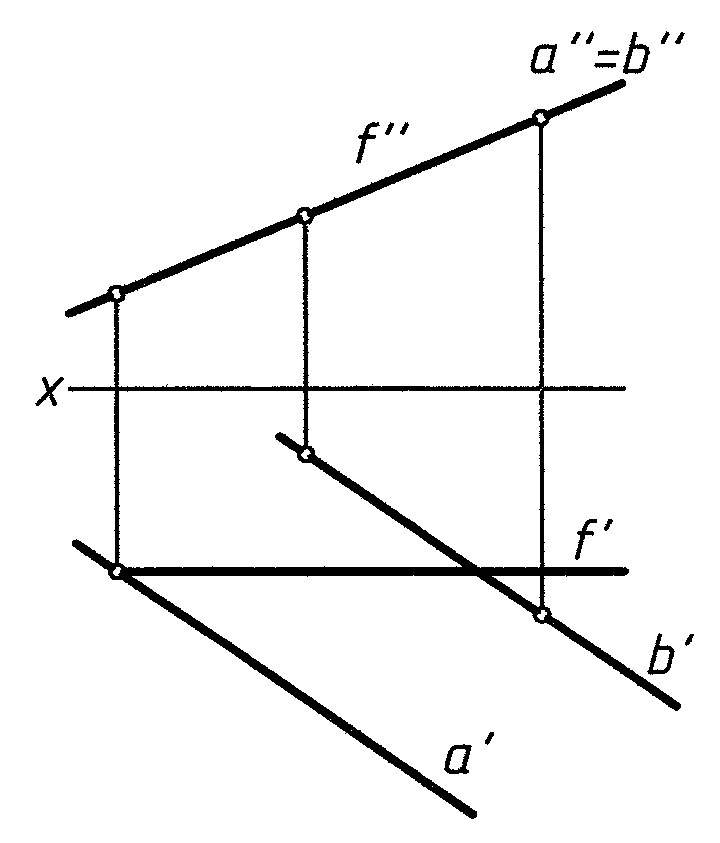ронталь f плоскости принадлежит плоскости и параллельна плоскости π₂ (рис. 6)

Пл. ∆ ABC – общ. положения Пл. ∆ ABC _┴ π₁, Пл. ∆ ABC _┴ π₂

в этом случае f _┴ π₁

Рис. 6

Взаимное положение двух прямых (рис. 7)

Параллельны. Пересекаются. Скрещиваются.

l || m l ∩ m l ∙ m

конкурирующие точки 1 и 2

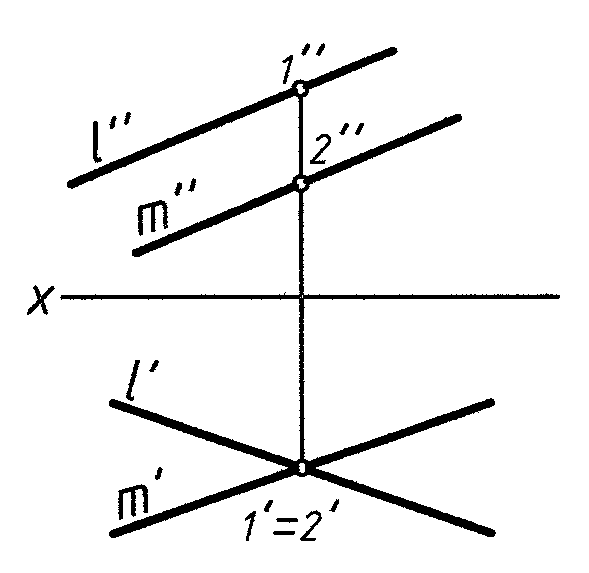
Рис. 7

Теорема о проецировании прямого угла (рис. 8). Если одна сторона прямого угла параллельна плоскости проекций, а вторая сторона не перпендикулярна к ней, то прямой угол проецируется без искажения на данную плоскость проекций.

Дано: m ∩ l; m _┴ l; l // π₁

При проецировании l′ _┴ m′

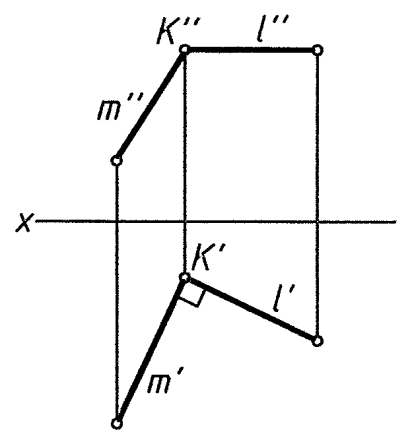
Рис. 8

Отметим, что угол между скрещивающимися прямыми равен углу между параллельными им пересекающимися прямыми.

Параллельность и перпендикулярность прямой и плоскости

Построение на чертеже параллельных прямой и плоскости основано на использовании признака параллельности прямой и плоскости и свойства прямоугольного проецирования о проекции параллельных прямых (рис. 9)

Задача

В плоскости построить прямую, параллельную заданной прямой

Задача

Через заданную точку K построить плоскость, параллельную заданной прямой m и перпендикулярную плоскости π₁

m || n

m || b

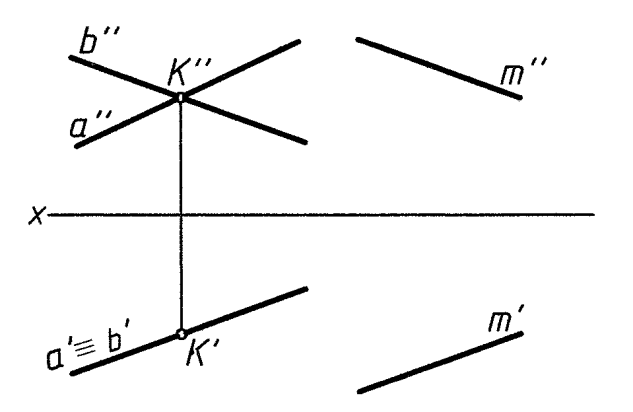
Рис. 9

Построение на чертеже перпендикулярных прямой и плоскости основано на использовании признака перпендикулярности прямой и плоскости и теоремы о проецировании прямого угла (используем горизонталь и фронталь) (рис. 10).

n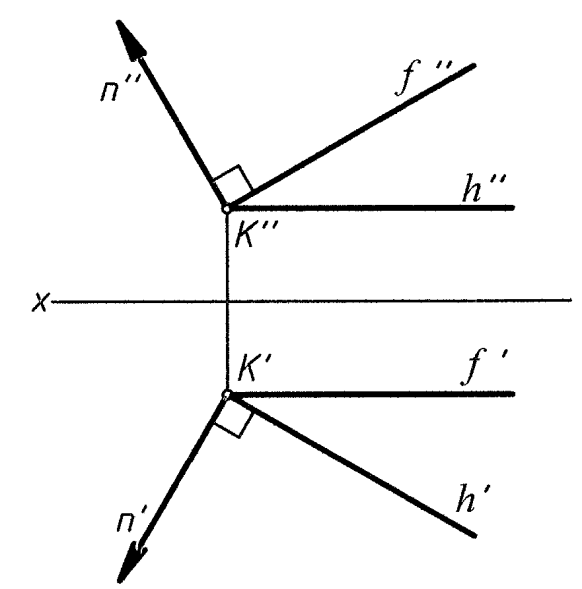 (n′ n″) – нормаль плоскости

Рис. 10

Параллельность и перпендикулярность двух плоскостей

Построение на чертеже параллельных плоскостей основано на использовании признака параллельности двух плоскостей и свойства прямоугольного проецирования о проекции параллельных прямых (рис. 11)

a || AB Плоскости параллельны и

b || AC перпендикулярны плоскости π₂

Рис. 11

Построение на чертеже перпендикулярных плоскостей основано на использовании признака перпендикулярности двух плоскостей и теоремы о проецировании прямого угла (в этом случае следует использовать горизонталь и фронталь).

Рассмотрим пример (рис. 12). Через прямую a провести плоскость, перпендикулярную к плоскости треугольника ABC.

A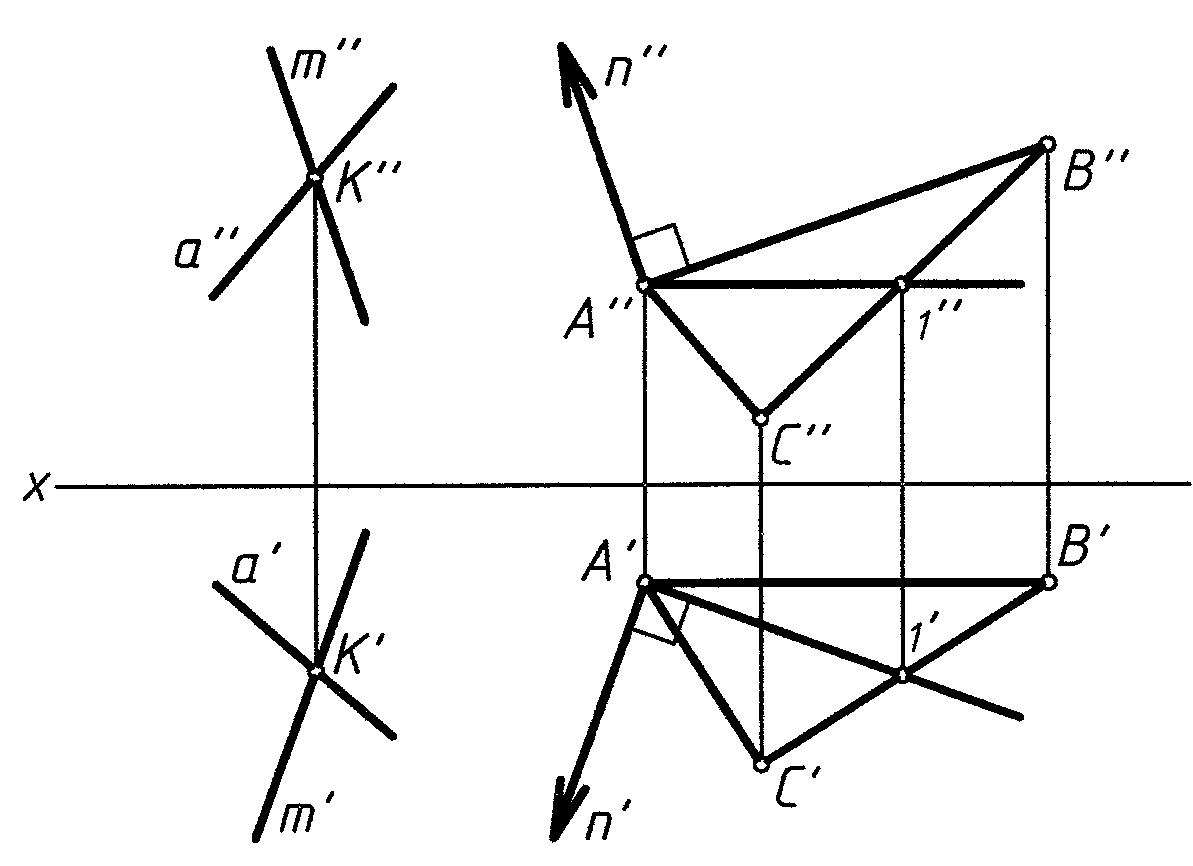 1 – горизонталь; AB – фронталь

n _┴ ∆ABC, т.к. n′ _┴ A′1′; n″ _┴ A″B″;

m″// n″; m′// n′;

m _┴ ∆ABC;

Рис. 12