11. Развертки поверхностей
Разверткой поверхности называется фигура, полученная в результате совмещения поверхности с плоскостью, при отсутствии разрывов и складок на развертке.
Развертываемых поверхностей три: цилиндрическая, коническая, с ребром возврата (рис. 1,2).
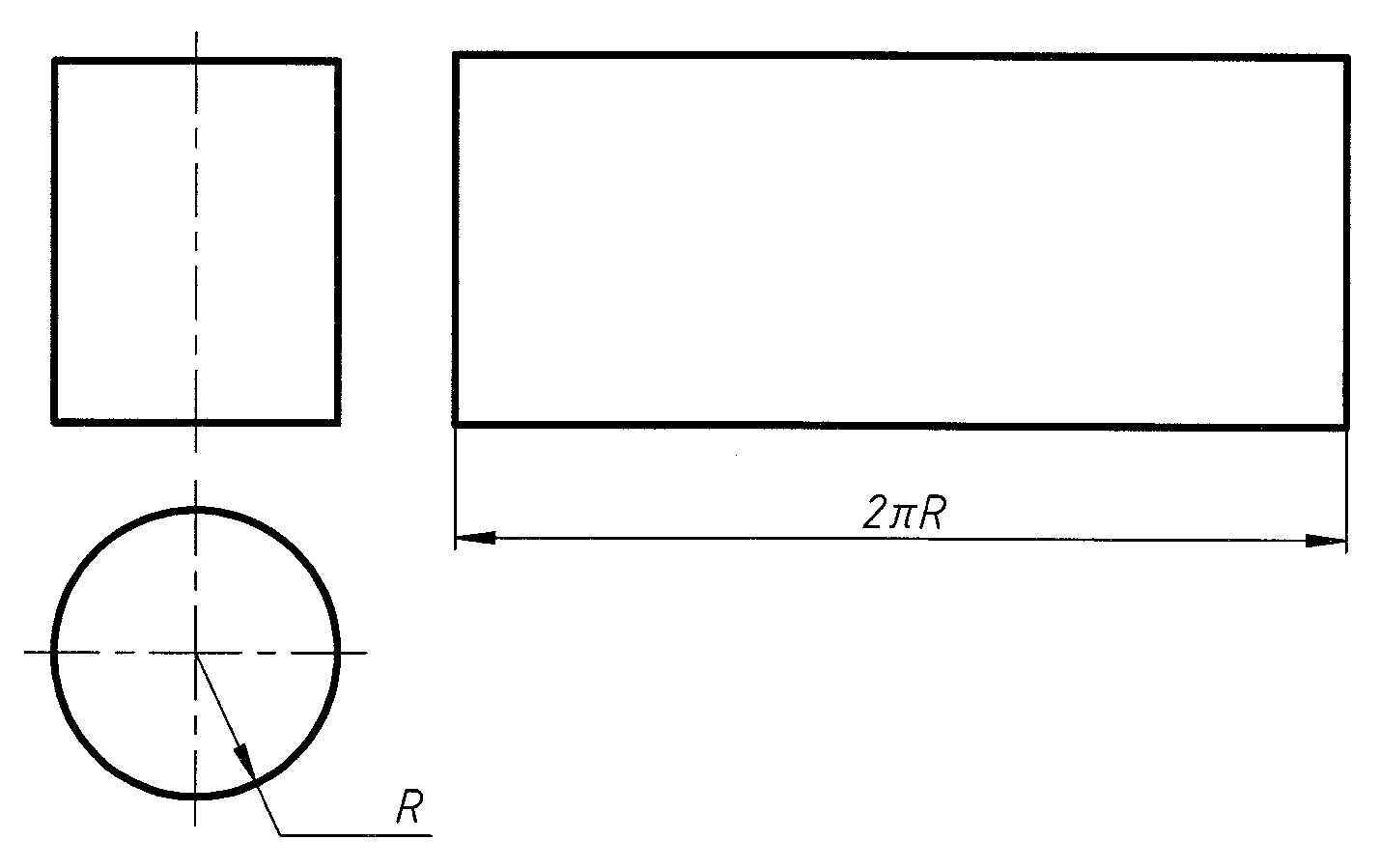
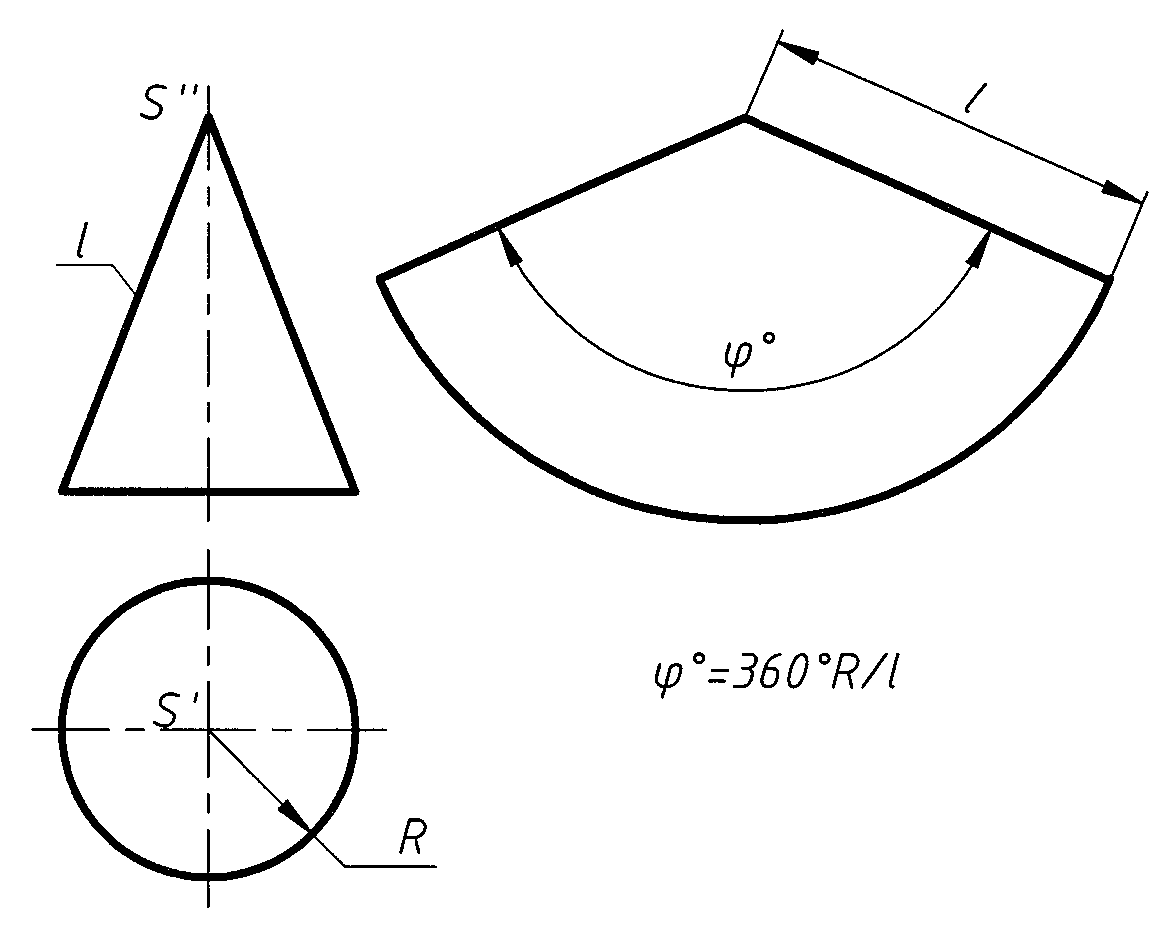
Рис. 1 Рис. 2
Практически развертки этих поверхностей получают, заменяя поверхности гранными фигурами: для цилиндрической поверхности делают развертку вписанной (или описанной) в поверхность призмы; для конической - пирамиды (рис. 2). При этом получаю приближенные развертки с необходимой точностью, увеличивая число граней призмы или пирамиды.
Рис. 2
Гранные поверхности развертывают, разрезая по некоторым ребрам и совмещая грани с плоскостью. При этом определяют истинную величину ребер и граней фигуры.
Неразвертываемых поверхностей большинство.
Можно аппроксимировать (приближенно заменить) заданную поверхность гранной поверхностью с любой точностью. В общем случае поверхность аппроксимируют многогранной поверхностью, состоящей из треугольников (способ триангуляции) (рис. 3).
Рис. 3
Можно заменить неразвертываемую поверхность набором развертываемых поверхностей и получить условную развертку заданной поверхности (рис. 4).
Рис. 4