Прямоугольные аксонометрические проекции
В прямоугольной аксонометрии коэффициенты искажения связаны зависимостью
k2x + k2y + k2z = 2.
Изометрическая проекция. Так как kx = ky = kz, то 3k2 = 2; k =2/3 = 0,82
Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям x α, y α, z α, т.е. приняв коэффициенты искажения равным 1, что соответствует увеличению линейных размеров изображения по сравнению с действительными в 1/0,82 = 1,22 раза.
Диметрическая проекция. Если взять k = kx = kz и ky = ½ kx, то получим, 2k2 + k2/4 = 2; k2 = 8/9; k = 8/9 = 0,94; kx = kz = 0,94; ky = 0,47
Диметрическую проекцию, как правило, выполняют без искажения по осям x α, z α и с коэффициентом искажения 0,5 по оси y α. В этом случае линейные размеры увеличиваются на аксонометрической проекции в 1/0,94 = 1,06 раза.
Углы между аксонометрическими осями См. Гост
Изометрия Диметрия
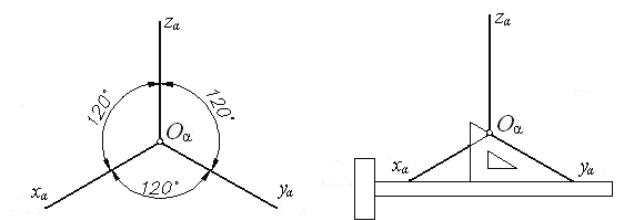
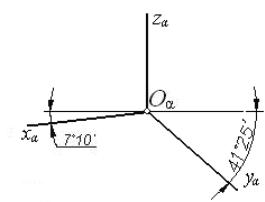
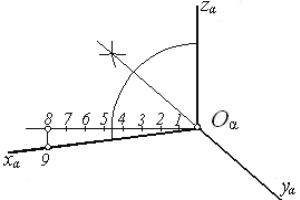
Рис. 2 Рис. 3
Построение аксонометрической проекции окружности
При построении аксонометрических проекций часто приходится строить изображения окружностей, расположенных в координатных плоскостях xy, xz, yz или в плоскостях, им параллельным. В этом случае нормалями к плоскостям окружностей являются соответственно оси x, y, z. Следовательно, направление больших осей эллипсов, изображающих проекции окружностей, всегда перпендикулярны соответственно осям x α, y α, z α (рис. 4, 5), а малые оси совпадают по направлению с этими осями. Большие оси соответствуют тем диаметрам изображаемых окружностей, которые параллельны картинной плоскости.
Изометрия Диметрия
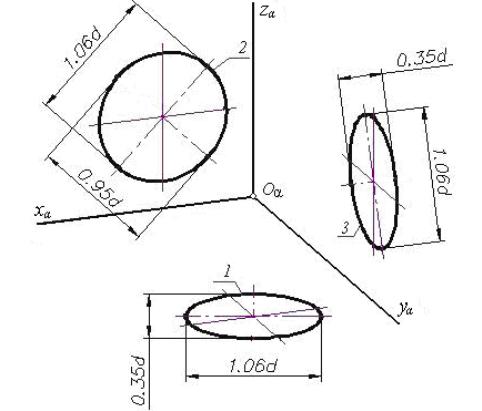
Рис. 4 Рис. 5
Условности при выполнении аксонометрических проекций
Согласно ГОСТ 2.317-2011 «Аксонометрические проекции» линии штриховки сечений в аксонометрических проекциях наносятся параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.
На рис. 6 показано построение направлений линий штриховки в изометрии. Для этого на осях xα, yα, zα (или линиях, им параллельным) откладывают равные отрезки произвольной длины и соединяют их концы.
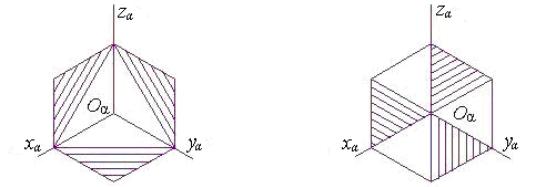
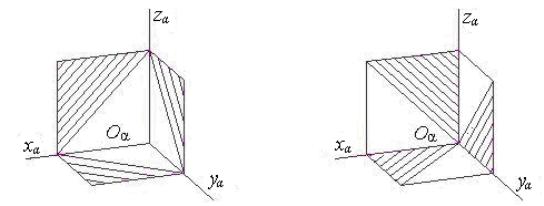
Рис. 6 Рис. 7
На рис. 7 показано построение направлений линий штриховки в диметрии. Для этого на осях xα и zα (или линиях им параллельным) откладывают равные отрезки произвольной длины, а на оси yα (или линии ей параллельной) – отрезок вдвое меньший и соединяют их концы.
Пример построения аксонометрической проекции
Пример построения аксонометрической проекции фигуры приведен на рис. 8. Построение начинаем с вычерчивания фигур сечений, расположенных в плоскостях выреза.
Рис. 8
Прямоугольная изометрия более распространена как более простая в построении.