Лекции по начертательной геометрии
Лекция №1(ИУ1,2,4,3,8,5,6)
Введение
Предметом начертательной геометрии является изложение и обоснование правил построения изображений пространственных форм на плоскости и решение геометрических задач по заданным изображениям этих форм.
Предметы (пространственные формы) в Евклидовом пространстве имеют три измерения. Изображения на плоскости – двумерные. На плоскости могут быть только линии. Пространственные формы ограниченны поверхностями. Поверхность – результат перемещения линии в пространстве (линия – образующая поверхности). Перемещение линии также может быть заданно с помощью линий (линия – направляющая поверхности).
Линия – результат перемещения в пространстве точки или результат пересечения поверхностей.
Точка – элементарный геометрический объект. Точка – результат пересечения двух линий.
Пространство представляет собой множество точек.
1. Метод проекций
В основе правил построения изображений, рассматриваемых в начертательной геометрии и применяемых в инженерной практике, лежит метод проекций. Так как пространственные формы рассматриваются как множество, принадлежащих им точек, то все правила будем рассматривать на примере построения проекций точки.
Принятые обозначения:
В пространстве |
На плоскости |
точки |
|
A, B, C… |
A′; B′; C′; A′′; B′′; C′′… |
линии |
|
a , b , c , l… |
a′; b′; … a′′; b′′… |
поверхности |
|
α, β, γ… |
α′; β′; γ′… |
Условия получения изображений:
- каждому геометрическому элементу (предмету) – одно, только ему соответствующе изображение;
- каждому изображению соответствие одного предмета пространства с заданными геометрическими характеристиками (форма, размер, расположение).
Проекции с использованием прямых линий – проецирующих лучей
Центральные проекции Параллельные проекции
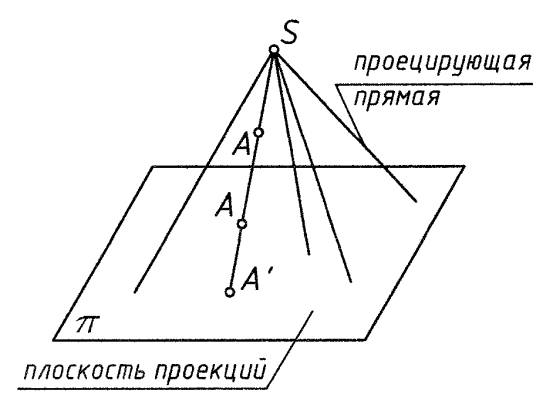
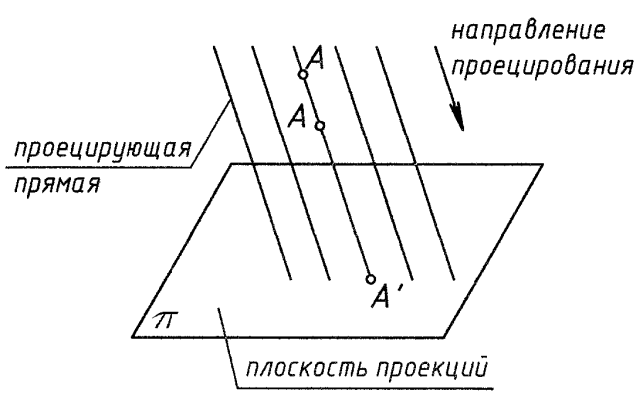
Рис. 1
Проекция точки (A') – точка пересечения проецирующей прямой, проходящей через заданную точку пространства (А) с плоскостью проекций (π).
Способ двух изображений
Только одна проекция точки не определяет ее положения в пространстве.
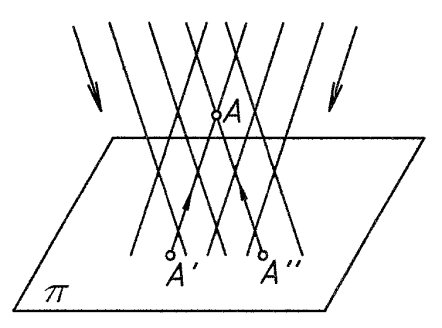
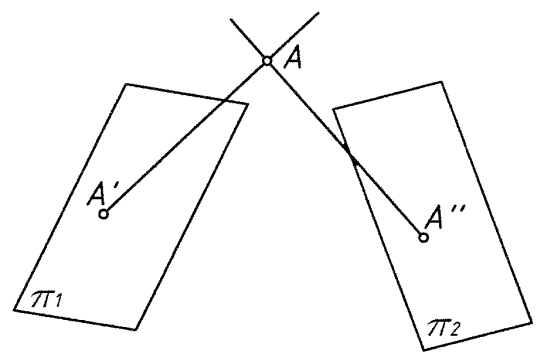
Рис. 2
Положение точки в пространстве можно определить, имея две ее проекции на плоскости. Любая поверхность может быть представлена как некоторое упорядоченное, двухпараметрическое множество точек.
Прямоугольные проекции
(лежат в основе выполнения чертежей в машиностроении)
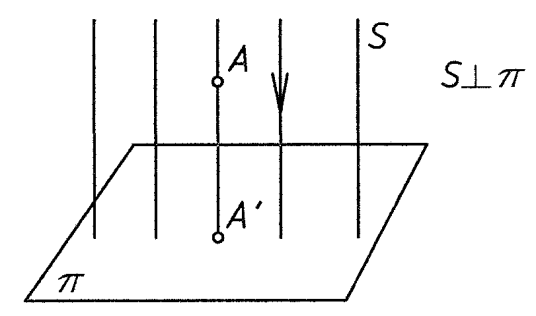
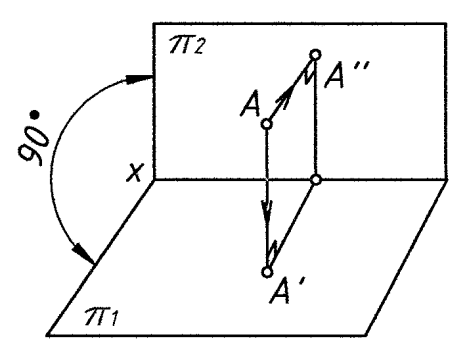
Рис. 3
Свойства прямоугольного проецирования
Проекция точки есть точка.
В общем случае проекция прямой есть прямая линия; проекция кривой линии есть кривая (сохраняет порядок кривой).
Свойство принадлежности фигур Ф и Ф1. Если
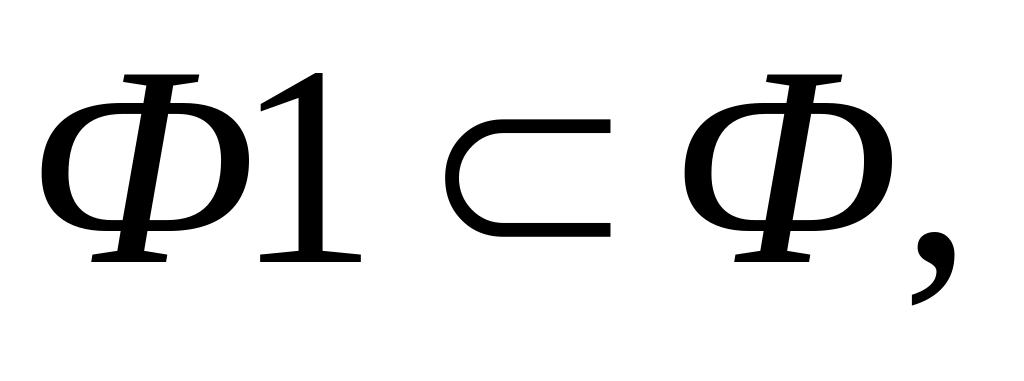то
Параллельные прямые проецируются в параллельные прямые.
Сохраняется простое отношение 3-х точек, т.е.
Следствия:
Если плоская фигура параллельна плоскости проекций, то она проецируется на эту плоскость без искажений.
При параллельном переносе плоскости проекций в направлении проецирования проекции фигуры остаются неизменными.