
- •1 Основные понятия теории вероятностей. Теоремы сложения и умножения вероятностей. Условная вероятность события
- •2 Функция распределения случайной величины
- •3 Плотность вероятности, формула плотности вероятности
- •4 Числовые характеристики случайных величин, их статистические и вероятностные значения. Центрированные случайные величины. Некоррелированные случайные величины
- •5 Равномерное распределение плотности вероятности
- •6 Нормальное (Гауссово) распределение плотности вероятности
- •7 Показательное распределение случайных величин
- •8 Закон распределения Рэлея, Вейбулла и Пуассона
- •9 Основные понятия теории надежности, определение надежности. Пути повышения надежности
- •10 Терминология теории надежности. Определение восстанавливаемых и невосстанавливаемых изделий, простых и сложных изделий. Определение эффективности работы изделия
- •11 Отказы и их виды
- •12 Надежность (безотказность) невосстанавливаемого изделия, функция надежности
- •14 Период нормальной эксплуатации. Экспоненциальный закон надежности, его особенности
- •13 Интенсивность отказов, общая формула вероятности безотказной работы
- •15 Учет влияния износа. Применение нормального закона распределения. Интеграл вероятности и нормальная функция распределения, их применение в расчетах надежности
- •16 Совместное действие внезапных и износовых отказов. Две основные задачи расчета надежности при одновременном действии внезапных и износовых отказов
- •17 Параметрические отказы. Расчет надежности при параметрических отказах
- •18 Условия эксплуатации изделия. Виды нагрузок, действующих на элементы и системы.
- •20 Структурные схемы надежности, определения и исходные условия составления структурных схем.
- •21 Последовательное, параллельное и параллельно-последовательное соединение элементов.
- •22 Способы повышения безотказности элементов. Постоянное резервирование, виды резервирования, кратность резервирования.
- •23 Параллельное включение независимых резервных элементов
- •24 Резервирование замещением, типы резервов
- •25 Резервирование с избирательными схемами (метод голосования)
- •26 Коэффициенты надежности, их классификация. Коэффициент готовности.
- •27 Коэффициент вынужденного простоя, коэффициент профилактики, частота профилактики
- •28 Коэффициент отказов элементов. Относительный коэффициент отказов элементов. Коэффициент расхода элементов
- •29 Частота отказов, средняя частота отказов элементов, их основные свойства. Достоинства и недостатки средней частоты отказов элементов
- •30 Надежность восстанавливаемых систем. Характеристики ремонтопригодности
- •31 Общая надежность изделия
- •32 Методы повышения надежности сложных систем
- •33 Резервирование как средство повышения надежности
- •34 Уменьшение интенсивности отказов
- •35 Сокращение времени непрерывной работы
- •36 Уменьшение среднего времени восстановления
- •37 Спектральный метод расчета надежности при перемежающихся отказах
5 Равномерное распределение плотности вероятности
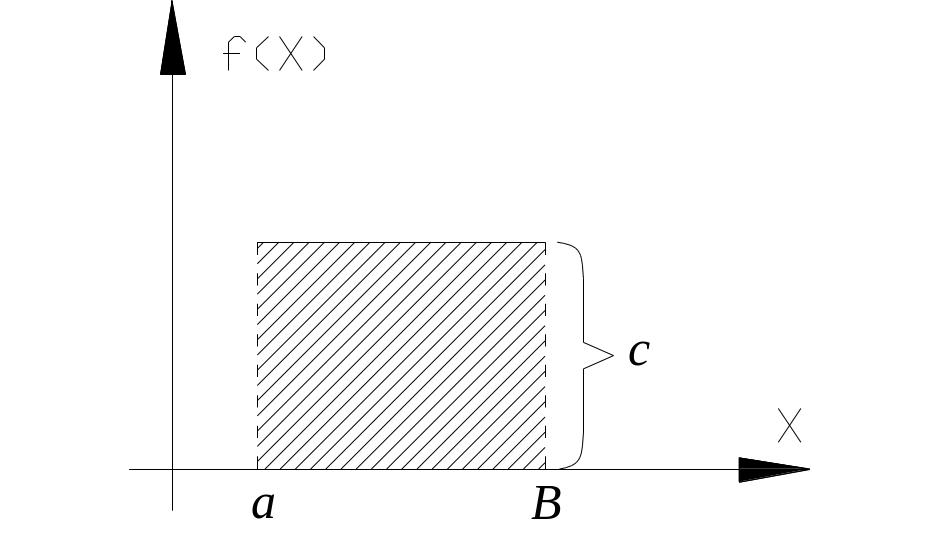 Данное
распределение справедливо в том случае,
если случайное событие лежит в определенном
интервале времени от
Данное
распределение справедливо в том случае,
если случайное событие лежит в определенном
интервале времени от
![]() до
до
![]() и появление его в этом интервале
равновероятно. Поскольку событие
произойдет на интервале времени
и появление его в этом интервале
равновероятно. Поскольку событие
произойдет на интервале времени
![]() отсюда вероятность его появления:
отсюда вероятность его появления:
![]() ,
а
,
а
![]() .
Функция распределения:
.
Функция распределения:
![]() .
Математическое ожидание случайной
величины будет определяться величиной:
.
Математическое ожидание случайной
величины будет определяться величиной:
![]() ,
а дисперсия
,
а дисперсия
![]() .
Дисперсия случайной величины при
равномерном распределении растет
пропорционально квадрату интервала.
Это распределение равномерно.
.
Дисперсия случайной величины при
равномерном распределении растет
пропорционально квадрату интервала.
Это распределение равномерно.
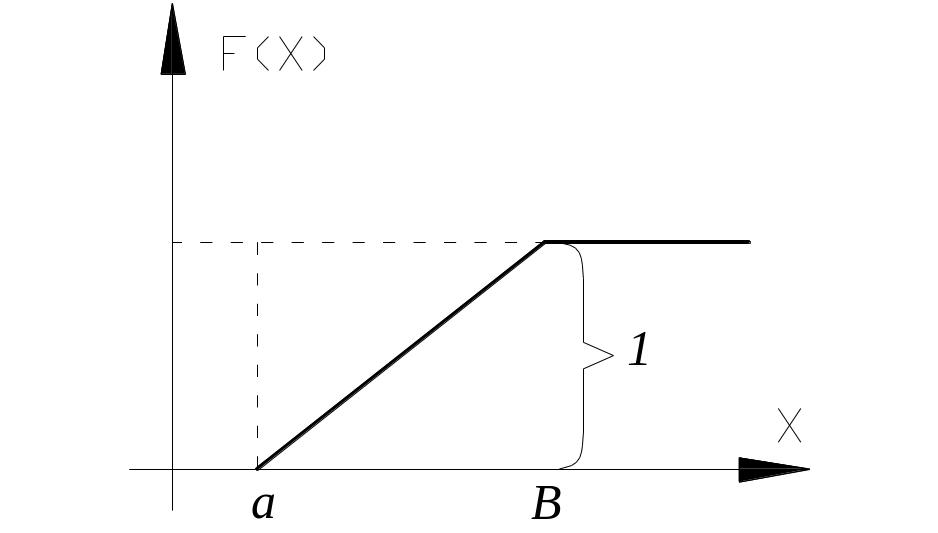 Геометрическая
интерпретация математического ожидания
это координата центра тяжести плоской
фигуры, ограниченной прямой плотности
распределения и абсцисса. Дисперсия
это момент инерции плоской фигуры
относительно оси, проходящей параллельно
оси плотности распределении через центр
тяжести.
Геометрическая
интерпретация математического ожидания
это координата центра тяжести плоской
фигуры, ограниченной прямой плотности
распределения и абсцисса. Дисперсия
это момент инерции плоской фигуры
относительно оси, проходящей параллельно
оси плотности распределении через центр
тяжести.
6 Нормальное (Гауссово) распределение плотности вероятности
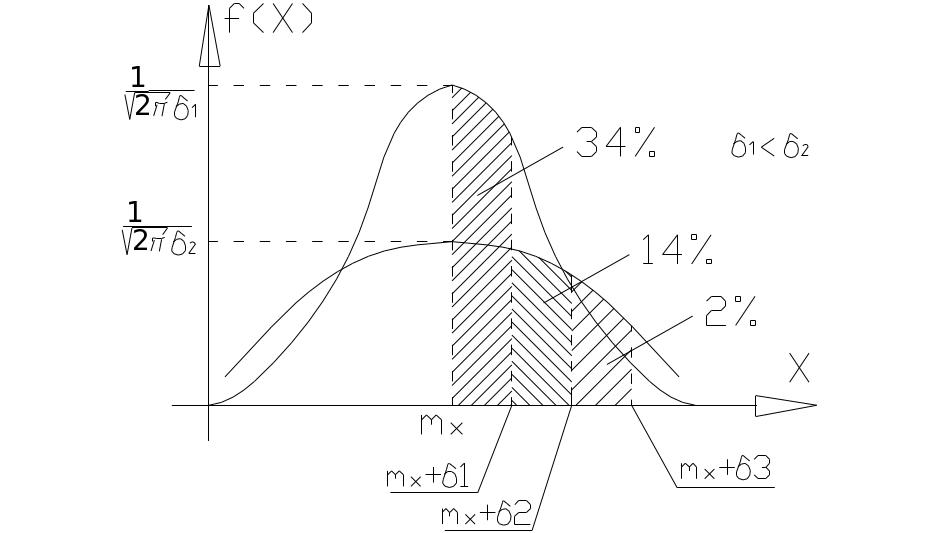 Нормальное
распределение используется в теории
вероятности для описания событий,
зависящих от многих факторов, каждый
из которых слабо влияет на распределение
случайных событий. По нормальному закону
распределяются параметры серийной
продукции, параметры износа. Плотность
распределения:
Нормальное
распределение используется в теории
вероятности для описания событий,
зависящих от многих факторов, каждый
из которых слабо влияет на распределение
случайных событий. По нормальному закону
распределяются параметры серийной
продукции, параметры износа. Плотность
распределения:
![]() .
.
Распределение
Гаусса зависит от двух параметров М(х)
и Д(х). Кривая плотности симметрична
относительно оси, параллельной оси
ординат. Максимальное значение этой
плотности равно
![]() .
Вероятность попадания случайной величины
распределенной по нормальному закону
в заданный интервал
.
Вероятность попадания случайной величины
распределенной по нормальному закону
в заданный интервал
![]() :
:
![]() .
Для упрощения расчета используется
табулированное выражение равенства
(2), вводим новую переменную
.
Для упрощения расчета используется
табулированное выражение равенства
(2), вводим новую переменную
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
.
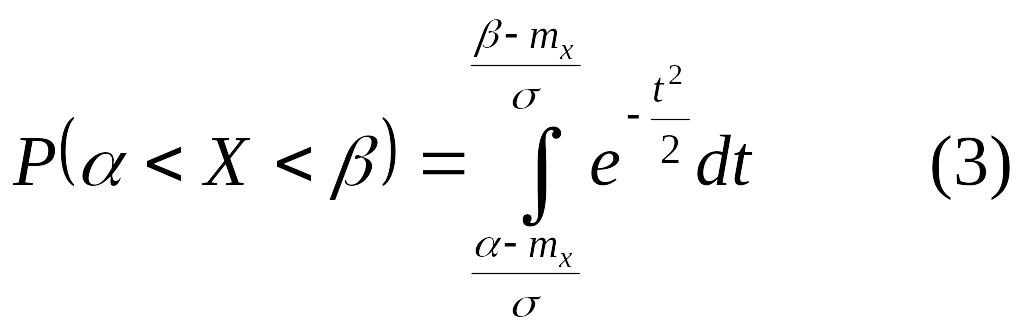 .
.
![]() -
интеграл Лапласа или интеграл вероятности,
тогда
-
интеграл Лапласа или интеграл вероятности,
тогда
![]() .
Интеграл вероятности обладает свойствами:
Ф(0)=0, Ф(
.
Интеграл вероятности обладает свойствами:
Ф(0)=0, Ф(![]() )=0,5,
Ф(-х)=-Ф(х).
)=0,5,
Ф(-х)=-Ф(х).
При
нормальном распределении на интервале
![]() срабатывает закон 3
срабатывает закон 3![]() ,
согласно которому в этом интервале
попадание почти 100%, 97,7%, поэтому вероятность
появления случайной величины вне этого
интервала очень мала, менее 0,3%.
,
согласно которому в этом интервале
попадание почти 100%, 97,7%, поэтому вероятность
появления случайной величины вне этого
интервала очень мала, менее 0,3%.
7 Показательное распределение случайных величин
Это распределение
является наиболее распространенным в
технике из-за своей простоты. Он дает
информацию о распределении отказов
техники, имеющей многоэлементную
структуру. Функция распределения
показательного закона выглядит следующим
образом:
![]() ,
,
![]() .
.
![]()

Дисперсия:
![]() ,
,
![]() .
Свойство (3) часто используется как
основное свойство показательного закона
(в качестве грубой оценке возможности
применения показательных возможностей
её применения на основе полученных
экспериментальных данных)
.
Свойство (3) часто используется как
основное свойство показательного закона
(в качестве грубой оценке возможности
применения показательных возможностей
её применения на основе полученных
экспериментальных данных)
8 Закон распределения Рэлея, Вейбулла и Пуассона
Рэлея. Во многих
прикладных задачах случайные величины
могут принимать только положительные
значения, в этом случае величины
подчиняются закону распределения Рэлея:
![]() .
В этом случае плотнотсь распределения
будет определяться:
.
В этом случае плотнотсь распределения
будет определяться:
 .Математическое
ожидание:
.Математическое
ожидание:
![]() .
Распределение Релея является
однопараметрическим, так как математическое
ожидание и дисперсия связана соотношением
(3). Распределение Релея используется
для ? вероятностных характеристик
колебательных процессов, когда амплитуда
принимается положительная, вибрационные
процессы описываются распределением
Релея.
.
Распределение Релея является
однопараметрическим, так как математическое
ожидание и дисперсия связана соотношением
(3). Распределение Релея используется
для ? вероятностных характеристик
колебательных процессов, когда амплитуда
принимается положительная, вибрационные
процессы описываются распределением
Релея.
Вейбулла. При изучение надежности технических систем часто используется распределение Вейбулла. В основном этот закон используется при описании разбросов усталостной прочности стальных конструкций, конструкций из сплавов.
Функция распределения:
![]() ,
если к=1 – показательный закон
распределения.
,
если к=1 – показательный закон
распределения.
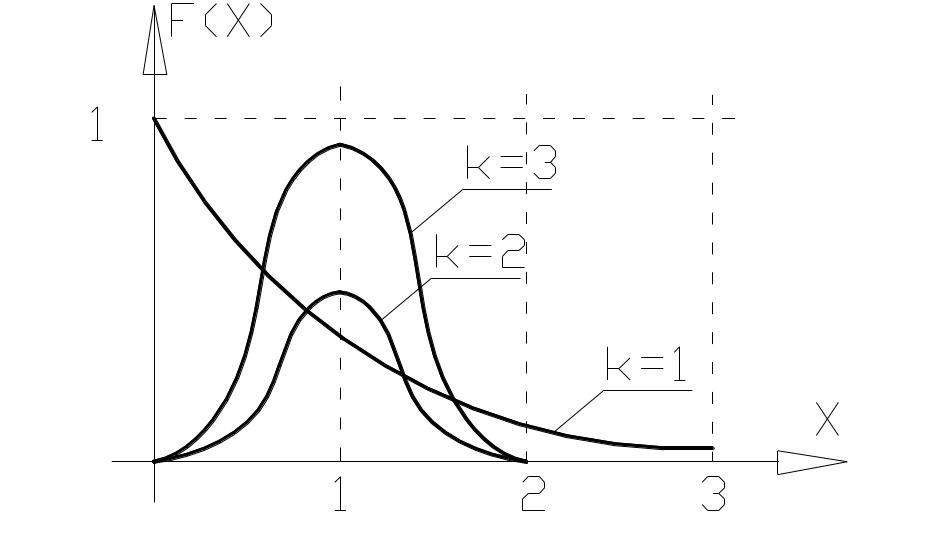 Закон
зависит от
Закон
зависит от
![]() и к.
и к.
Плотность распределения:
![]() .
Согласно (2) закон распределения Вейбулла
зависит от k.
.
Согласно (2) закон распределения Вейбулла
зависит от k.
Пуассона.
Данное распределение является
дискретным и им часто пользуются для
определения вероятности потока событий.
Дискретная случайная величина Х
(безразмерная) называется распределенной
по закону Пуассона если её возможные
значения равны 0, 1, 2, 3…n,
а вероятность того, что x=n
определяется по формуле:
![]() ,
,
![]() Распределение Пуассона обладает тем
свойством, что и мат. Ожидание и дисперсия
равны одной и той же величине.
Распределение Пуассона обладает тем
свойством, что и мат. Ожидание и дисперсия
равны одной и той же величине.
