30 Надежность восстанавливаемых систем. Характеристики ремонтопригодности
Восстанавливаемыми называются изделия или системы, которые в случае возникновения отказа могут быть восстановлены и могут продолжать работать в течение времени от включения…
Для этого интервала времени работы восстанавливаемой системы применены все результаты и выводы, которые применялись для невосстанавливаемых систем. Однако одних характеристик безотказности для восстанавливаемых систем недостаточно, так как элемент изделия восстанавливаются после отказа ремонтируются и продолжают работать поэтому введена характеристика ремонтопригодности.
Характеристики ремонтопригодности. Время восстановления изделия после восстановления зависит:
от вида отказа;
от числа отказавших элементов и т.д.
Эти факторы
носят случайный характер поэтому время
восстановления рассматривают как
случайную величину. Для оценки
ремонтопригодности изделия применяю
вероятностные характеристики: вероятность
выполнения ремонта в заданное время;
интенсивность восстановления
и числовые характеристики
среднее время восстановления (Дв),
.
Вероятность
выполнения ремонта в заданное время
это вероятность того, что отказ изделия
будет устранен в течение заданного
времени в определенных условиях ремонта:
.
Функция (1) называется функцией ремонта.
- вероятность невосстановления. В
реальных условиях любой ремонт не может
быть выполнен мгновенно.
.
Плотность вероятности времени
восстановления называют производную:
.
Интенсивность восстановления
.
Функция (5) – есть условная вероятность
времени восстановления найденная в
предположении, что до момента времени
t изделие находившееся в
ремонте не было восстановлено. Из (5)
следует, что:
.
Левая часть
(6) представляет вероятность
восстанавливаемого изделия на участке
t,t+∆t
– эта вероятность равна произведению
вероятности отказа
на
условную вероятность
.
Из (6) следует:
.
Решения уравнения (7) при условии (3)
определяет выражение для определения
вероятности восстановления изделия в
течение времени t.
На практике
,
тогда (7):
.
Выражение (8) говорит о том, что при
постоянстве
- экспоненциальный закон распределения.
может быть получена экспериментально:
Интервал времени
делится на участки, для каждого i-го
участка определяется
:
,
где
- число изделий время восстановления
или ремонта которых находится на
интервале
,
;
число изделий отремонтированных в
интервал времени 0,
;
N- начальное число
изделий, поставленных на ремонт.
Числовой характеристикой ремонтопригодности является среднее время восстановления, т.е. среднее время вынужденного не регламентируемого простоя, это время складывается из времени начала отказа и время устранения отказа.
Среднее время
восстановления:
,
.
В случае экспоненциального закона
восстановления:
,
,
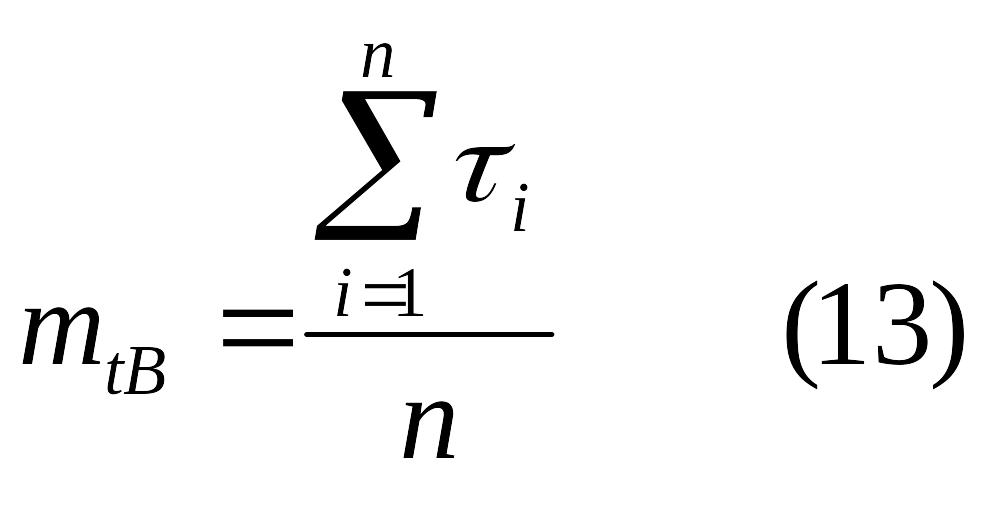где
время, затрачиваемое на обнаружение и
устранение i-го отказа;
n – число отказов за
время наблюдения.
31 Общая надежность изделия
Полной характеристикой надежности восстанавливаемых изделий называется вероятность нормального функционирования или общая надежность. Вероятность того, что система выполнит поставленные задачи зависит: от начального состояния системы; от безотказности и восстанавливаемости и определяется по формуле полной вероятности для сложного события (поток отказа является простейшим).
,
где
вероятность
работоспособного состояния системы в
начальный момент времени, числено равный
коэффициенту готовности;
вероятность
того, что система окажется не работоспособной
к моменту времени её применения;
это
вероятность восстановления (т.е.
обнаружения) устранения отказа и проверки
работоспособности системы а время
;
вероятность
безотказной работы системы за оставшиеся
время
,
которая считается достаточной для
выполнения.
На практике
потому Ро близка к 1 и на практике вторым
слагаемым в равенстве 1 пренебрегают.
.
Равенство (2) определяет вероятность
нормального функционирования системы
как сложного изделия, она определяется
как произведение коэффициента готовности
на вероятность безотказной работы
изделия.