20 Структурные схемы надежности, определения и исходные условия составления структурных схем.

Всякое (неэлементарное) изделие состоит из элементов, тем или иным образом соединенным между собой и взаимодействующих друг с другом. Для расчета надежности изделия необходимо знать характеристики надежности отдельных элементов или цепи узлов.

Структурной надежностью изделия называется результирующая надежность изделия при заданной структуре изделия при известном порядке соединения и известных значениях характеристик и надежности элементов.

В дальнейшем при расчете надежности считается, что характеристики надежности элементов определены и известны. Схемы, изображающие различное соединение элементов – называются структурными схемами.

Структурные схемы надежности составляются:

1.   Элементы системы изображаются в виде прямоугольников. Эти прямоугольники обозначаются номерами или индексами

2.   Одна сторона вход, другая выход;

3.   Элемент считается работающим безотказно, если условный сигнал с входа элемента проходит на его выход , при этом соблюдается однонаправленность в прохождении сигнала;

4.   Отказ элемента означает невозможность передачи через него условного сигнала. Отказ – разрыв цепи передачи;

5.   Линии на структурных схемах, соединяющие прямоугольники считаются безотказными;

6.   Путь передачи сигнала воздействия состоит из последовательно соединенных линий и элементов.

В теории надежности соединение элементов различаются в зависимости от того, как надежность отдельных элементов влияет на результирующую надежность- надежность всего соединения.

Под словом соединения понимается группа или система элементов, соединенных между собой определенным образом: последовательное, параллельное, параллельно-последовательное.

21 Последовательное, параллельное и параллельно-последовательное соединение элементов.

Последовательное соединение элементов- называется такое соединение, при котором отказ одного элемента приводит к отказу остальных элементов.

 

Т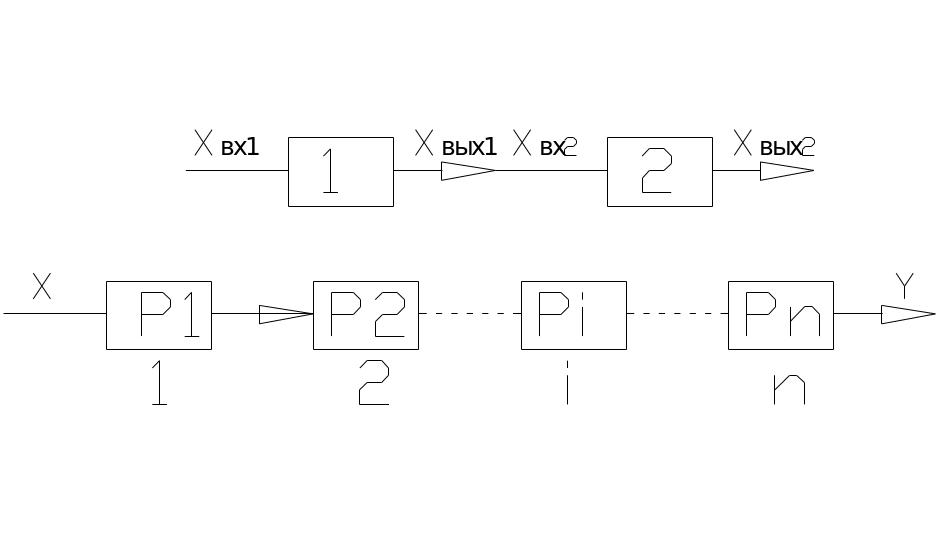 ехническое понятие последовательного соединения может не совпадать с понятием в смысле надежности. Условимся считать, что вероятность безотказной работы одних элементов не зависит от вероятности безотказной работы других элементов, т.е. отказ или изменение одной группы элементов не зависит и не влияет на вероятность безотказной работы других в этом случае элементы называются независимыми, для последовательного соединения элементов вероятность безотказной работы определяется согласно теорем вероятности:

. Согласно (1) результирующая надежность при последовательном соединение есть произведение вероятностей безотказной работы отдельных элементов: . , . Из (2), (3), (4) следует, что при последовательном соединении элементов интенсивности отказов складываются. Интенсивность отказа соединения есть сумма интенсивностей отказов отдельных элементов.

Интенсивность отказа последовательного соединения всегда больше любого из этих элементов. Это приводит к тому, что вероятность безотказной работы последовательного соединения всегда меньше вероятности самого надежного элемента в этой системе.

При экспоненциальном законе надежности: , . Среднее время при экспоненциальном законе надежности: . Если элементы соединения имеют одинаковую интенсивность отказов , то в этом случае вероятность безотказной работы: , где n – число элементов в соединении. Тогда средняя наработка .

Предположим, что требуется найти вероятность безотказной работы соединения из 4-х элементов. 2 из которых имеют экспоненциальную функцию надежности, а 2 – подчиняются закону Вейбулла.

- экспоненциальный закон надежности;

- закон распределения Вейбулла.

Тогда суммарная безотказность работы всего соединения будет равна:

, , если подставить в последнее равенство , то можно найти вероятность безотказной работы соединения.

Может быть решена и обратная задача. Пусть задана вероятность безотказной работы. Требуется определить какая допустимая при этом суммарная интенсивность. Все элементы имеют экспоненциальный закон надежности. , , .

 

Параллельное в смысле надежности называется такое соединение элементов, когда отказ всего соединения наступит тогда, когда отказывают все элементы, входящие в соединение.

При расчете надежности предполагается, что элементы являются независимыми, т.е. отказ одного из них не влияет на работу других.

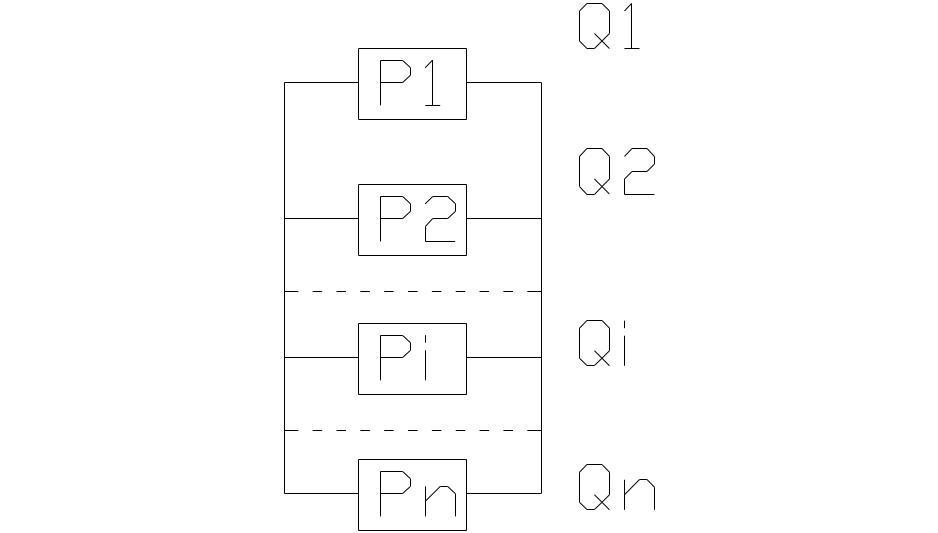
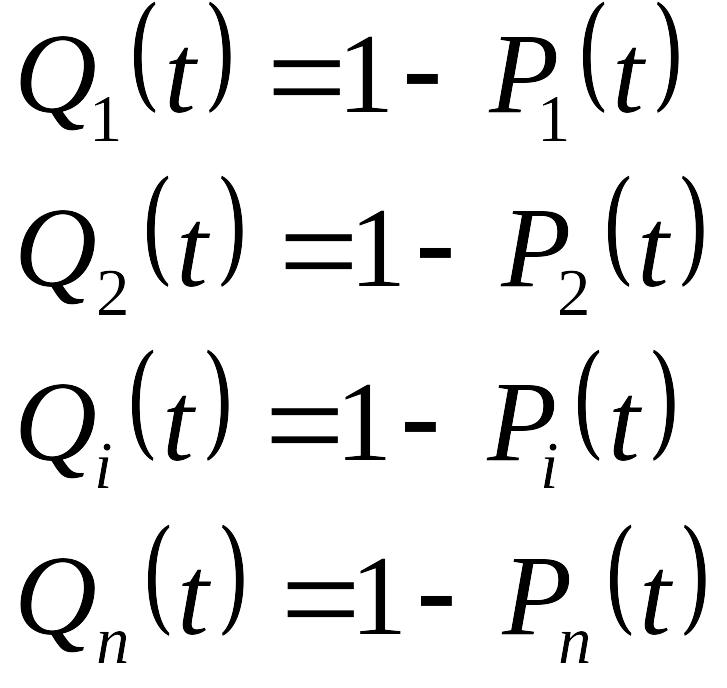
Вероятность отказа всего соединения произойдет в случае отказа всего соединения: , Вероятность отказа системы согласно (1) равна произведению отказов всех его элементов. Вероятность безотказной системы: . В случае когда вероятность безотказной работы отдельных элементов подчиняются экспоненциальному закон надежности:

. Из (4) следует, что функция надежности параллельного соединения элементов, в отличие от последовательного соединения, при экспоненциальной функции отдельных элементов уже не является экспоненциальным законом, если функции надежности элементов одинаковы. , , , .

При экспоненциальном законе надежности: , , , . Математическое ожидание при экспоненциальном законе надежности:

. Если продолжительность времени работы системы не велико, так что произведение интенсивностей отказов на время работы много меньше 1, то можно считать: , , тогда сохраняя два первых члена в разложении экспоненты получим, что вероятность безотказной работы равна: , .

 

Параллельно-последовательное соединение элементов. Наиболее распространенными являются 2 схемы параллельно- последовательного соединения.

В 1 –ой схеме имеется m параллельных цепей по n одинаковых элементов в каждой цепи. Элементы как и прежде считаются независимыми.

Вероятность безотказной работы каждой j цепи: . Вероятность безотказной работы всей схемы: .

Во второй схеме n последовательно соединенных групп, состоящие из m одинаковых параллельно соединенных элементов. . Тогда для всей схемы: . В большинстве случаев при практических расчетах сложные схемы можно разбить на части, состоящие из простейших соединений. При составлении структурной схемы надежности в качестве отдельных элементов могут быть взяты элементарные звенья или целые узлы. Если у этих узлов известны характеристики надежности.