Вариант 17

1. На группу из 10 юношей и 15 девушек выделили 8 билетов в театр. Какова вероятность, что при случайном распределении билетов в группе «театралов» окажется поровну юношей и девушек?

2. Три охотника выстрелили в гуся. Вероятности их попаданий таковы: 0,7; 0,8; 0,6. Найти вероятности событий:

а) гусь уцелеет;

б) в него попадет только один охотник;

в) попадет хотя бы один охотник.

3. Два рабочих производят однотипные детали, при этом производительность первого в два раза больше, чем у второго. У первого рабочего получается в среднем 2% брака, у второго – 1%. Контролер обнаружил бракованную деталь. Каким вероятнее рабочим она изготовлена?

4. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,6. Найти наивероятнейшее число поступивших заявок на снабжение в данный день и его вероятность.

5. Вероятность рождения мальчика равна 0,515. Найти вероятность того, что среди 1 000 новорожденных будет:

а) 480 девочек;

б) девочек больше половины.

6. Оценить, сколько нужно проверить изделий, чтобы с вероятностью 0,98 можно было ожидать, что абсолютная величина отклонения относительной частоты годности изделия от вероятности 0,9 изделия быть годным не превысила 0,01.

7. Бросают три игральных кубика. Составить закон распределения числа выпавших «шестерок» на трех кубиках. Найти математическое ожидание и дисперсию этой случайной величины.

8. Непрерывная случайная величина X задана плотностью распределения f (х) = (3/2) sin Зх в интервале (0, /3); вне этого интервала f(x) = 0. Найти вероятность того, что X примет значение, принадлежащее интервалу (/6, /4).

Вариант 18

1. В шахматном турнире участвуют 20 человек, которые по жребию распределяются в две группы по 10 человек. Определить вероятность того, что два наиболее сильных игрока будут играть в разных группах.

2. Вероятности сдачи экзамена по математике для трех данных студентов таковы: 0,9; 0,85; 0,8. Найти вероятности следующих событий:

а) только один из этих студентов сдаст экзамен;

б) не сдаст ни один;

в) хотя бы один студент сдаст экзамен.

3. В обследуемой группе мужчин некоторого возраста 60% курящих, а остальные – некурящие. В среднем 30% курящих этого возраста имеют заболевания легких, у некурящих – 5%. Вычислить вероятность того, что случайно обследуемый мужчина этого возраста имеет заболевание легких.

4. В цехе работает 120 рабочих, при этом 75% из них перевыполняют месячный план. Найти наивероятнейшее число перевыполняющих месячный план рабочих и соответствующую ему вероятность.

5. Вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,04. Вычислить вероятность того, что в течение гарантийного срока из 200 телевизоров:

а) не более одного потребуют ремонта;

б) хотя бы один телевизор потребует ремонта.

6. С конвейера сходит в среднем 80% изделий первого сорта. Сколько изделий необходимо взять, чтобы с вероятностью 0,996 гарантировать, что по абсолютной величине отклонение относительной частоты от вероятности изделия первого сорта не превысит 0,01?

7. Устройство состоит их трех независимо работающих элементов. Вероятность отказа каждого элемента 0,15. Составить закон распределения отказавших элементов. Найти математическое ожидание и дисперсию этой случайной величины.

8. Дана функция распределения непрерывной случайной величины X:

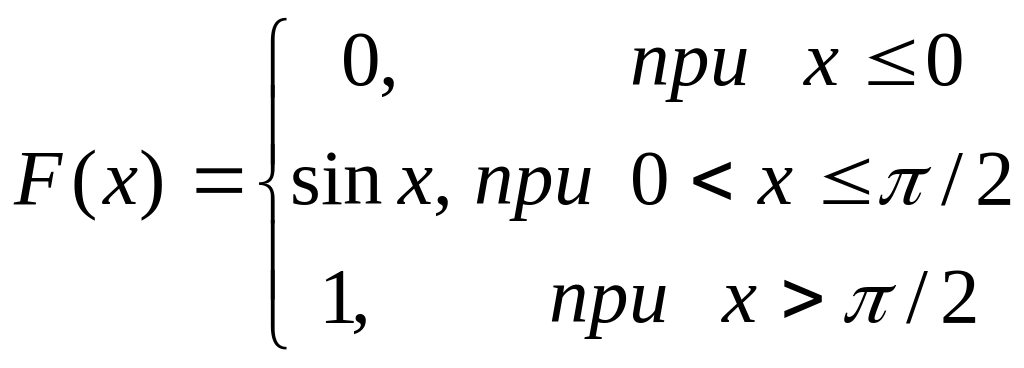
Найти плотность распределения f(x).