Вариант 9
1. Код банковского сейфа состоит из 6 цифр. Найти вероятность «взломать» сейф, если взломщик знает:
а) первые три цифры кода;
б) что все цифры кода различные.
2. Вероятность отказа за время Т первого элемента равна 0,4; для второго – 0,2; для третьего – 0,1. Найти вероятности безотказной работы цепи за время Т. Схема включения элементов цепи приведена на рисунке:
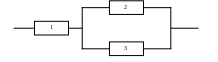
3. Вероятность, что безработный найдет работу, обратившись в службу занятости, равна 0,3. Оценить вероятность того, что среди 12 человек, обратившихся за день, работу найдут пять. Чему равна вероятность того, что из 320, обратившихся за месяц, работу получат от 100 до 200?
4.
При исследовании больного имеется
подозрение на одно из трех заболеваний:
А1,
А2,
А3.
Их вероятности (по мнению врача)
соответственно равны:
.
Для уточнения диагноза назначен анализ,
дающий положительный результат с
вероятностью 0,1 в случае заболевания
А1,
с вероятностью 0,2 в случае заболевания
А2
и с вероятностью 0,9 в случае заболевания
А3.
Анализ был произведен пять раз и дал
четыре раза положительный результат и
один раз отрицательный. Требуется найти
вероятность каждого заболевания после
анализа.
5. Вероятность несчастного случая за год равна 0,0003 для жителя. Застраховано 10 000 человек. Общий фонд страхования равен 1 000 000 руб. Страховая выплата равна 200 000 руб. Какова вероятность «разорения» фирмы?
6. Монета подбрасывается 200 раз. Найти вероятность того, что относительная частота появления «герба» отклонится от его вероятности по абсолютной величине не более чем на 0,02.
7. Среди 10 изготовленных приборов 3 неточных. Составить закон распределения числа неточных приборов среди взятых наудачу четырех приборов. Найти дисперсию этой случайной величины.
8. Случайная величина Х задана плотностью вероятности f(x) = х/2 в интервале (0; 2), вне этого интервала f(x) = 0. Найти математическое ожидание величины Х.
Вариант 10
1. Первенство по баскетболу оспаривают 18 лучших команд, которые путем жеребьевки распределяются на две группы по 9 команд в каждой. Пять команд обычно занимают первые места. Какова вероятность попадания всех лидирующих команд в одну группу? Какова вероятность попадания двух лидирующих команд в одну группу и трех – в другую?
2. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если для второго орудия эта вероятность равна 0,8.
3. Имеется 30 билетов, из которых данный студент знает 25. У студента есть две возможности: взять билет первым или, уступив очередь, вторым. В каком случае вероятность успешной сдачи выше?
4. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3 – шатеном, с вероятностью 0,4 – блондином и с вероятностью 0,1 – рыжим. Найти вероятность того, что среди шести случайно встреченных лиц:
а) не менее 4 блондинов;
б) хотя бы один рыжий;
в) 3 блондина и 3 шатена.
5. Среди 1 000 человек приблизительно 8 левшей. Найти вероятность того, что среди сотни наугад выбранных человек:
а) будет хотя бы один левша;
б) не окажется ни одного левши;
в) левшей будет от одного до трех.
6. Вероятность того, что студент воспользуется услугами банкомата, равна 0,1. Оценить, что услугами банкомата воспользуются от 15 до 25 человек из 200 студентов. Найти вероятность того, что отклонение числа студентов, которые воспользуются банкоматом, от наивероятнейшего числа не превзойдет трех.
7. Ряд распределения дискретной случайной величины состоит из двух неизвестных значений. Вероятность того, что случайная величина примет одно из этих значений, равна 0,8. Найти функцию распределения случайной величины, если ее математическое ожидание равно 3,2, а дисперсия 0,16.
8. Случайная величина Х задана плотностью вероятности f(x) = х/8 в интервале (0; 4). Вне этого интервала f(x) = 0. Найти математическое ожидание величины Х.