Вариант 5

1. Подсчитать вероятность того, что в наудачу выбранном телефонном номере, состоящем из 6 цифр, все цифры окажутся различными.

2. Рабочий обслуживает три станка. Вероятность того, что в течение смены потребует его внимания первый станок, равна 0,7; второй – 0,75; третий – 0,8. Найти вероятность того, что в течение смены внимания рабочего потребуют:

а) какие-либо два станка; б) хотя бы один станок.

3. Изделия изготавливаются на трех станках-автоматах. Первый производит 40%, второй – 50%, а третий 10% всех изделий. Брак в их продукции составляет соответственно 3%, 4%, 1%. Случайно выбранное изделие оказалось стандартным. Найти вероятность того, что оно произведено:

а) первым станком-автоматом;

б) вторым станком-автоматом.

4. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Найти вероятность того, что из пяти первых покупателей обувь этого размера будет необходима:

а) одному покупателю;

б) по крайней мере одному.

5. Вероятность получения с конвейера изделия первого сорта равна 0,9. Определить вероятность того, что из 500 изделий, взятых на проверку:

а) 460 будут первого сорта;

б) от 400 до 480 (включительно) будут первого сорта.

Найти наивероятнейшее число изделий первого сорта среди 500 изделий.

6. Сколько нужно произвести опытов с бросанием монеты, чтобы с вероятностью 0,92 можно было ожидать, что отклонение относительной частоты выпадения «герба» от вероятности выпадения «герба» по абсолютной величине будет меньше 0,1?

7. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено 4 ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание и дисперсию этой случайной величины.

8. Случайная величина Х имеет плотность вероятности:

Найти функцию распределения вероятностей и построить график.

Вариант 6

1. На полке наугад расставлены 18 книг. Найти вероятность того, что:

а) три тома одного сочинения окажутся поставленными вместе в порядке номеров;

б) три тома будут поставлены вместе.

2. Вероятность отказа за время Т для первого элемента равна 0,1; для второго – 0,2; для третьего – 0,15. Найти вероятность безотказной работы цепи за время Т. Схема включения элементов цепи приведена на рисунке:

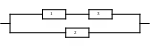
3. На сборку поступило 3 000 деталей с первого автомата и 2 000 со второго. Первый автомат дает 0,27% брака, а второй – 0,33%. Найти вероятность попадания на сборку бракованной детали, если деталь выбирается наудачу из всех деталей. Найти вероятность того, что взятая наудачу деталь изготовлена первым автоматом, если при проверке она оказалась стандартной.

4. Производится 6 выстрелов по цели. Вероятность попадания при каждом выстреле равна 0,7. Найти вероятность того, что:

а) произойдет одно попадание в цель;

б) произойдет не менее пяти попаданий;

в) произойдет хотя бы одно попадание.

5. В осветительную сеть включено 1 100 новых электроламп. Вероятность того, что в течение года электролампа перегорит, равна 0,55. Найти вероятность того, что в течение года не менее половины ламп придется заменить новыми. Найти наивероятнейшее число перегоревших электроламп.

6. Вероятность поражения мишени при одном выстреле равна 0,6. Найти число выстрелов по мишени, чтобы с вероятностью 0,993 ожидать, что отклонение частости от вероятности 0,6 будет меньше 0,03 (по абсолютной величине).

7. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составить закон распределения числа таких договоров среди наудачу выбранных четырех. Вычислить математическое ожидание и дисперсию этой случайной величины.

8. Найти функцию распределения вероятностей и построить график, если случайная величина Х имеет плотность вероятности: .
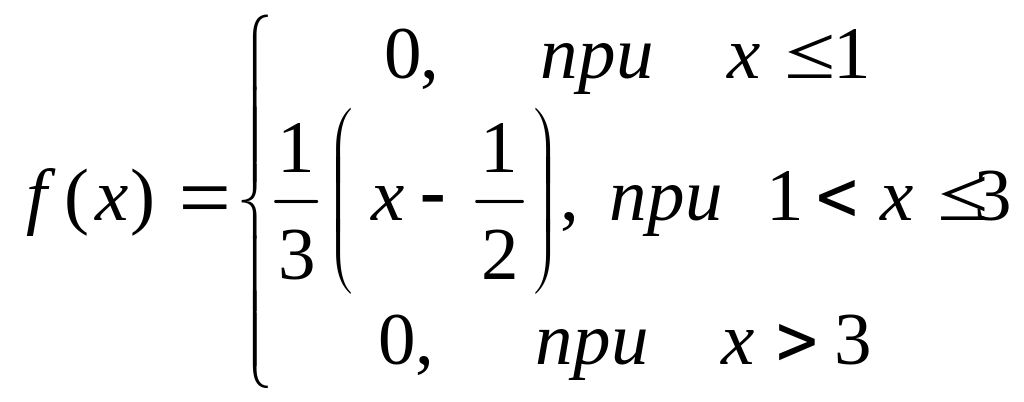