Вариант 19
1. Группа из десяти мужчин и десяти женщин делится случайно на две равные части. Какова вероятность того, что в каждой из частей мужчин и женщин будет поровну?
2. Два спортсмена выполняют норму мастера спорта. Вероятность выполнения нормы для первого спортсмена равна 0,8, а для второго – 0,7. Найти вероятности следующих событий:
а) норму выполнит только один какой-нибудь спортсмен;
б) не выполнит ни один;
в) выполнит хотя бы один спортсмен.
3. В первой урне имеется 10 белых и 5 красных шаров, во второй – 8 белых и 10 красных, в третьей – 6 белых и 6 красных. Выбирающий наугад подошел к одной из урн и наугад взял один шар. Вычислить вероятность того, что этот шар оказался красным.
4. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть: две партии из четырех или три из шести?
5. Всхожесть семян данной культуры характеризуется вероятностью 0,8. Для контроля всхожести посеяли 500 семян. Найти вероятности следующих событий:
а) взойдет не более половины посеянных;
б) взойдет не менее 400.
Найти наивероятнейшее число взошедших семян среди 500 посеянных.
6. Оценить вероятность того, что в партии из 10 000 подшипников отклонение относительной частоты брака от вероятности подшипнику быть бракованным, равной 0,01, не превысит по абсолютной величине 0,03.
7. Вероятность того, что при составлении бухгалтерского баланса допущена ошибка, равна 0,3. Аудитору на заключение представлено 3 баланса предприятия. Составить закон распределения числа положительных заключений на проверяемые балансы. Найти математическое ожидание и дисперсию этой случайной величины.
8. Случайная величина Х задана функцией распределения:
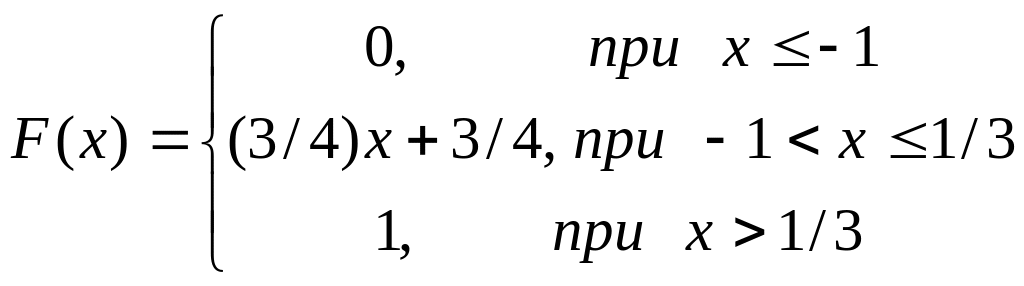
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0; 1/3).
Вариант 20
1. Колоду из 36 карт наугад разделили на две равные части. Какова вероятность того, что в каждой из частей будет поровну карт черных и красных мастей?
2. В среднем 80% саженцев яблони и 90% саженцев груш приживались при посадке. На садовом участке будет посажено по одному саженцу каждой культуры. Найти вероятности следующих событий:
а) приживется только один из саженцев;
б) приживутся оба;
в) приживется хотя бы один саженец.
3. Три мальчика с одинаковыми корзинами собирали в лесу грибы. Первый нашел 5 белых и 10 подосиновиков, второй – 8 белых и 10 подосиновиков, третий – 6 белых и 8 подосиновиков. При встрече они составили корзины вместе. Через некоторое время первый мальчик случайно взял с одной из корзин белый гриб. Какова вероятность того, что он взял этот гриб со своей корзины?
4. Жюри состоит из пяти членов, каждый из которых выносит верное решение с вероятностью 0,9. Вычислить вероятность, что жюри вынесет верное решение, если оно принимается большинством членов.
5. Вероятность нарушения герметичности консервной банки равна 0,0004. Найти вероятность того, что из 5 000 банок герметичность нарушится:
а) у двух банок;
б) не меньше чем у двух банок.
6. Вероятность поражения мишени стрелком при одном выстреле равна 0,6. Оценить вероятность того, что при 600 выстрелах число попаданий в мишень будет по абсолютной величине отличаться от наивероятнейшего числа попаданий не более чем на 25.
7. Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса, равна 0,05. Аудитору на проверку представлено 2 баланса. Составить закон распределения числа правильных заключений на проверяемые балансы. Найти математическое ожидание и дисперсию этой случайной величины.
8. Дискретная случайная величина X задана законом распределения:
X 2 4 7
р 0,5 0,2 0,3
Найти функцию распределения F (х) и начертить ее график.