Задание №7. Лемешев с.

К ороткая цилиндрическая оболочка радиуса R, длины L и толщины h нагружена внутренним давлением р. По правому торцу оболочка закреплена шарнирно, а по левому – защемлена. Найдите аналитически перемещения и внутренние силовые факторы в оболочке. Числовые значения возьмите из таблицы.

	R[м]	L[м]	h[мм]	p[МПа]	E[МПа]	µ
1	1.00	0.50	1.75	0.01

Нужно найти общее решение дифференциального уравнения

Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.

Общее решение однородного уравнения.

Характеристическое уравнение , где

Корни характеристического уравнения : ; ; ; .

Решение, соответствующее найденным корням

Общее решение неоднородного уравнения

Это решение нужно подчинить граничным условиям. При : и ; при : и

Задание №8. Рызбаев р.

К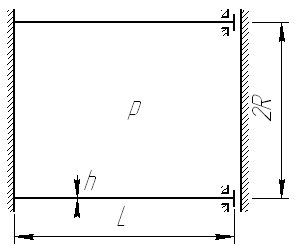 ороткая цилиндрическая оболочка радиуса R, длины L и толщины h нагружена внутренним давлением р. По левому торцу оболочка защемлена, по правому – «скользящая заделка». Найдите аналитически перемещения и внутренние силовые факторы в оболочке. Числовые значения возьмите из таблицы.

	R[м]	L[м]	h[мм]	p[МПа]	E[МПа]	µ
1	1.00	0.50	1.75	0.01

Нужно найти общее решение дифференциального уравнения

Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.

Общее решение однородного уравнения.

Характеристическое уравнение , где

Корни характеристического уравнения : ; ; ; .

Решение, соответствующее найденным корням

Общее решение неоднородного уравнения

Это решение нужно подчинить граничным условиям. При : и ; при : и

Задание №9. Сафронова т.

К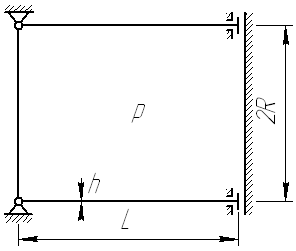 ороткая цилиндрическая оболочка радиуса R, длины L и толщины h нагружена внутренним давлением р. По левому торцу оболочка закреплена шарнирно, по правому – «скользящая заделка». Найдите аналитически перемещения и внутренние силовые факторы в оболочке. Исходные данные возьмите из таблицы.

	R[м]	L[м]	h[мм]	p[МПа]	E[МПа]	µ
1	1.00	0.50	2.00	0.01

Нужно найти общее решение дифференциального уравнения

Частное решение неоднородного уравнения обозначим . Частное решение ищем в виде константы , подставляя в дифференциальное уравнение получим: , откуда: – это решение совпадает с решением по безмоментной теории.

Общее решение однородного уравнения. Характеристическое уравнение , где

Корни характеристического уравнения: ; ; ; .

Решение, соответствующее найденным корням

Общее решение неоднородного уравнения

Это решение нужно подчинить граничным условиям. При : ; ; при ;