
Задание №1. Зверев н.

Полубесконечная цилиндрическая оболочка, шарнирно опертая по левому торцу, нагружена внутренним давлением р, толщина оболочки h, радиус срединной поверхности R. Используя теорию краевого эффекта, постройте эпюры перемещений и изгибающих моментов вблизи левого торца. Исходные данные возьмите из таблицы.
|
R[м] |
h[мм] |
p[МПа] |
E[МПа] |
µ |
1 |
1.00 |
1.75 |
0.01 |
|
|
Нужно найти общее решение дифференциального уравнения
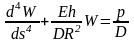
Частное решение
неоднородного уравнения обозначим
 .
Частное решение ищем в виде константы
.
Частное решение ищем в виде константы
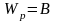 ,
подставляя в дифференциальное уравнение
получим:
,
подставляя в дифференциальное уравнение
получим:
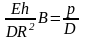 ,
откуда:
,
откуда:
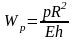 – это решение совпадает с решением по
безмоментной теории.
– это решение совпадает с решением по
безмоментной теории.
Общее решение однородного уравнения.
Характеристическое
уравнение
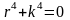 ,
где
,
где

Корни характеристического
уравнения :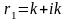 ;
;
 ;
;
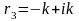 ;
;
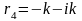 .
.
Решение, соответствующее найденным корням
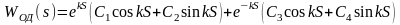
Общее решение неоднородного уравнения

Это решение нужно
подчинить граничным условиям. На
бесконечности условие ограниченности
решения. При
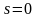 :
:
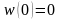 ;
;

Задание №2. Кожевников м.
Ц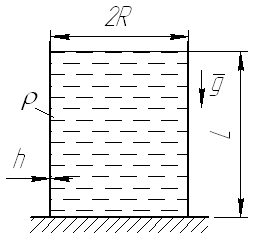 илиндрическая
оболочка длиной L
и радиуса R
заполнена до краев жидкостью плотности
ρ,
толщина оболочки h.
По нижнему торцу оболочка закреплена
неподвижно. Используя теорию краевого
эффекта, определите перемещения и
внутренние силовые факторы вблизи
нижнего торца. Числовые данные возьмите
из таблицы.
илиндрическая
оболочка длиной L
и радиуса R
заполнена до краев жидкостью плотности
ρ,
толщина оболочки h.
По нижнему торцу оболочка закреплена
неподвижно. Используя теорию краевого
эффекта, определите перемещения и
внутренние силовые факторы вблизи
нижнего торца. Числовые данные возьмите
из таблицы.
|
R[м] |
L[м] |
h[мм] |
ρ[кг/м3] |
E[МПа] |
µ |
1 |
1.00 |
10.00 |
1.75 |
1000 |
|
|
Усилия
 и
и
 находим
из условий равновесия. В продольном
направлении нагрузок нет, следовательно,
находим
из условий равновесия. В продольном
направлении нагрузок нет, следовательно,
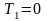 .
Распределенная нагрузка
.
Распределенная нагрузка
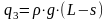 - это гидростатическое давление. Из
уравнения Лапласа усилие
- это гидростатическое давление. Из
уравнения Лапласа усилие

 .
Используя физические уравнения найдем
деформации
.
Используя физические уравнения найдем
деформации
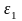 и
и
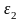 :
:
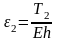 ,
,

Из геометрических уравнений для осесимметричной деформации цилиндрической оболочки
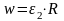 ,
,
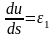
Из этих уравнений
находим перемещения
 и
и
 .
Для
удовлетворяем граничным условиям в
шарнире. В окрестности шарнирного
закрепления используем уравнения
краевого эффекта. Решение по безмоментной
теории для
рассматриваем как частное решение для
уравнения краевого эффекта.
.
Для
удовлетворяем граничным условиям в
шарнире. В окрестности шарнирного
закрепления используем уравнения
краевого эффекта. Решение по безмоментной
теории для
рассматриваем как частное решение для
уравнения краевого эффекта.
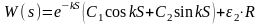 ,
,
где
.
Константы
 и
и
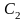 находим
из граничных условий при
:
находим
из граничных условий при
:
 и
и
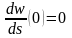 .
.
Задание №3. Королева а.
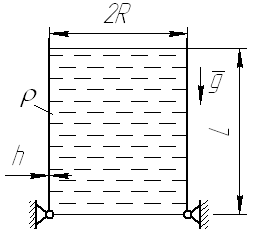
Цилиндрическая оболочка длиной L и радиуса R заполнена о краев жидкостью плотности ρ, толщина оболочки h. По нижнему торцу оболочка закреплена шарнирно. Используя теорию краевого эффекта, определите перемещения и внутренние силовые факторы вблизи нижнего торца. Числовые данные возьмите из таблицы.
|
R[м] |
L[м] |
h[мм] |
ρ[кг/м3] |
E[МПа] |
µ |
1 |
1.00 |
10.00 |
1.75 |
1000 |
|
|
Усилия и находим из условий равновесия. В продольном направлении нагрузок нет, следовательно, . Распределенная нагрузка - это гидростатическое давление. Из уравнения Лапласа усилие . Используя физические уравнения найдем деформации и :
,
Из геометрических уравнений для осесимметричной деформации цилиндрической оболочки
,
Из этих уравнений находим перемещения и . Для удовлетворяем граничным условиям в шарнире. В окрестности шарнирного закрепления используем уравнения краевого эффекта. Решение по безмоментной теории для рассматриваем как частное решение для уравнения краевого эффекта.
,
где . Константы и находим из граничных условий при : и .
