Фазовая манипуляция

При цифровой фазовой манипуляции (ФМн, англ. PSK - phase-shift keying) фаза высокочастотного манипулированного колебания может принимать конечное число разных значений. В простейшем случае, при двоичной фазовой манипуляции в качестве таких значений обычно выбирают 0° и 180°. На рис. 3.7 показан пример фазоманипулированного колебания, фаза которого, принимает значения 0° и 180° в моменты изменения полярности управляющего биполярного сигнала, представляющего собой комбинацию двоичных единиц и двоичных нулей.

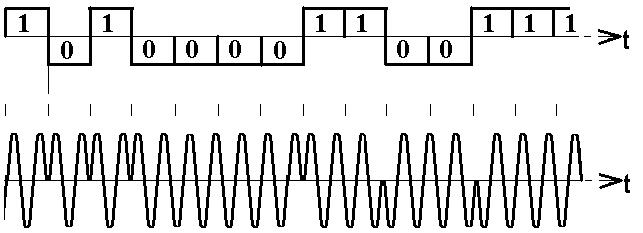
Рис. 3.7 Пример фазоманипулированного сигнала

На рис. 3.8 приведен спектр двоичного ФМн сигнала [14]. Как видим, составляющая на несущей частоте f отсутствует.

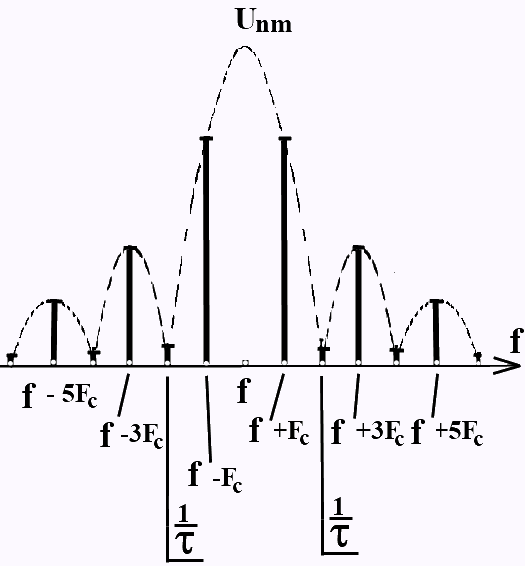
Рис. 3.8 Спектр фазоманипулированного сигнала (двоичная ФМн)

Причиной этому является следующее. Временную диаграмму ФМн сигнала (рис. 3.7) можно представить в виде двух последовательностей радиоимпульсов с одинаковой частотой следования F_c, одинаковым значением несущей частоты, но противоположными значениями начальных фаз. Спектральная диаграмма ФМн сигнала является результатом наложения 2-х спектров, каждый из которых, соответствует своей последовательности радиоимпульсов. Для выбранных значений скачков фазы (180°) и при скважности T_c/τ_и = 2, вся энергия сигнала содержится только в боковых полосах, т.е. составляющая на несущей частоте отсутствует.

Амплитуды боковых составляющих в 2 раза больше, чем у АМн сигналов, что обуславливает большую помехоустойчивость этого вида манипуляции перед АМн.

Ширина спектра ФМн сигнала, по аналогии со спектром АМн сигнала, также определяется в зависимости от длительности информационного импульса τ_и. Например, для длительности импульса τ_и = 15,6 мкс (см. пример для ЧМн сигнала, где ΔF_ЧМн = 388 кГц), ширина спектра составит: ΔF_ФМн = 2·1/τ = 2/15,6·10^-6 = 64 кГц.

Как видим, ширина спектра ФМн сигнала значительно уже ширины спектра ЧМн сигнала. Следовательно, для передачи ФМн сигналов требуется более узкая полоса пропускания канала связи, либо при той же полосе пропускания канала связи можно передавать ФМн сигналы с большей скоростью, нежели ЧМн сигналы.

Помехоустойчивость канала связи ФМн соответственно выше, чем у ЧМн.

Квадратурная фазовая манипуляция

При квадратурной фазовой манипуляции (англ. QPSK - uadrature phase shift keying) модуляция строится на основе кодирования двух бит передаваемой информации одной фазе высокочастотного колебания. На рис.3.9 показана данная процедура.

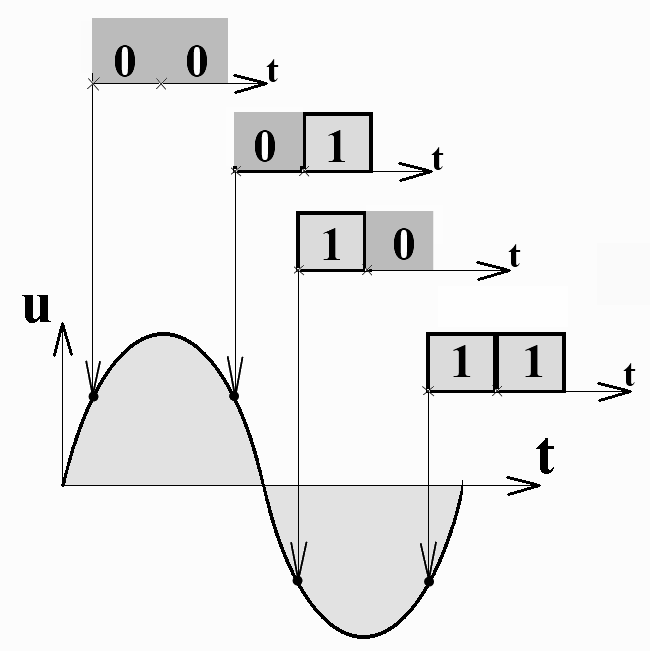
Рис. 3.9 К понятию квадратурной фазовой манипуляции (QPSK)

Каждой паре информационных импульсов соответствует своя фаза высокочастотного колебания: 00 - 45º; 01 - 135º; 10 - 225º; 11 - 315º. Аналогично предыдущему, для передачи трехбитового слова (000, 001, 010 и т.д) нужно применить восемь значений фаз, для четырехбитового слова (0000,0001,0010 и т.д.) - 16 значений фазовых углов.

А теперь, в качестве обобщения по рассмотренным способам манипуляции, решим следующую задачу.

Имеется канал связи, полоса пропускания которого 200 кГц (спутниковые системы связи VSAT и Инмарсат BGAN (§5.22)).

Требуется определить возможную скорость передачи информации по такому каналу для АМн, ЧМн и ФМн сигналов. Ширину спектров сигналов принять на уровне 1/τ.

Решение:

Для АМн сигнала. Ширина спектра сигнала должна быть 200 кГц (влево-вправо от несущей частоты по 100 кГц), в пределах которой помещается две спектральные линии частоты следования F_c (рис. 3.4). Длительность импульса τ=1/100·10^-3=10 мкс. Скорость передачи информации составит 1/10 мкс = 100 000 импульсов в секунду или 100 кбит/с.

Для ЧМн сигнала (рис. 3.6). В пределах ширины спектра 200 кГц должно поместиться четыре спектральные линии частоты следования F_c и частотный сдвиг Δf. Примем значение Δf равным восьми спектральным линиям частоты следования F_c. Тогда, в соответствии с (3.3):

ΔF_ЧМ = 2k · F_c + 2· Δf_m = 2·2· F_c +2·8· F_c =200 кГц;

F_c·(4 + 16) = 200; F_c = 10 кГц.

В пределах ширины спектра на уровне 1/τ помещается две спектральные линии частоты следования F_c.

Длительность импульса τ=1/2F_c=50 мкс. Скорость передачи информации составит 1/50 мкс = 20 000 импульсов в секунду или 20 кбит/с.

Для ФМн сигнала (рис.3.8) скорость передачи информации такая же, как и для АМн сигнала, т.е. 100 кбит/с.

Если применить 4-х позиционную частотную или фазовую манипуляции, то скорость передачи информации составит, соответственно, для ЧМн – 40 кбит/с и ФМн (QPSK) – 200 кбит/с.