1.3 Электрические сигналы: классификация, параметры

Электрические сигналы различают на непрерывные и дискретные сигналы. Непрерывный электрический сигнал часто называют аналоговым.

Аналоговые сигналы, например речевые, описываются непрерывной функцией времени (рис. 1.9).

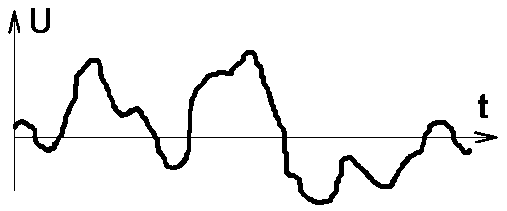
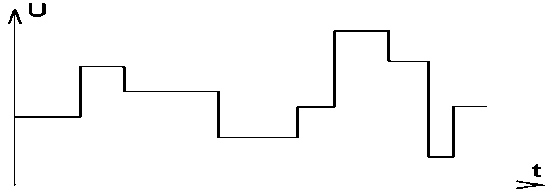
Рис.1.9 Временная диаграмма Рис.1.10 Временная диаграмма

аналогового сигнала дискретного сигнала

Дискретные электрические сигналы характеризуются конечным числом значений информационного параметра. Например, электрический сигнал, изображенный на рис. 1.10, имеет 9 значений амплитуды. Подобной формы сигнал может быть на выходе видикона в телевидении или же, ФЭУ в факсимильной связи.

В системе передачи данных, информационный параметр может принимать одно из двух значений: «1» или «0»; где значению «1» соответствует высокий уровень напряжения или тока, а значению «0» – низкий. Дискретные электрические сигналы такого вида называются цифровыми (рис. 1.11).

Сигналы делятся также на периодические, значения которых повторяются через определённые промежутки времени, и непериодические.

Простейший периодический сигнал имеет форму гармонического колебания (рис. 1.12), математическое выражение которого, имеет следующий вид:

, (1.1)

где: u - мгновенное или текущее значение напряжения сигнала;

U_m - амплитудное значение напряжения (амплитуда);

ω - угловая (круговая) частота сигнала. Период T, угловая частота ω и частота f связаны зависимостью: ω = 2πf, f = 1/T;

- начальная фаза. Начальная фаза сигнала на рис. 1.12 равна 180°.

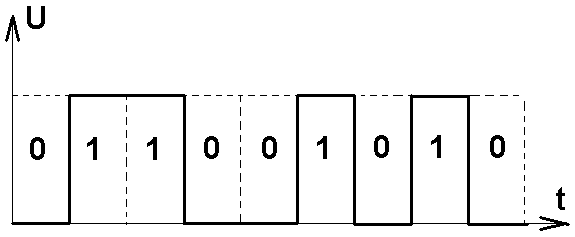
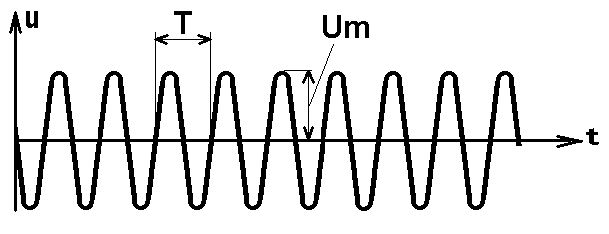
Рис. 1.11 Временная диаграмма цифрового Рис. 1.12 Временная диаграмма

сигнала гармонического сигнала

Для гармонических сигналов, период T соответствует одному колебанию, т.е. в течение периода текущая фаза сигнала изменяется от 0º до 360º. Величина, обратная периоду называется частотой. Частота f характеризует количество колебаний в единицу времени. Например, частота f = 50 Гц означает, что в течение одной секунды совершается 50 колебаний. Применяется также другая размерность: килогерц - 1 кГц = 10³ Гц, мегагерц - 1 МГц = 10⁶ Гц, гигагерц -1 ГГц = 10⁹ Гц.

1.3.1 Понятие спектра сигнала

Как известно, обычный видимый свет является сложным, состоящим из простейших цветов (цвета радуги), каждый из которых, имеет свою частоту электромагнитных колебаний. Эти цвета образуют спектр света.

В системах электросвязи также приходится иметь дело со сложными сигналами, которые, в общем случае, состоят из простейших гармонических колебаний разных частот.

Например, на рис. 1.13 представлен результат алгебраического сложения трех гармонических сигналов u₁, u₂ и u₃, периоды колебания которых, соответственно Т₁, Т₂ и Т₃ [11].

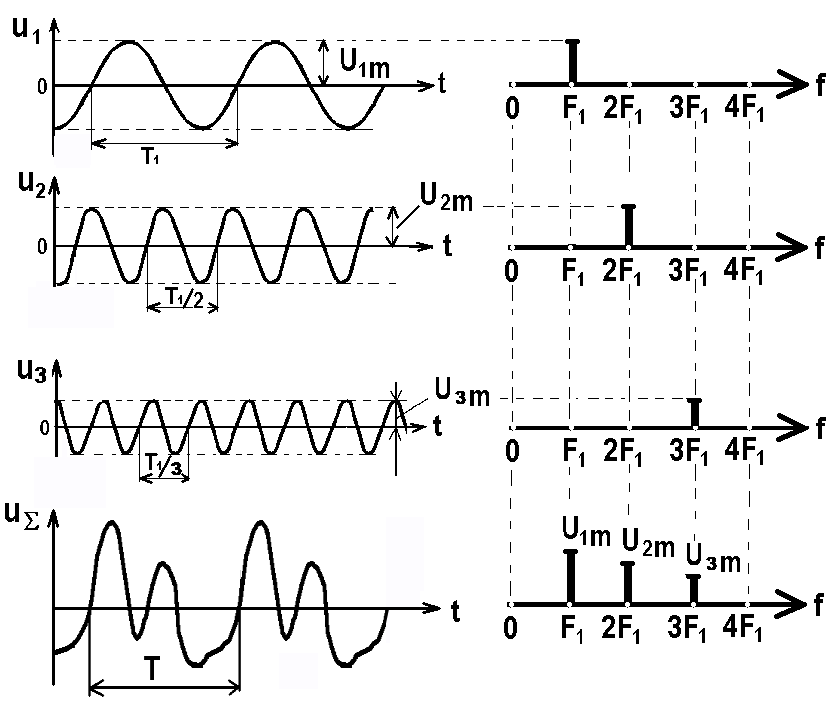
а) б)

Рис. 1.13 Графическое представление результата сложения трех периодических сигналов: а) временные диаграммы; б) амплитудно-частотный спектр

Причем, частота (F = 1/Т) сигналов u₂ и u₃ является кратной F₁, т.е. F₂=2F₁ и F₃=3F₁. Справа от временных диаграмм (рис. 1.13,б), сигналы представлены в виде амплитудно-частотного спектра. На этих диаграммах, ось абсцисс образует шкалу ча­стот f = nF₁, где n-целое число, а на оси ординат откладываются отрезки, длина кото­рых пропорциональна амплитудным значениям U_nm сигналов (без учета начальных фаз гармоник).

Как видим (рис. 1.13,а), форма суммарного сложного сигнала u_Ʃ, повторяется через временной промежуток Т. Следовательно, этот сигнал является периодическим, период колебания которого, равен периоду колебания сигнала u₁, т.е. Т = Т₁.

Таким образом, если результатом сложения нескольких гармонических сигналов, является периодический сложный сигнал, то, очевидно, и любой сложный периодический сигнал можно разложить на простейшие гармонические составляющие.

Так в соответствии с [11], любой сложный периодический сигнал можно представить в виде совокупности простейших гармонических сигналов, значения амплитуд (U_nm), частот (ω_n) и начальных фаз (φ_n) которых, можно найти посредством разложения в ряд Фурье:

, (1.2)

где n = 1,2,3… - целое число, а Ω = 2πF, F=1/Т.

Примечание. В дальнейшем, частоту высокочастотного колебания будем обозначать буквой f, а низкочастотного – F.

Гармонические сигналы, частота которых F₁=F, F₂=2F, F₃=3F и т.д. именуются соответственно: первая, вторая, третья гармоники.

Таким образом, спектр сигнала – это совокупность гармоник (гармонических составляющих) с конкретными значениями частот и амплитуд, образующих в сумме сложный электрический сигнал. Спектр может быть представлен в виде графического изображения, т.е. изображения амплитуд гармоник на оси частот (рис. 1.13, б).

Характерно, что спектр периодических сигналов не сплошной, а линейчатый, т. е. между соседними линиями спектра имеются «просветы» шириной в частоту следования сигнала .

Более сложный сигнал, например, приведенный на рис. 1.9 (круче изгибы), характеризуется большим количеством составляющих от F_н до F_в, где F_н и F_в соответственно нижняя и верхняя составляющие спектра сигнала.

Интервал (диапазон) частот F_в - F_н = ΔF называется шириной спектра сигнала. Ширина спектра сигнала – это интервал (диапазон) частот, в пределах которого сосредоточена основная часть энергии сигнала.

Так, спектр звукового сигнала (музыка и пение, включающие в себя и спектр речи) имеет общую ширину 20...20 000 Гц и зависит от класса вещания:

1-ый класс – 50...10 000 Гц; высший класс – 30...15 000 Гц и т.д.

Частотный спектр речи лежит в пределах: от 50 Гц до 10 000 Гц. Частота основного тона речи находится в пределах от 50...80 Гц (самый низкий мужской) до 200...250 Гц (самый высокий женский или детский).

Звуки речи различных людей отличаются количеством формант (спектральных областей резонанса при произношении звуков речи) и их мощностью. Из рис. 1.14 [3] видно, что форманта буквы «А» находится в спектре частот, близких к частоте 950 Гц, а форманта буквы «Е» - к частоте 690 Гц. Установлено экспериментально, что все остальные форманты гласных и согласных звуков, из которых складывается речь, не выходят за пределы спектра 300...3400 Гц.

Рис. 1.14 Спектральный состав речевого сигнала

В соответствии с МСЭ-Т (Международной организацией по электросвязи), качество речи можно считать удовлетворительным, если передаются шесть формант. Спектр частот, при этом, может быть ограничен диапазоном 300-3400 Гц [4]. Такой сигнал называется сигналом тональной частоты (ТЧ).