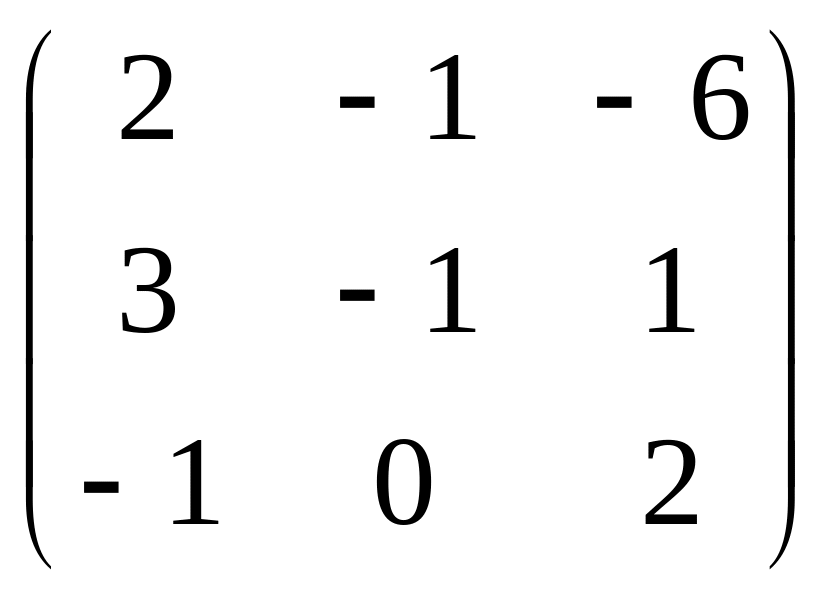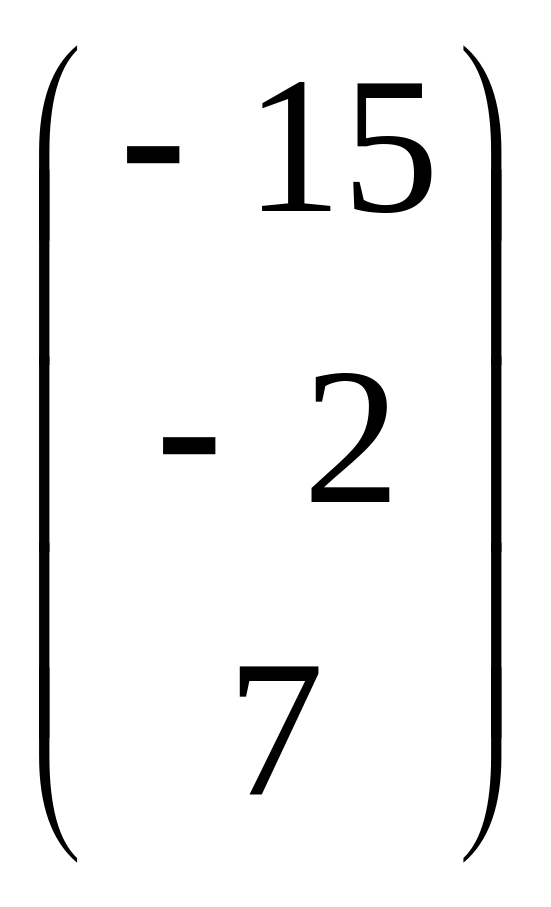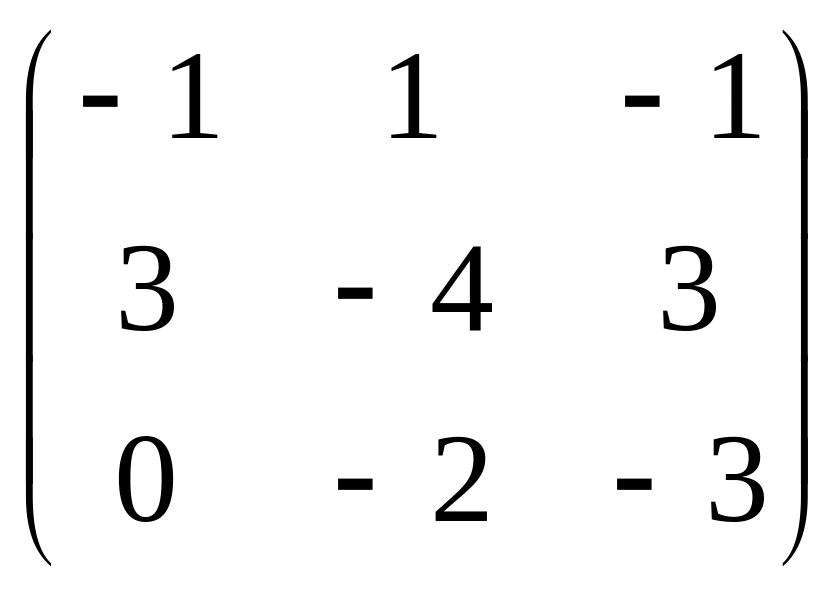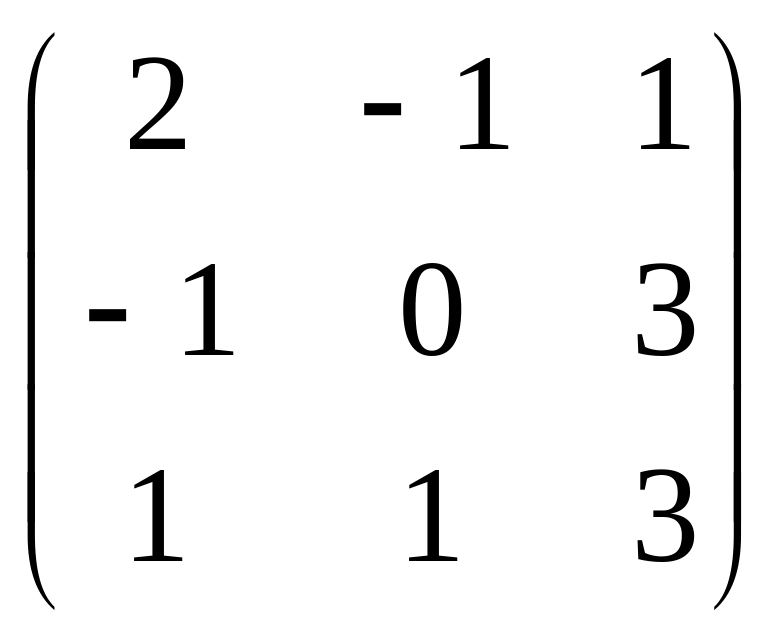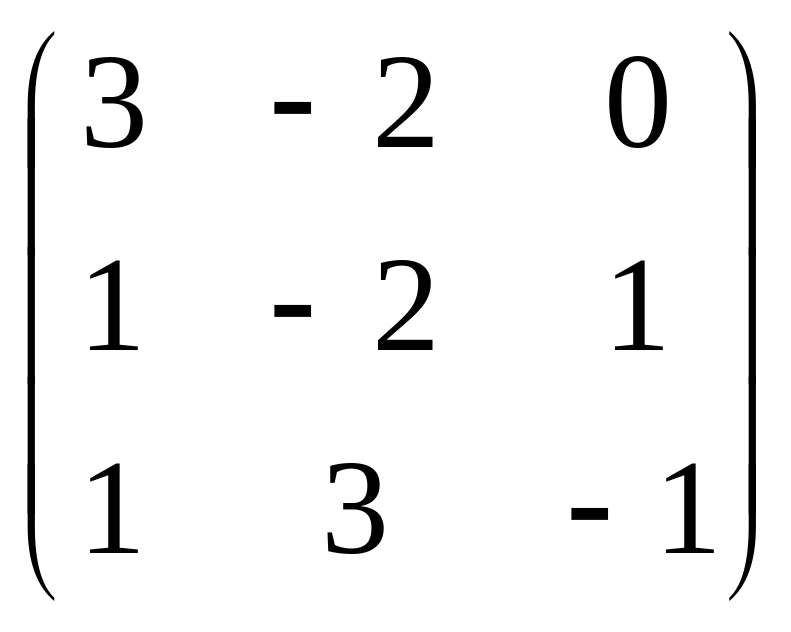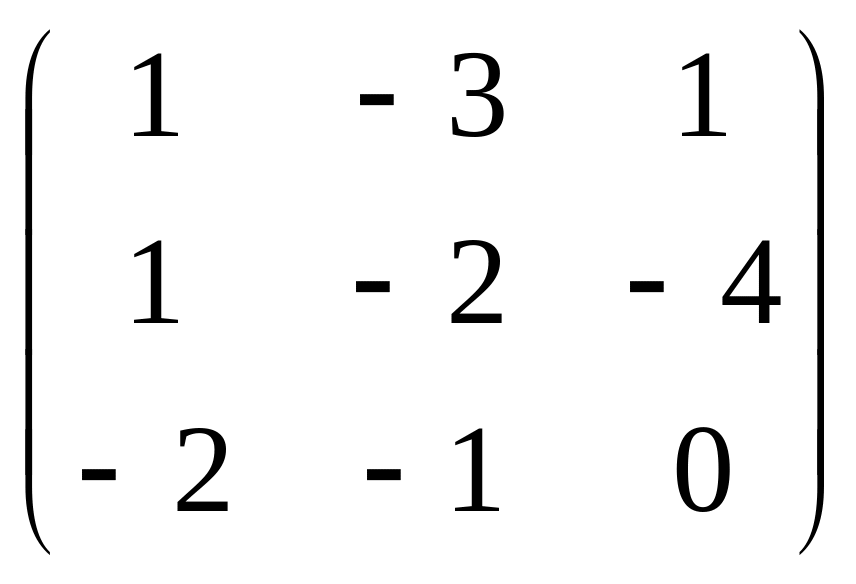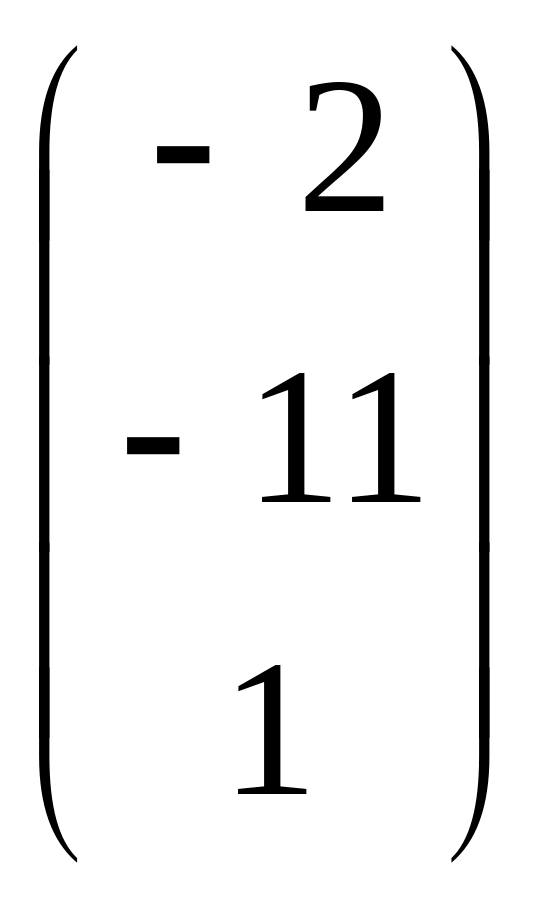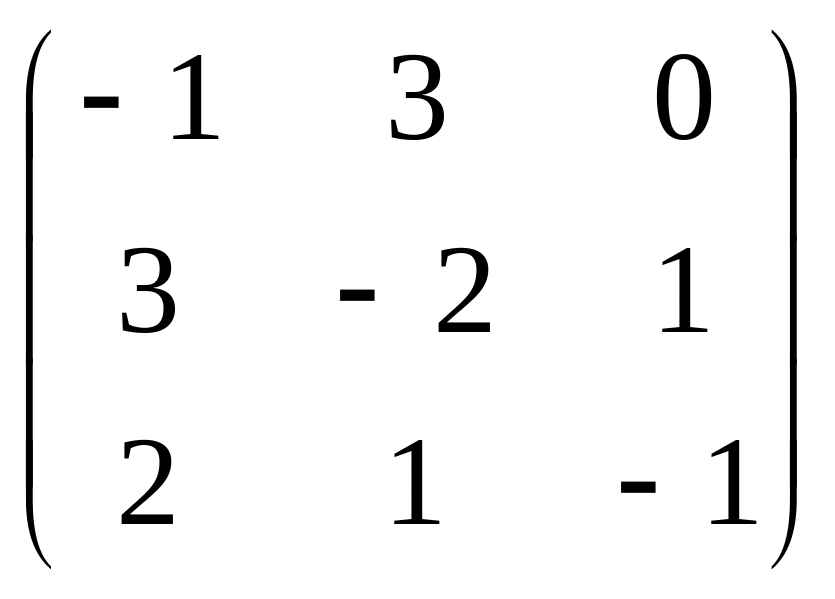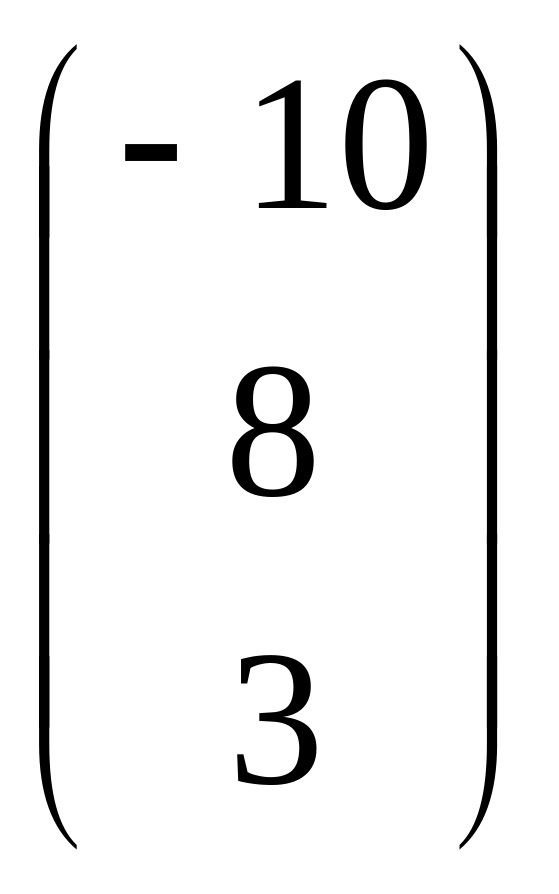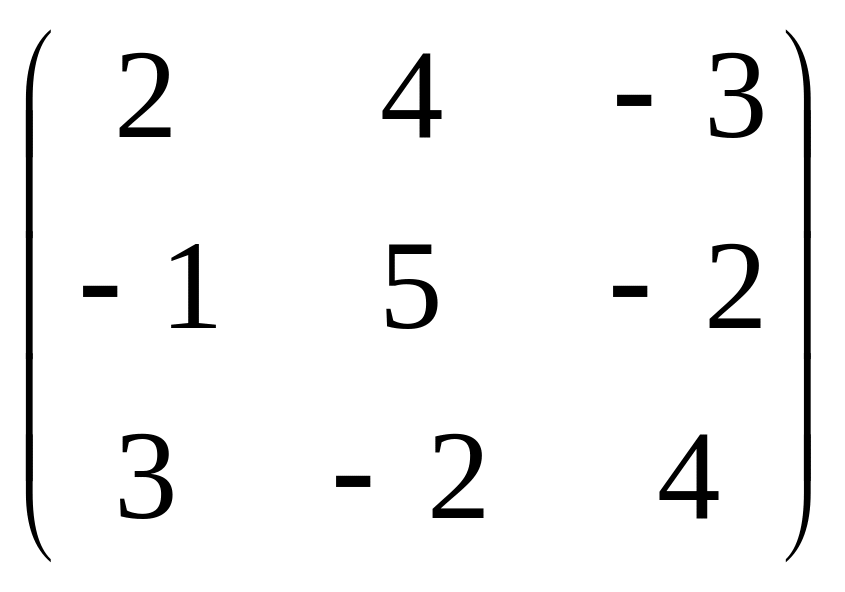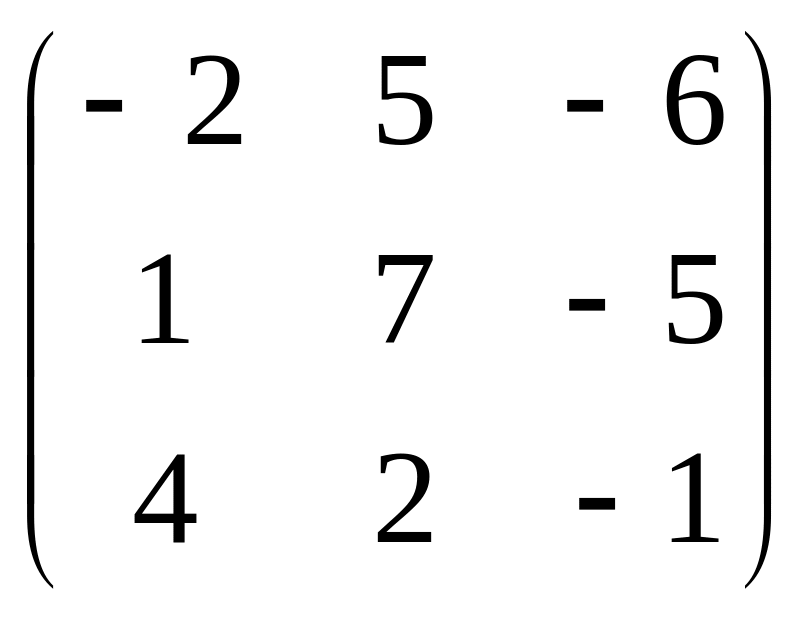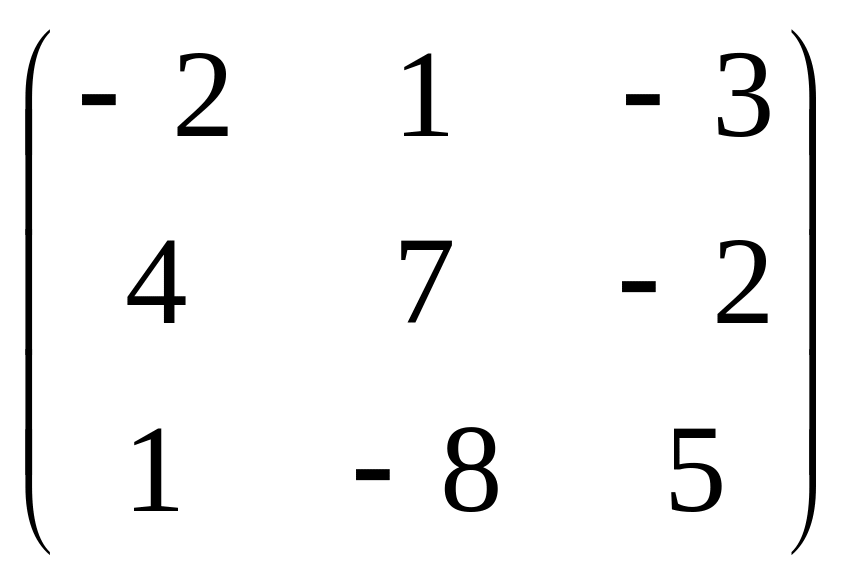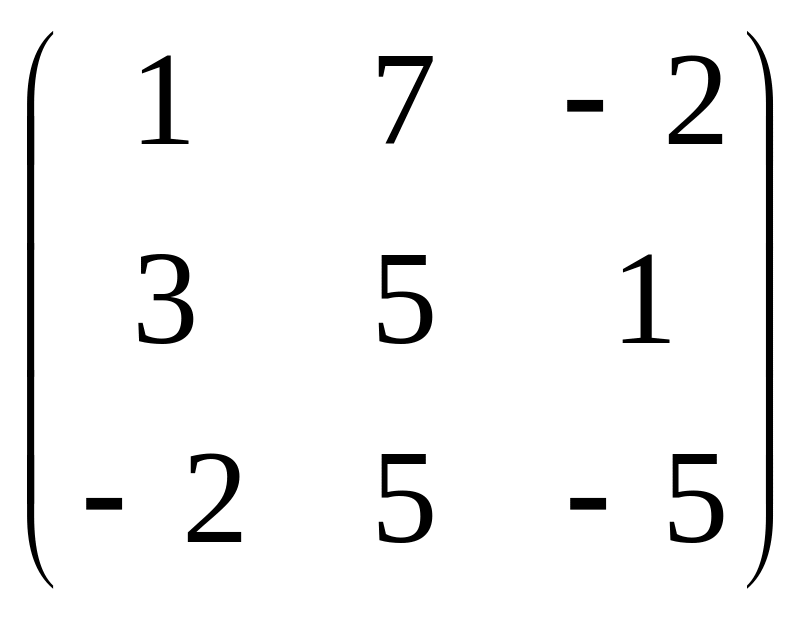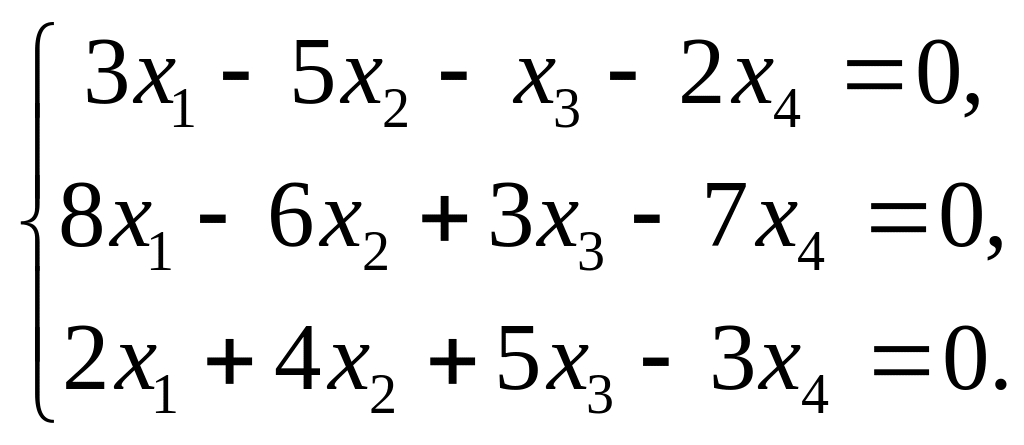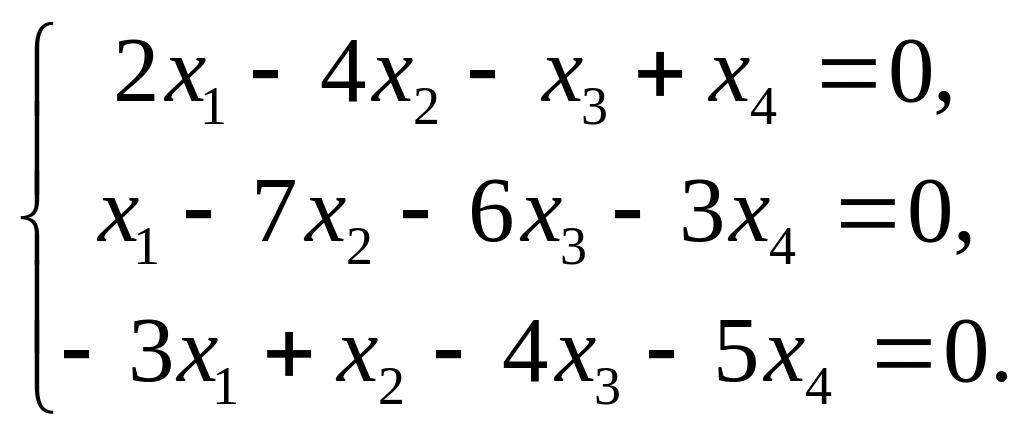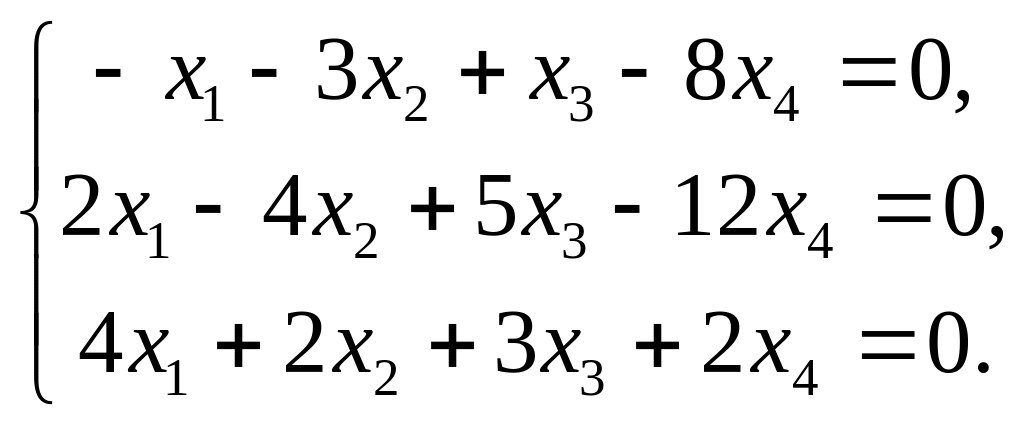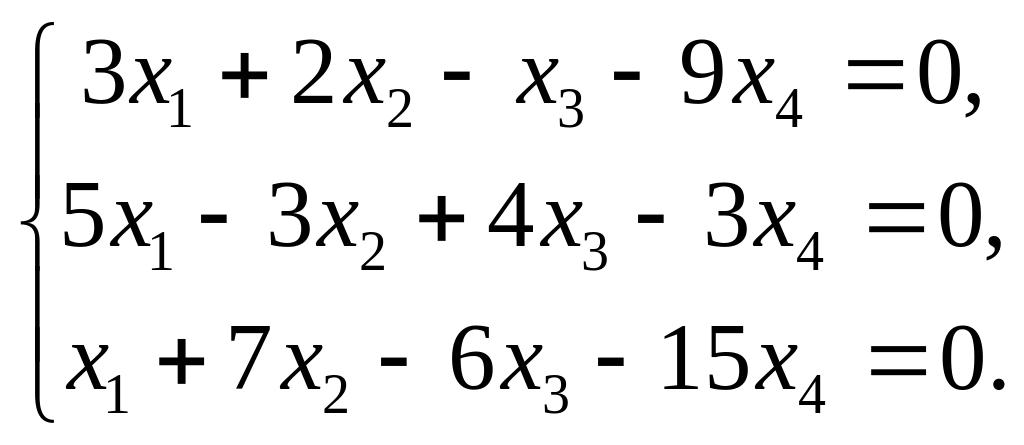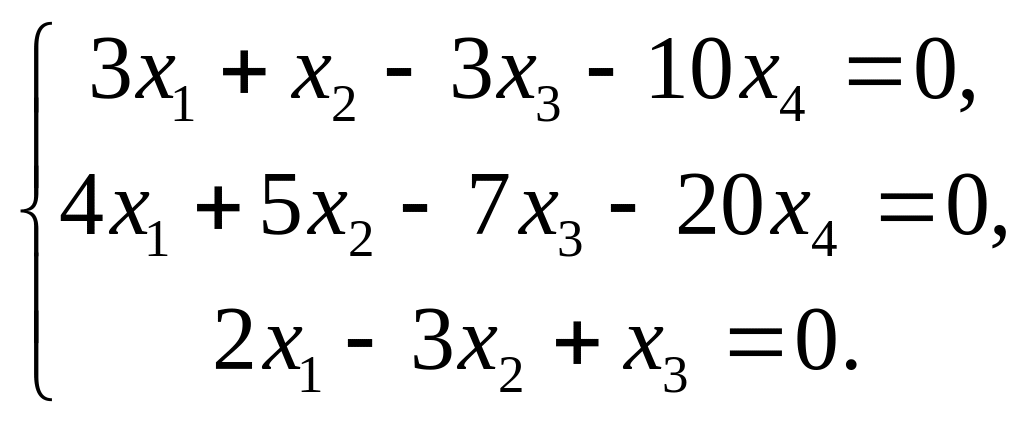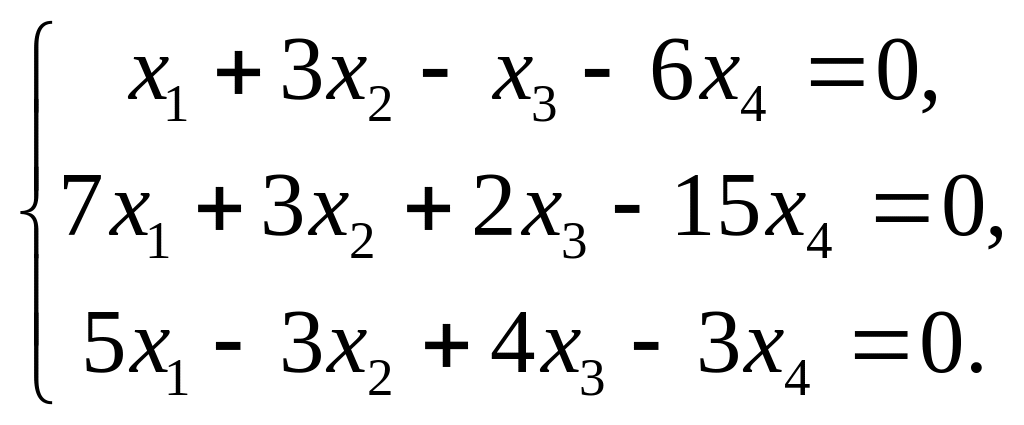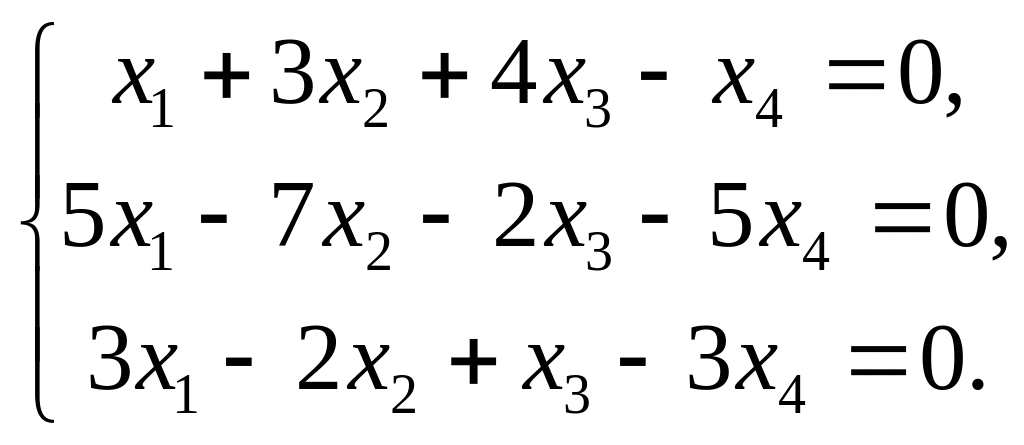Варианты контрольных работ Задачи для контрольной работы Часть1 Задание 1
Даны матрицы:
А
=
;
В =
;
С =
.
Требуется:
вычислить матрицу b1А + b2С + b3Ст;
проверить, выполняется ли равенство А∙С = С∙А;
вычислить определители ∆(А), ∆(С), ∆(А∙С) и проверить равенство ∆(А∙С)= ∆(А) ∙ ∆(С);
решить систему уравнений А∙х = В с помощью формул Крамера;
решить систему уравнений А∙х = В средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
№ варианта |
A |
B |
C |
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
Задание 2
Дана однородная система трех линейных уравнений с четырьмя неизвестными.
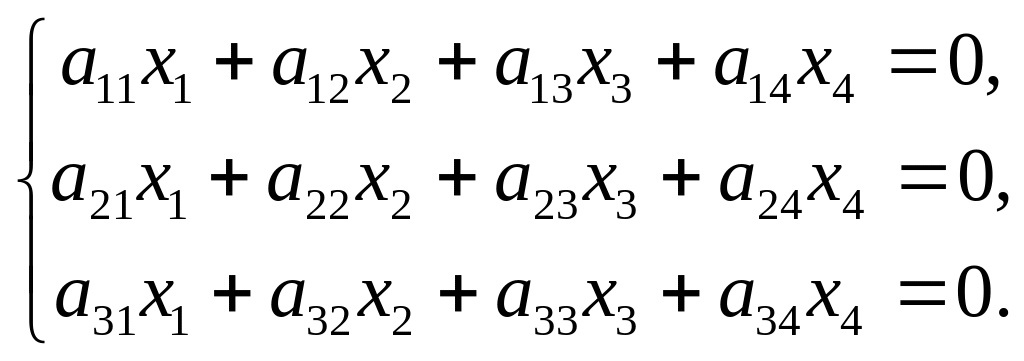
Записать систему в матричной форме и найти множество решений системы.
№ варианта |
система |
№ варианта |
система |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
Задание 3
Доказать,
что система
образует базис в L.
Найти матрицу перехода B
от базиса E
к базису Е'
и координаты вектора
относительно
базиса Е',
если:
№ варианта |
|
|
|
|
|
|
(0; 1; 2) |
(1; 2; 2) |
(-1; 2; 2) |
(1; -1; 3) |
|
|
(1; 1; -1) |
(2; 1; 0) |
(0; 1; 0) |
(-1; 2; 1) |
|
|
(-2; 1; 1) |
(-2; 2; 2) |
(-2; 0; 2) |
(0; 3; -1) |
|
|
(1; -3; 2) |
(0; -4; 2) |
(2; -4; 2) |
(-1; 0; 4) |
|
|
(1; 0; 2) |
(0; 0; 1) |
(2; 0; 1) |
(2; -3; 1) |
|
|
(1; -1; 1) |
(1; -2; 0) |
(1; 0; 0) |
(-2; 3; 3) |
|
|
(1; -2; 1) |
(2; -1; 1) |
(2; -3; 1) |
(3; 1; -3) |
|
|
(1; 2; -3) |
(2; 2; -2) |
(2; 2; -4) |
(-2; -2; -1) |
|
|
(2; 1; 0) |
(2; 2; 1) |
(2; 2; -1) |
(-3; 0; 2) |
|
|
(-1; 1; 1) |
(-2; 0; 1) |
(-2; 2; 1) |
(2; 2; -4) |
