Экстремум в экономике.

Математические методы широко используются в таких вопросах, как планирование народного хозяйства, организация управления, планирование военных операций и т.д. Задачи управления и планирования обычно сводятся к выбору некоторой системы числовых параметров или функции, обеспечивающих наиболее эффективное достижение поставленной цели (оптимальный план) с учётом ограниченности возможных ресурсов. Слово оптимальный происходит от латинского слова optimum – наилучший.

Для оценки эффективности плана вводится так называемая целевая функция (показатель качества плана), выраженная через характеристики плана и принимающая экстремальные значения (наименьшее или наибольшее значения) для оптимального плана.

Задачи оптимизации бывают линейные и нелинейные.

Нелинейные задачи оптимизации решают методами классического анализа. В научных исследованиях и производственных испытаниях результаты опытов чаще всего изображаются в виде таблиц и графиков. Полученные опытные данные обычно подвергают математической обработке, выражая их с помощью формулы с точностью, не превышающей определённой погрешности. Полученная при этом функция имеет ограничения, отражающие условия производства и особенности динамики процессов. В интересах производства важно знать такие значения независимой переменой, при которых производственная функция принимает наибольшее или наименьшее значение.

Задача.

Решёткой длиной 120 м. нужно огородить прилегающую к дому прямоугольную площадку наибольшей площади. Определить размеры прямоугольной площадки.

Решение:

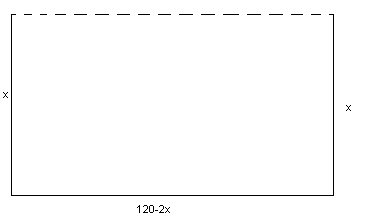Обозначим через одну из сторон прямоугольной площадки. Тогда другая сторона будет равна

.

А площадь прямоугольной площадки будет равна

.

Тогда

;

=> =>

=>

- точка максимума.

Следовательно, размеры площади должны быть 30 Х 60 м., тогда площадь прилегающего участка будет наибольшей, равной 1800 м².

Для большого числа практически важных задач целевая функция выражается линейно через характеристики плана, а допустимые значения параметров также подчинены линейным равенствам или неравенствам.

Нахождение при данных условиях абсолютного экстремума целевой функции решается методом линейного программирования.

Математически задача линейного программирования формулируется так: требуется найти абсолютный экстремум (наибольшее или наименьшее значение в зависимости от смысла задачи) линейной целевой функции

(1)

при условии, что на переменные , , ∙∙∙ , наложены ограничения в виде линейных равенств или неравенств:

, , ∙∙∙ , (2)

(3) .

Опр. Максимальная совокупность G значений x 1, x2, ∙∙∙ , xn , удовлетворяющая всем неравенствам (2) и (3) называется областью допустимых значений задачи линейного программирования (Допустимой областью).

Допустимая область G является областью определения функции S.

Допустимая область задачи линейного программирования представляет собой выпуклый многогранник.

Опр. Множество значений , , ∙∙∙ , из допустимой области G, при которых целевая функция (1) принимает, по смыслу задачи, или наименьшее или наибольшее значение, называется решением задачи линейного программирования (оптимальным планом). В случае существования хотя бы одного решения задача линейного программирования называется разрешимой.

Заметим, что целевая функция достигает своего абсолютного экстремума или в критической точке, или на границе допустимой области G, т.е. в вершинах многогранника G (иногда во всех точках грани многогранника).

Таким образом, решение задачи линейного программирования сводится к нахождению конечного числа значений целевой функции и сравнению их между собой.

Задача. Предприятие имеет возможность приобрести не более 20 трёхтонных и не более 18 пятитонных автомашин. Отпускная цена трёхтонного грузовика 400 000 рублей, пятитонного 500 000 рублей. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъёмность была максимальной, если для приобретения выделено 15 000 000 рублей.

Задачу можно решить графическим и аналитическим способами.

Решение: Пусть приобретено трёхтонных и пятитонных автомобилей. Из условия задачи имеем:

(*)

Суммарная грузоподъёмность приобретённых грузовиков равна:

(**)

Задача состоит в нахождении такого решения системы, при котором линейная форма (целевая функция) принимает наибольшее значение.