Тема 3. Применение производной.

3.1. Применение производной к вычислению пределов.

Кроме элементарных способов, весьма эффективным средством для нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции, является правило Лопиталя.

Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если он существует или равен бесконечности.

Итак, если имеются неопределенности вида или , то

. (1)

Обращаем внимание, что в правой части формулы (1) берется отношение производных, а не производная отношения.

Пример. Найти: а) б) в)

Решение. а) Имеем неопределенность вида . Применяя правило Лопиталя, получим:

б)

Неопределенность вида по-прежнему сохраняется. Применим правило Лопиталя еще раз:

в) Имеем неопределенность вида . Переписываем данное выражение в виде

получим неопределенность вида . Применяя правило Лопиталя, получим

.

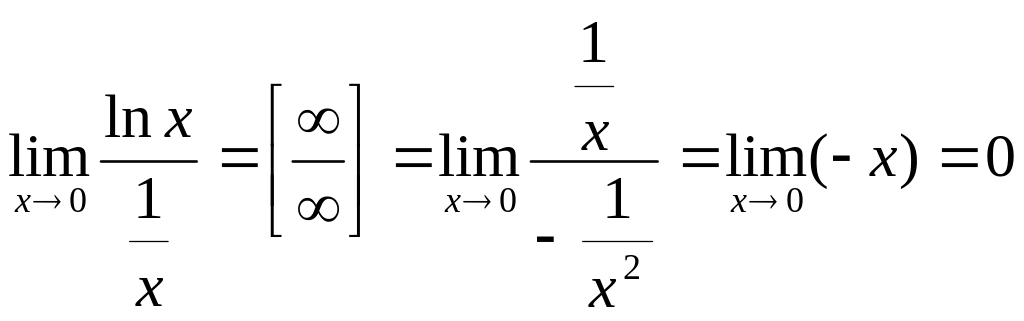3.2. Применение производной к исследованию функций.

Возрастание и убывание функций.

При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т.е. что каждое следующее ее значение больше предыдущего.

Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.

Некоторые функции во всей своей области определения изменяются монотонно – только возрастают или только убывают (например ).

Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают (например, sin x, cos x).

Возрастание и убывание функции характеризуется значением ее производной : если в некотором интервале >0, то функция возрастает, а если <0, то функция убывает в этом интервале.

Экстремум функции.

Значение функции в точке х_о называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа отх_о.

Функция может иметь экстремум (максимум или минимум) только в тех точках, которые лежат внутри области определения функции и где ее производная равна нулю или не существует. Такие точки называются критическими.

В соответствующих точках графика функции касательная параллельна оси абсцисс , или оси ординат или нет определенной касательной (например, как в угловой точке).

Точками экстремума являются все точки, где функция меняет свое поведение и непрерывна.

Точки, при переходе через которые аргумента х возрастание функции сменяется на убывание, являются точками максимума, а точки, при переходе через которые аргумента х убывание функции сменяется на возрастание, являются точками минимума.

Поскольку поведение функции характеризуется знаком ее производной, то функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна.

Отсюда вытекает следующее правило исследования функции на экстремум.

Чтобы найти точки экстремума функции , в которых она непрерывна, нужно:

1. Найти производную и критические точки, в которых =0 или не существует, а сама функция непрерывна, и которые лежат внутри области определения функции.

2а. Определить знак слева и справа от каждой критической точки.

Если при переходе аргумента х через критическую точку х_о:

1) меняет знак с + на -, то х_о есть точка максимума;

2) меняет знак с - на +, то х_о есть точка минимума;

3) не меняет знака, то в точке х_о нет экстремума.

Иногда проще исследовать критические точки, где , по знаку второй производной, - вместо правила 2а можно пользоваться следующим правилом:

2б. Найти вторую производную и определить ее знак в каждой критической точке.

Если в критической точке х_о, где :

1) >0, то х_о есть точка максимума;

2) <0, то х_о есть точка минимума;

3) =0, то вопрос о наличии экстремума в точке х_о остается открытым. Такую критическую точку, как и всякую другую, можно исследовать по правилу 2а.

Далее следует найти экстремумы функции, т.е. вычислить значения функции в найденных точках экстремума.

Выпуклость функции. Точки перегиба.

Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.

Точкой перегиба называется точка на кривой, где меняется направление ее выпуклости.

Направление выпуклости кривой характеризуется знаком второй производной : если в некотором интервале >0, то кривая выпукла вниз, а если <0, то кривая выпукла вверх в этом интервале.

Абсциссы точек перегиба кривой , или графика функции f(x), являются точками экстремума производной . Поэтому их можно найти по следующему правилу:

1. Найти и точки х, в которых =0 или не существует, а кривая непрерывна и которые лежат внутри области ее расположения.

2. Определить знак слева и справа от каждой из этих точек. Исследуемая точка х будет абсциссой точки перегиба, если по разные стороны от нее имеет разные знаки.

Интервалы, где кривая выпукла вверх и где она выпукла вниз, определяются из условия, что их границами могут быть только абсциссы точек перегиба, точки разрыва и граничные точки области расположения кривой.

Асимптоты.

Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.

Для нахождения асимптот пользуются следующими положениями:

а) если при х=а кривая имеет бесконечный разрыв, т.е. если при , то прямая х=а является вертикальной асимптотой;

б) если при существует конечный предел функции , т.е. , то прямая y=b горизонтальная асимптота графика функции ;

3) если существуют конечные пределы и , то прямая у = kx + b является наклонной асимптотой графика функции .

Общая схема исследования функций и построения их графиков.

При исследовании функций и построении их графиков рекомендуется использовать следующую схему:

1. Найти область определения функции.

2. Исследуем функцию на непрерывность.

3. Установим, является ли заданная функция четной, нечетной.

4. Найдем интервалы возрастания и убывания функции и точки экстремума.

5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

6. Найдем асимптоты кривой.

Заметим, что исследование функции проводится одновременно с построением ее графика.

Задача. Исследовать функцию и построить ее график.

Решение. Реализуем указанную схему.

1. Функция определена при всех значениях аргумента х, кроме х = 1.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервале (-∞; 1) и (1; +∞).

В точке х = 1 функция терпит разрыв второго рода.

3. Для установления четности или нечетности функции проверим выполнимость равенств 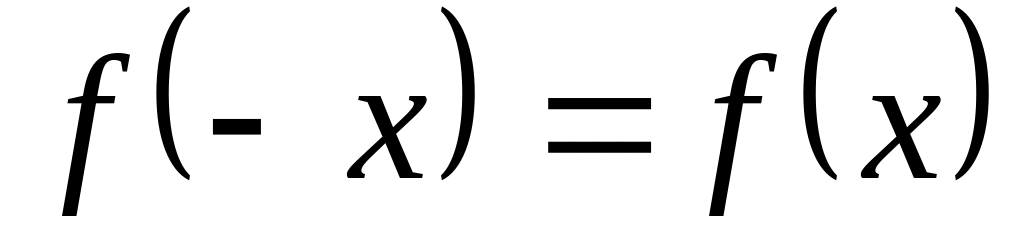(тогда - четная функция) или ( для нечетной функции) для любых х и –х из области определения функции: 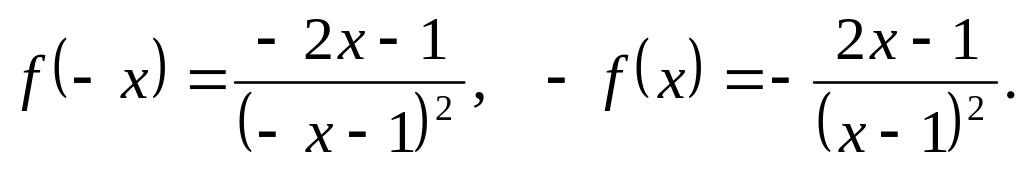Следовательно, 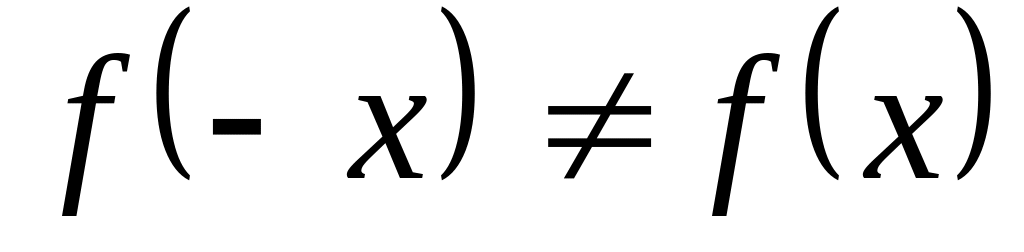и , то есть данная функция не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем ее первую производную:

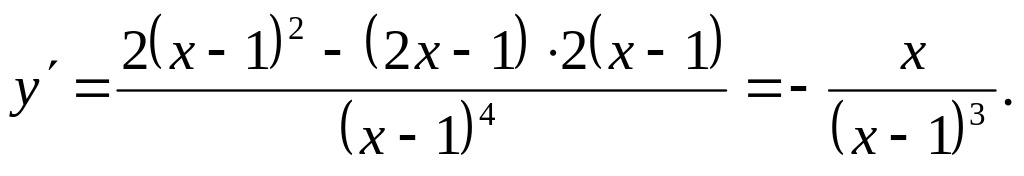
при х = 0 и - не существует при х = 1. Тем самым имеем две критические точки: х₁ = 0 и х₂ = 1. Но точка х₂ = 1 не принадлежит области определения функции, экстремума в ней быть не может.

Разобьем числовую ось на 3 интервала:

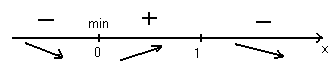
В первом и третьем интервалах функция отрицательна, следовательно, здесь функция убывает; во втором интервале – положительна, и данная функция возрастает. При переходе через точку х = 0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: . Значит, А(0; -1) – точка минимума.

5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную: 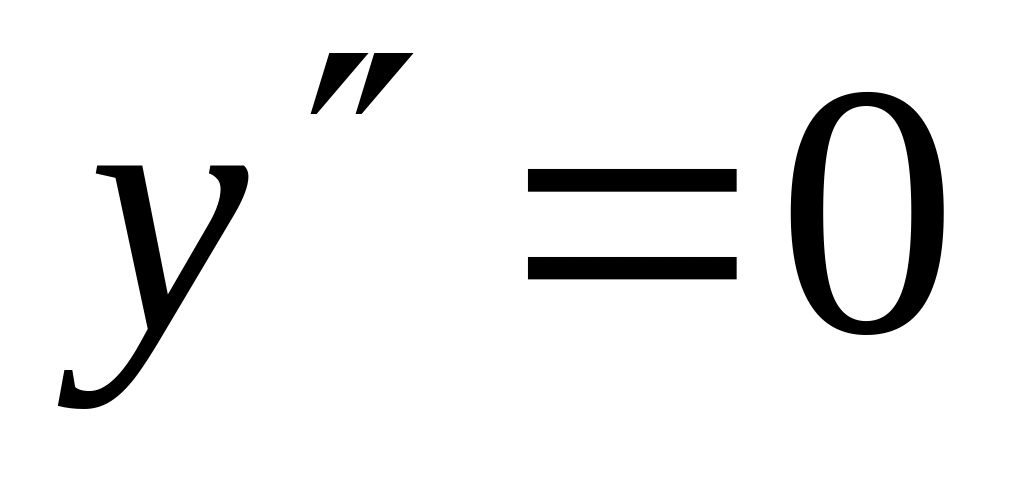при 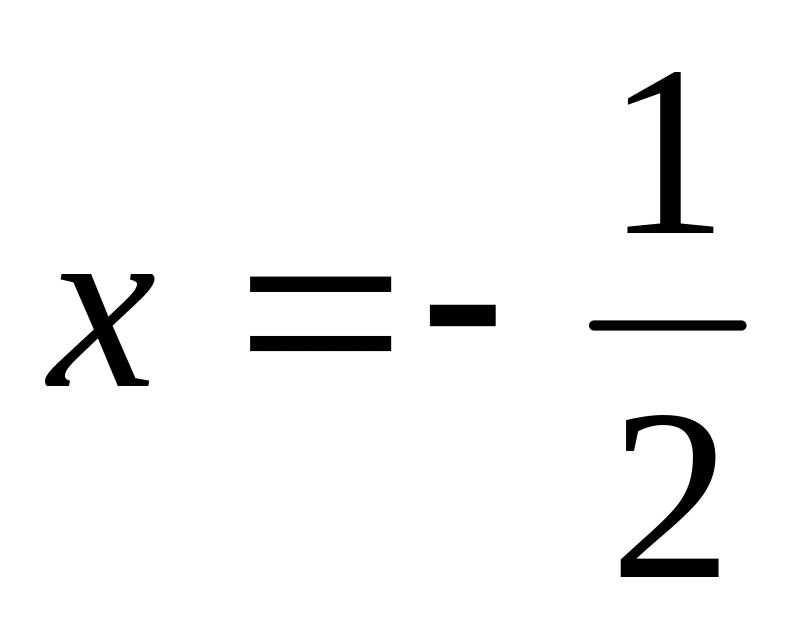и - не существует при х = 1. Разобьем числовую ось на три интервала: На первом интервале вторая производная отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах > 0, тем самым график является вогнутым. При переходе через точку , меняет свой знак, поэтому - абсцисса точки перегиба. Следовательно, В точка перегиба графика функции.

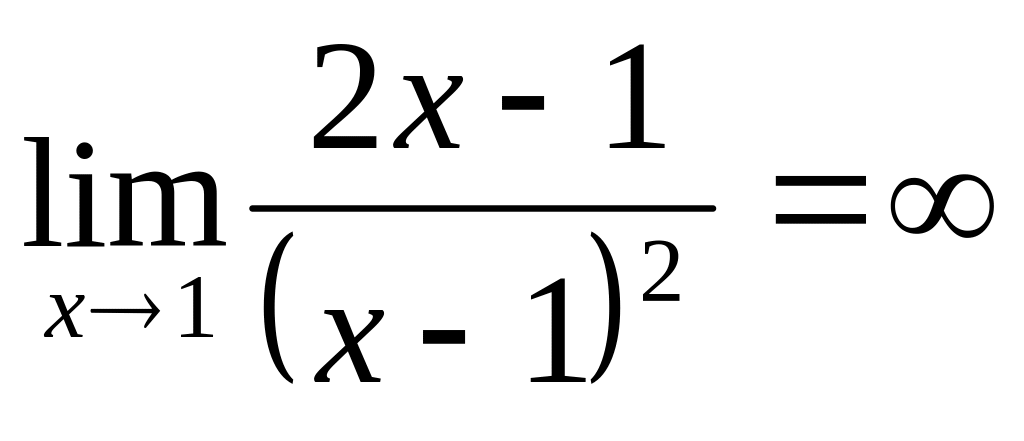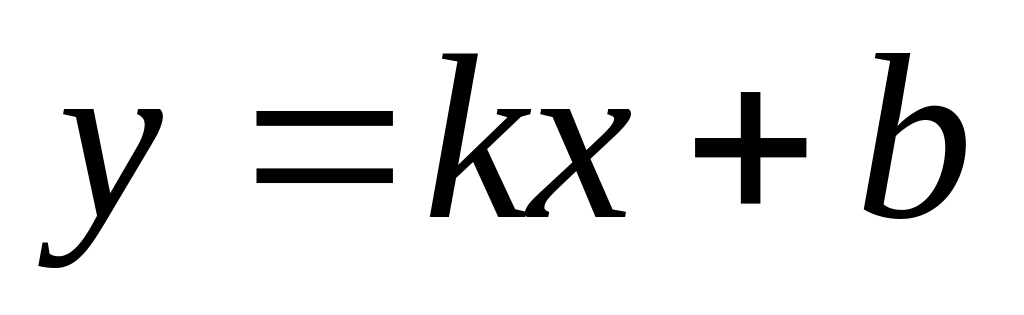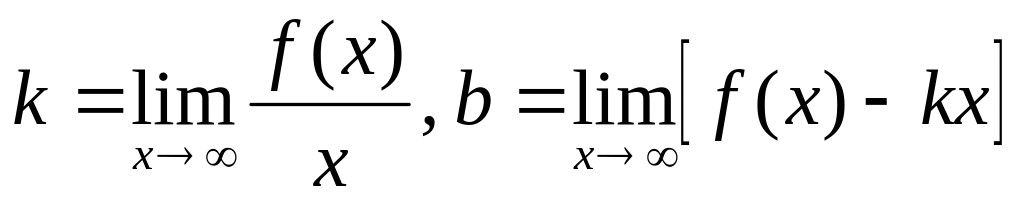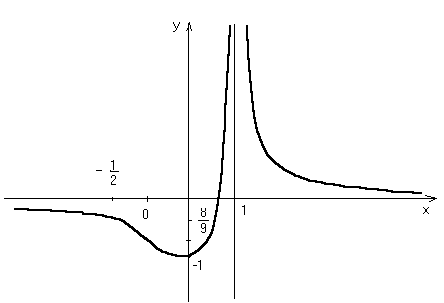
6. x = 1 – точка разрыва функции, причем . Поэтому прямая х = 1 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты воспользуемся формулами: . Тогда , . Значит, прямая у = 0 есть горизонтальная асимптота графика исследуемой функции, представленного на рисунке.