
- •Элементы теории корреляции
- •1. Функциональная, статистическая и корреляционная зависимости
- •2.Условное средние
- •3. Выборочные уравнения регрессии
- •5. Корреляционная таблица
- •6. Выборочный коэффициент корреляции
- •7.Виды корреляции
- •7.1Линейная корреляция
- •7.2 Криволинейная корреляция
- •7.3 Ранговая корреляция
7.Виды корреляции
7.1Линейная корреляция
Если обе линии регрессии У на X и X на К — прямые, то корреляцию называют линейной.
Выборочное уравнение прямой линии регрессии У на X имеет вид
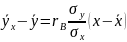
где
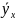 — условная средняя;
— условная средняя;
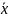 и
и
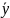 — выборочные средние
признаков X и У:
— выборочные средние
признаков X и У:
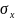 и
и
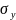 —
выборочные средние квадратические
отклонения;
—
выборочные средние квадратические
отклонения;
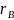 —выборочный
коэффициент корреляции, причем
—выборочный
коэффициент корреляции, причем
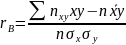
Выборочное
уравнение прямой линии регрессии
X на Y имеет
вид
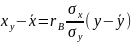
Если данные наблюдений над признаками X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целе-сообразно перейти к условным вариантам:
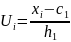 и
и
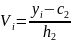
где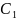 —«ложный
нуль» вариант X (новое начало отсчета);
в качестве ложного нуля выгодно принять
варианту. которая расположена примерно
в середине вариационного ряда (условимся
принимать в качестве ложного нуля
варианту, имеющую наибольшую частоту);
—«ложный
нуль» вариант X (новое начало отсчета);
в качестве ложного нуля выгодно принять
варианту. которая расположена примерно
в середине вариационного ряда (условимся
принимать в качестве ложного нуля
варианту, имеющую наибольшую частоту);
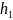 — шаг, т. е. разность между двумя соседними
вариантами Х;
— шаг, т. е. разность между двумя соседними
вариантами Х;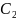 —
ложнsй
нуль вариант Y;
—
ложнsй
нуль вариант Y;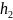 —
шаг вариант Y.
—
шаг вариант Y.
Пример №535
7.2 Криволинейная корреляция
Если график регрессии — кривая линия, то корреляцию называют криволинейной. В частности, в случае параболической корреляции второго порядка выборочное уравнение регрессии Y на X имеет вид
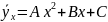
Неизвестные параметры А, В и С находят (например, методом Га-усса) из системы уравнений:
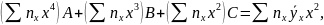
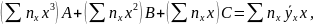
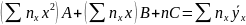
Аналогично находится выборочное уравнение регрессии X на Y:
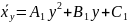
Пример №537
7.3 Ранговая корреляция
А. Выборочный коэффициент ранговой корреляции Спирмена.
Пусть выборка объема п содержит независимые объекты, которыеобладают двумя качественными признаками: А и В. Под качественным подразумевают признак, который невозможно измерить точно, но он позволяет сравнивать объекты между собой и, следовательно, расположить их в порядке убывания пли возрастания качества. Для определенности условимся располагать объекты» порядке ухудшения качества.
Расположим
сначала объекты в порядке ухудшении
качества по признаку А.
Припишем
объекту, стоящему на i-м
месте,
число — ранг
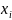 -,
равный порядковому номеру объекта:
-,
равный порядковому номеру объекта:
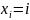 .
Затем расположим объекты в порядке
убывания качества по признаку В
и
при-пишем каждому из них ранг (порядковый
номер)
.
Затем расположим объекты в порядке
убывания качества по признаку В
и
при-пишем каждому из них ранг (порядковый
номер)
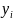 ,
причем
(для удобства сравнения рангов) индекс
i
при
у
по-прежнему равен порядковому номеру
объекта по признаку А.
,
причем
(для удобства сравнения рангов) индекс
i
при
у
по-прежнему равен порядковому номеру
объекта по признаку А.
В итоге получим две последовательности рангов:
по
признаку A
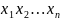
по
признаку B
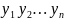
Выборочный коэффициент ранговой корреляции Спирмена нахо-дят по формуле
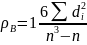
где
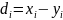 ,
n—объем
выборки.
,
n—объем
выборки.
Абсолютная
величина коэффициента ранговой корреляции
Спирмена не превышает единицы:
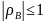
Пример №540
Б. Выборочный коэффициент ранговой корреляции Кендалла
Можно оценивать связь между двумя качественными признаками, используя коэффициент ранговой корреляции Кендалла. Пусть ранги объектов выборки объема n(здесь сохранены все обозначения п. А):
по признаку A
по признаку B
Допустим,
что справа от
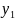 имеется
имеется
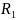 рангов,
больших
;
справа от
рангов,
больших
;
справа от
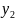 имеется
имеется
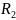 рангов,
больших
;справа
от
рангов,
больших
;справа
от
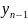 имеется Rn-i
рангов,
больших
имеется Rn-i
рангов,
больших
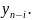 Введем
обозначение суммы рангов:
Введем
обозначение суммы рангов:
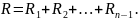
Выборочный коэффициент ранговой корреляции Кендалла нахо-дят по формуле:
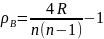
где
n
— объем выборки, R
—
сумма рангов
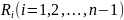
Абсолютная величина коэффициента ранговой корреляции Кен-далла не превышает единицы:
Пример №548
