9.2. Двоичные счетчики

Счетчики составляют важную группу схем последовательностного типа. Любая такая схема может служить счетчиком, лишь бы в определенных границах обеспечивалось однозначное соответствие между количеством введенных импульсов и состоянием выходной переменной. Поскольку каждая переменная способна принимать только два значения, n выходов дают 2ⁿ возможных комбинаций. Нередко используется только часть возможных комбинаций. Какому числу будет сопоставлена та или иная комбинация, безразлично. Однако в счетчиках целесообразно выбирать способ представления чисел, облегчающий обработку данных. В простейших схемах довольствуются чисто двоичным способом.

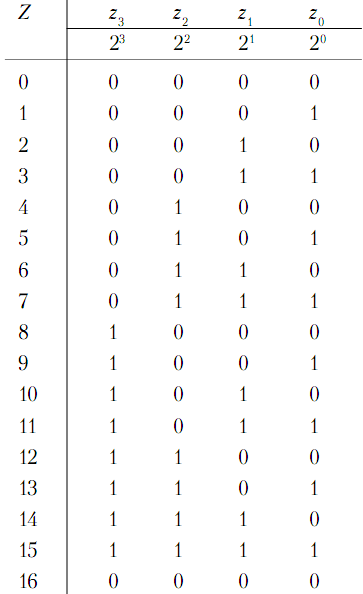
В табл. 9.6 показано, как число принятых импульсов Z соответствует значениям

переменной z_i в 4-разрядном двоичном счетчике. Просматривая таблицу сверху вниз, можно заметить две закономерности:

• смена значения выходной переменной z_i происходит тогда, когда переменная

ближайшего младшего разряда совершает переход от 1 к 0;

• выходная переменная меняется всякий раз, когда поступает новый импульс,

а все младшие переменные z_i–1…z₀ равны 1.

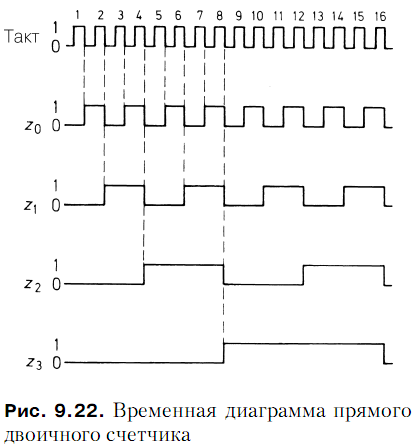
Это же видно и на временной диаграмме на рис. 9.22. Первая закономерность

приводит к реализации счетчиков, основанных на асинхронном методе, а вторая –

к реализации синхронного счетчика.

Иногда требуются счетчики, состояние которых уменьшается на единицу с каждым счетным импульсом. Особенности в работе такого счетчика, называемого вычитающим, также видны из табл. 9.6 при чтении снизу вверх.

Отсюда следует, что:

• в вычитающем счетчике выходная переменная z_i меняет свое значение тогда,

когда переменная ближайшего младшего разряда z_{i –1} совершает переход от 0 к 1;

• в вычитающем счетчике выходная переменная z_i меняется всякий раз, когда

поступает новый импульс, а все младшие переменные z_{i –1}…z₀ равны 0.

9.2.1. Асинхронный двоичный счетчик

Асинхронный двоичный счетчик реализуется путем формирования последовательной цепочки триггеров, тактовый вход каждого из которых соединен с выходом Q предыдущего триггера (рис. 9.23). Чтобы счетчик работал в прямом направлении, выходы триггеров должны изменять свое состояние, когда состояние тактового импульса меняется от 1 до 0. Следовательно, здесь требуются триггеры с

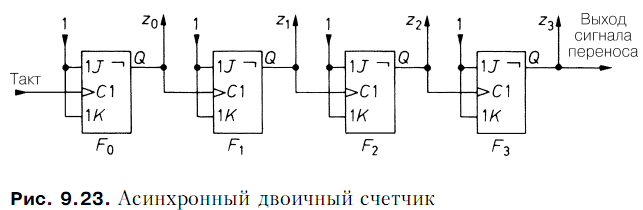
запуском по отрицательному фронту тактового импульса, например JK-триггер типа ведущий–ведомый при J = K = 1. Счетчик допускает произвольное наращивание. Так цепочка из 10 триггеров позволит подсчитать до 1023 событий.

Здесь пригодны также триггеры с запуском от положительного фронта тактового импульса, например D-триггеры, срабатывающие по одному фронту тактового

импульса. Включив их так, как показано на рис. 9.23, получим вычитающий счетчик. Для реализации прямого счетчика достаточно обращать тактовый импульс, подключая данный триггер к выходу его предшественника в цепочке.

Любой счетчик одновременно служит делителем частоты. Частота на выходе

триггера F₀ равна половине частоты входного сигнала. На выходе триггера F₁ она

составляет лишь четверть, на выходе триггера F₂ – только одну восьмую и т.д. Деление частоты очевидно из рис. 9.22.