-
Лекции «Електроніка та мікропроцесорна техніка» (Rus), ч. 1 Лекция 9,9a – Переключающие схемы
Лекция 9
9. Переключающие схемы
Под переключающей схемой понимают устройства последовательностного типа
для реализации логических функций с дополнительной способностью запоминать
отдельные состояния переменных. В отличие от комбинационных схем, переменные yj
на выходе переключаемой схемы зависят не только от входных переменных xi, но и от предыстории, определяемой состоянием триггеров.
В следующих разделах прежде всего рассматриваются устройство и принцип
действия интегральных триггеров.
9.1. Интегральные триггеры
В лекции 6 уже говорилось о простых триггерах на транзисторах. Далее мы
опишем принцип действия триггеров, ориентируясь на логические элементы. Это
позволит осознать принципы их функционирования безотносительно к используемым схемотехническим приемам.
9.1.1. Статические триггеры
Два элемента ИЛИ–НЕ с обратной связью между ними (рис. 9.1) образуют триггер с комплементарными выходами Q и Q и входами запуска (S) и сброса (R).
Если входным состояниям присвоить комплементарные значения S = 1 и R = 0,
получим:
(9.1)
и
(9.2)
Следовательно, оба выхода характеризуются истинно комплементарными состо-
яниями. Аналогично при S = 0 и R = 1 получим обратное состояние выхода, но при
R = S = 0 текущее состояние выхода не меняется. На этом основано использование
RS-триггера в качестве запоминающего элемента. При R = S = 1 оба выхода обнуля-
ются, однако их состояние оказывается неопределенным, если S и R одновременно
становятся равными нулю. Поэтому обычно состояние входов R = S = 1 считается
недопустимым. Таблица истинности (табл. 9.1) дает представление о переключении
RS-триггера.
В лекции 7 было показано, что логическое уравнение не меняется при инвертировании всех переменных и взаимной замене логических операций (+)
и (×). Воспользовавшись данным правилом,
приходим к RS-триггеру на логических
элементах И–НЕ (рис. 9.2) с той же таблицей
истинности (см. табл. 9.1). Надо лишь иметь
в виду, что входными переменными теперь
служат
и
.
Поскольку в дальнейшем предстоит часто
сталкиваться с RS-триггером на логических
элементах И–НЕ, приведем его таблицу
истинности (табл. 9.2) для входных переменных
и
.
Синхронный RS триггер
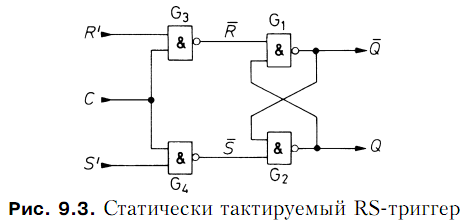
Часто используются RS-триггеры, способные реагировать на изменения состояния
входов только в течение определенных временных интервалов, задаваемых дополнительной тактовой переменной C. Такой статически тактируемый RS-триггер показан на рис. 9.3. При C = 0 имеем = = 1, и триггер сохраняет прежнее состояние. При C = 1 получается
(9.3)
В этом случае схема ведет себя как обычный RS-триггер.
Синхронный D-триггер
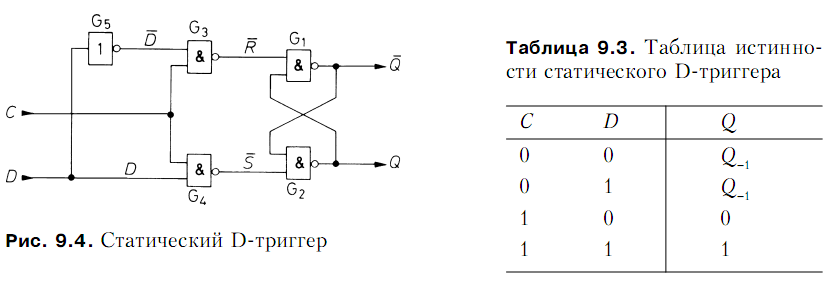
Далее рассмотрим, как можно запомнить значение логической переменной D
с помощью триггера, изображенного на рис. 9.3. Видно, что Q = S, если состояния
входов комплементарны и С = 1. Следовательно,
чтобы запомнить значение переменной
D, достаточно задать S = D и R =
.
Это делается так, как показано на рис.
9.4
посредством инвертора. У созданной таким способом ячейки памяти (триггера,
тактируемого уровнем напряжения) Q = D, пока длится такт C = 1. Это видно и
по таблице истинности (табл. 9.3). Благодаря данному свойству тактируемую
ячейку памяти называют D-триггером. Если С = 0, запоминается текущее состояние выхода.
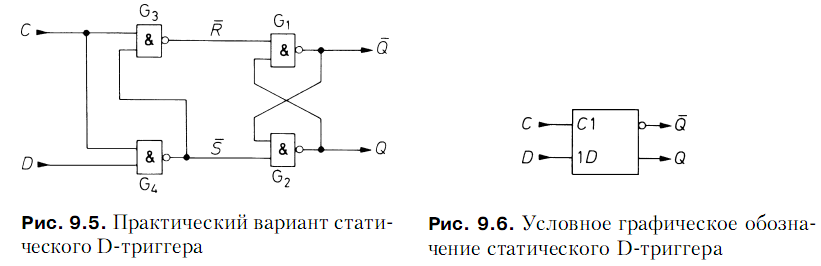
Очевидно, логический элемент И–НЕ G4 на рис. 9.4 при C = 1 действует как
инвертор для D. Это делает излишним инвертор G5 и приводит к практической
реализации D-триггера, показанного на рис. 9.5. Его условное обозначение представлено на рис. 9.6.
