1.3. Правило дифференцирования сложной функции

Вся табл. 1 производных автоматически переписывается для сложного аргумента , опираясь на теорему: Если имеет производную в точке , а функция имеет производную в точке , тогда сложная функция также имеет производную в точке , такую, что или

или .

Это означает, что , , ,

, , , , , , , , , , , , , .

Пример 3. Найти производную функций:

а) ; б) .

Решение: а) сначала дифференцируем как степень со сложным основанием: , где . Таким образом - ответ.

б) в этом случае используем формулы: , и получим .

Ответ: .

1.4. Логарифмическое дифференцирование

Если задана сложная степенно-показательная функция , то ее производная вычисляется по схеме:

1. логарифмируется заданная функция: ;

2. формально дифференцируются левая и правая части этого равенства: , или ;

3. из последнего равенства находится искомая производная: .

Пример 4. Найти производную сложной функции:

а) ; б) .

Решение: а) логарифмируем заданную функцию и формально дифференцируем это равенство:

или , .

И окончательно имеем: ;

б) для простоты вычисления вновь логарифмируем заданную функцию, используя свойства: , , . Отсюда получаем равенство , и затем дифференцируем его: . А тогда искомая производная: , где .

1.5. Производная неявной функции

Если функция задается как решение некоторого уравнения , то есть неявно, то производную находим формальным дифференцированием этого равенства.

Пример 5. Функция задана уравнением . Найти ее производную.

Решение. Формально его дифференцируем: , или , или . Отсюда получим искомую производную: . По условию , следовательно, производную можно записать иначе: .

1.6. Производные функций, заданных параметрически

Пусть зависимость функции и аргумента задана посредством параметра : , где под в механике понимается время или угол повтора, а - закон изменения абсциссы материальной точки, - закон изменения ординаты материальной точки. При таком задании функции производная вычисляется следующим образом: и характеризует абсолютную скорость материальной точки. Аналогично получаем вторую производную: , или , которая характеризует ускорение материальной точки.

Пример 6. Найти производные и заданной функции , .

Решение. Находим , . И тогда первая производная равна

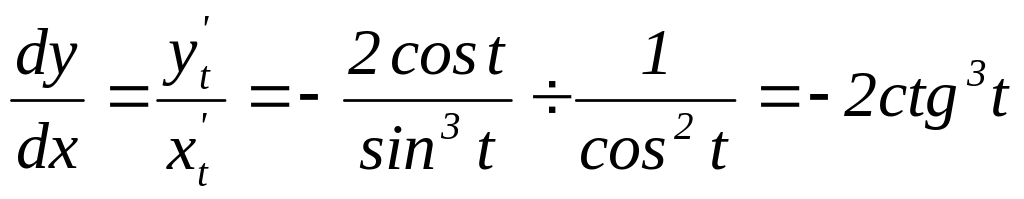. Далее получаем производную второго порядка: .

Ответ: , .

1.7. Производные высших порядков

Если функция задана явно , то ее производные находятся последовательно: .

Пример 7. Найти 4-ю производную функции .

Решение. По формуле , вычисляем . Далее , , и наконец 4-ая производная . Ответ: .

Если же исходная функция , где , , то производные вычисляются по формуле Лейбница:

, где .

Пример 8. Найти 4-ю производную функции .

Решение. По формуле Лейбница

.

Ответ: .

2. Применение производной

2.1. Производная в механике, физике и экономике

Если задан закон движения материальной точки , то отношение называют величиной средней скорости движения, а - величиной мгновенной скорости в момент времени . Следовательно, 1-я производная (или ) в механике дает скорость материальной точки.

Пример 9. Тело, выпущенное вертикально вверх, движется по закону , где - высота измеряется в метрах, а время - в секундах. Найти: а) скорость тела в начальный момент; б) скорость тела в момент соприкосновения с землей; в) наибольшую высоту подъема тела.

Решение: а) Скорость тела в момент равна производной , то есть ; в момент скорость ;

б) в момент соприкосновения с землей , то есть , откуда и (не подходит по смыслу, ибо ). Скорость тела в момент равна (минус указывает на то, что скорость тела в момент противоположна направлению начальной скорости);

в) наибольшая высота подъема будет в момент, когда скорость тела равна нулю и происходит переход от подъема к опусканию тела, то есть , откуда . Наибольшая высота подъема .

Пусть в экономике функция выражает количество произведенной продукции за время , а необходимо найти производительность труда в момент . За период времени от до количество произведенной продукции изменится от значения до значения , тогда средняя производительность труда за этот период времени . Очевидно, что производительность труда в момент можно определить как предельное значение средней производительности за период времени от до при , т.е. - производная от количества продукции .

Пример 10. Объем продукции , произведенный бригадой рабочих, может быть описан уравнением (ед.), , где - рабочее время в часах. Вычислить производительность труда, скорость и темпы ее изменения через час после начала работы и за час до её окончания.

Решение. Производительность труда выражается производной (ед./ч), а скорость и темпы изменения производительности – соответственно производной (ед./ч²) и логарифмической производной . В заданный момент времени и соответственно имеем: (ед./ч), (ед./ч²), (ед./ч) и (ед./ч), (ед./ч²), (ед./ч).

К концу работы производительность труда существенно снижается, при этом изменение знака и с “+” на “–“ свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.