6.1.1. Трубы и каналы постоянного и переменного поперечного

Рис. 6.7. Распределение относительной скорости на оси трубы в зависимости от приведенной длины X=x/(RRe) при различных значениях параметра Россби Ro.

Рис. 6.8. Кривая обратных токов в зависимости от изменения чисел Россби (Ro) и приведенной длины X. Здесь сплошная линия – расчет по настоящей модели, пунктир – данные расчета М.А. Гольдштика [16].

Рис. 6.9. Изменение коэффициента трения =c_fRe_d от приведенной длины X₃=x/(hRe_d).

Р ис. 6.10. Радиальные распределения относительной осевой скорости по длине трубы с внезапным расширением. Значки – опыт Льюиса.

Риc. 6.11. Распределение коэффициента трения Фаннингера Сf в зависимости от безразмерной длины x/D. Здесь значки – аналитическое решение.

Рис. 6.12. Распределение критерия Нуссельта Nu в зависимости от безразмерной длины x/D. Значки - опыт Петухова Б.С.[4].

Рис. 6.13 .Векторное поле скорости при ламинарном движении среды в трубе на участке в 10D.

Рис.6.14. Сравнение полей температур при движении рабочего тела с учетом переменности теплофизических свойств (верхний рисунок) и без учета переменности (нижний рисунок)

Расчеты гидродинамики и теплообмена в трубах и каналах со скачком поперечного сечения показывают, что изменение геометрии усложняет теплодинамическую картину. При высоких скоростях среднего движения в осевом направлении за уступом возникают рециркуляционные зоны (см. рис. 6.9 - 6.18). Эти области хорошо предсказываются моделью. Отличие с опытом в рис 6.10 вызвано тем, что поток, входящий в канал с диаметром D считается развитым в эксперименте, а в расчетах однороден по сечению. Однако у стенки совпадение теории и опыта удовлетворительное, вплоть до точки присоединения (линия 4). Данные показывают также, что размер рециркуляционной зоны протяженный ( ). На него влияют высота уступа h/D, Re, переменность теплофизических свойств (см. рис. 6.9 – 6.18). В точке присоединения к стенке фиксируется относительное увеличение коэффициента теплоотдачи до 2 раз. Кроме того, расчеты констатируют, что вплоть до численный алгоритм, обобщающий идеи Л.М. Симуни весьма эффективен.

6.1.3. Турбулентный режим.

Во введении мы отмечали, что расчет гидродинамики и теплообмена в инженерных системах, включающих трубопроводные участки, как правило, требуют корректного моделирования низкорейнольдсовых процессов. В таких условиях нужны подходы с детальным анализом пульсационных эффектов в гидродинамике и теплообмене, высокоточные алгоритмы. Нам представляется целесообразным познакомить студентов с возможностями и принципами использования анизотропных моделей переноса рейнольдсовых напряжений в сочетании обобщенным нами алгоритмом Л.М. Симуни. В данном разделе будут рассмотрены несколько версий моделей переноса рейнольдсовых напряжений (ПРН-моделей), предназначенных для расчета развивающихся течений вязких сред в трубах и каналах с малыми числами Рейнольдса (Сима, Ханжалика- Лаундера, Элгобаши), а также ПРН-L - модель с уравнением для интегрального масштаба турбулентных пульсаций L. Сопоставление результатов расчета с экспериментальными данными о движении жидкостей и газов будет свидетельствовать о том, что учет влияния стенки трубопровода в членах высшего порядка модели турбулентности обеспечивает приемлемую точность алгоритма решения задачи. Мы также остановимся на достоинствах и недостатках ПРН – моделей. Забегая вперед подчеркнем, что согласно результатам анализа наиболее корректными в описании внутренних течений выступают выступает модель с замыканиями отечественных ученых (ПРН-L- Глушко) и модель Элгобаши. Выбор двухпараметричекой k-L базы очень важен, так как мы имеем успешно описывать процессы в буферных областях. В тех частях, в которых любая другая модель терпит неудачу. Примером могут служить данные, изображенные на рис. 6.19, 6.20. Видно, что у стенки кинетическая энергия турбулентности (рис. 6.19), интенсивность пульсаций температуры весьма удовлетворительны.

Как известно, трубопроводный транспорт природного сырья и анализ структуры турбулентного потока в пристеночной зоне весьма сложен. Изменения в тонкой структуре при сложном движении подробно анализировались, например, в [18-20]. Данные этих работ до сих пор используются для сопоставления с результатами теоретического исследования развивающегося течения в каналах на базе утонченных моделей переноса рейнольдсовых напряжений (см. рис. 6.19, 6.20). Заметим, что прежде, чем приступить к использованию модели, необходимо убедиться в ее возможностях. В силу этого тестирование ПРН-моделей турбулентности с -базой (Ханжалика [21], Сима [22], Элгобаши [23]) это верный шаг к установлению степени доверия результатам. Кроме того, анализ литературы показывает, что такие версии весьма успешны в предсказании т гидродинамики турбулентных течений. Не будем забывать, что широко используемые в настоящее время двухпараметрические модели [типа (k-), (k-L), (k-)] применимы к практическим задачам (без их изменения на особенности процессов) в очень ограниченных случаях и требуют значительной модификации. Данный подход признан бесперспективным. Что касается алгебраических моделей рейнольдсовых напряжений (АМН-моделей), то они вряд ли окажутся универсальными из-за способа построения, опирающегося на допущения об упрощении физического явления.

В связи с этим в настоящей разделе пособия поставлены цели: адаптировать различные версии моделей замыкания рейнольдсовых напряжений к оценке развивающихся турбулентных течений в трубах; утвердиться в достоинствах представленных ПРН-моделей в расчете анизотропных пристеночных течений путем сравнения с экспериментальными данными по широкому кругу параметров; оценить замыкающие аппроксимации ПРН-моделей, значения ее численных параметров с целью развить форму модели, рекомендуемую к применению в широкой области технических приложений.

6.1.3.1. Математическая модель течения.

Общую систему определяющих уравнений, используемую для расчета развивающихся течений несжимаемой жидкости в каналах, из соображений простоты целесообразно дать в тензорной записи. В этом виде уравнения неразрывности, движения и ПРН-модель выглядят следующим образом [5]:

(1)

(2)

(3)

(4)

Здесь .

Следует остановиться на некоторых приемлемых и удачных в описании пристеночных течений в каналах подходах, используемых для замыкания уравнений рейнольдсовых напряжений, содержащих неизвестные члены высших порядков: диффузию скорости и давления ( ), перераспределения ( ) и диссипации ( ).

М1- модель Ханжалика- Лаундера [21].

Данная модель – обобщенная версия модели [24], рекомендованная для потоков с высокими числами Рейнольдса – имеет следующие представления:

(5)

(6)

(7)

(8)

где -расстояние от стенки,

Для диссипативного уравнения принято:

(9)

В настоящей пособии, основываясь на идеи [25], турбулентная диффузия в М1 упрощена и отвечает виду, представленному в (3) ( ).

М2-модель Сима [22].

С целью улучшения возможностей М1 в предлагаемой модели модифицирована постоянная в (6):

(10)

где

Член “быстрых изменений” оставлен согласно (7). Член, определяющий влияние стенки на перераспределение определяется следующим образом:

,

где

Моделирование турбулентной диффузии представляется, как и М1, согласно [21] ( ). В качестве замыкающего уравнения в М2 используется уравнение (4) вида:

(12)

где

М3-модель Элгобаши [23].

Здесь диффузия турбулентности определяется по [25] ( ). При аппроксимации особенности реального поведения нормальных напряжений учитываются видом:

(13)

-уравнение в М3 имеет вид (4) со следующими постоянными и демпфирующими функциями:

Моделирование перераспределяющего члена выполнено аналогично (5)-(8), где для принято

В случае ПРН-L- модели уравнения (1) – (3) дополняются еще уравнениями для кинетической энергии турбулентности k и интегрального масштаба турбулентных пульсаций L:

; (14)

(15)

где - касательная и нормальная составляющая P.

Значения постоянных для ПРН-L- модели турбулентности можно найти в [5].

6.1.3.2. Граничные условия и численный метод решения.

Система определяющих уравнений (1)-(4) и замыкающие соотношения (5)-(15) записываются в цилиндрической системе координат.

Краевые условия сводятся: к заданию на входе однородных профилей для осевой скорости осредненного течения, нормальных напряжений ( ), кинетической энергии и скорости диссипации ( ,где Tu-интенсивность турбулентности), другие параметры в этом случае равны нулю.

При x= (выход) принято На стенке (r=R) реализуются условия прилипания потока и отсутствия турбулентных пульсаций, а также На оси симметрии (r=0):

, V=W=0,

Численное интегрирование выполняется на неравномерных сетках. Сгущение узлов к твердым поверхностям отвечает замене переменных в исходных уравнениях:

где -параметр преобразования, обеспечивающий попадание трех- пяти узлов в область . Детали интегрирования преобразованных таким образом уравнений, выполненного с применением экономичных неявных конечно- разностных схем можно найти в [10].

6.1.3.3. Результаты анализа.

Расчеты выполнены при следующих параметрах:Re=(0.15) , D=0.0070.1м, =150D, Tu=(0.410)%, рабочее тело - воздух, вода. Сравнение с данными [1-3,11,12] по параметрам U, в развивающемся осесимметричном потоке представлено на рис.6.21-6.24. Так, на рис.6.21 изображены распределения относительной скорости по поперечному сечению в зависимости от y/R ( где y=R-r) в различных выделенных сечениях по длине от x/D канала. Линия 1 соответствует x/D=3, 2-12, 3-41. Сплошная линия относится к ПРН-L-модели [5],линия (----)-модель Элгобаши [23] M3, ( ) – модель Сима[22] М2, ( - - ) – модель Ханжалика [21] M1. Значки: - данные [26] (Re=1.6 ,D=0.01м, Tu=0.43%, воздух). На рис.6.22 даны распределения по длине трубы (x/D) в различных точках по радиальной координате (y/R). Так, линии 1 отвечают y/R =1, 2-0.3, 3-0.15, 4-0.05. Значки – эксперименты [27] (Re=400000, Tu=0.43%, обозначения те же, что и на рис.6.21). Из рис. 6.21, 6.22 видно, что результаты теории неплохо согласуются с экспериментом. Отличие расчетных данных, полученных по различным моделям незначительно. Это неудивительно, т.к. все они предназначены для расчета развивающихся внутренних течений. Однако, в области 40x/D80 как у оси, так и у стенки (рис.6.22, линии 1,3,4) имеется некоторое рассогласование, связанное с большей чувствительностью (ПРН-)-моделей к возмущениям, идущим со входа и от стенки.

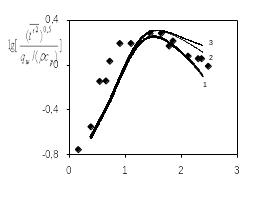
На рис.6.23 приведены профили кинетической энергии ( )10³ (где -динамическая скорость) от y/R в сечениях канала x/D=3, 12, 41 (соответственно линии 1-3). Все обозначения, включая значки, отмечающие эксперимент те же, что и на рис.6.21. Видно, что наилучшее согласие демонстрирует ПРН-L-модель (сплошная линия). Расчеты показывают, что ни одна из ПРН--моделей не предсказывает большой максимум достаточно точно, что является их общим недостатком в описании течений с малыми числами Рейнольдса. Данные о характере распределений компонентов тензора рейнольдсовых напряжений приведены на рис. 6.24.

Рис.6.24. Радиальные распределения рейнольдсовых напряжений во входной области. Здесь линия- расчет (обозначения прежние), значки – данные[18,19]: 1-x/D=20 (), 2-30 (), 3-50 (), 4-150 ().

Значки- результаты опытов [26]. (Re=30000 [19], Re=423500 [18], D=0.1м). Рисунки а)-г) отвечают распределениям в зависимости от y/R для сечений x/D=20 - линия 1, 30-2, 50-3, 150-4. Все модели удовлетворительно описывают течение в области x/D 30, однако непосредственно во входной зоне имеется рассогласование. Это связано с ограниченностью экспериментальнах данных: отсутствуют значения , k, на входе. Из рис.6.24 видно, что предпочтительнее выглядят модели ПРН-L, ПРН- (М3). Модель М1 (Ханжалика) весьма груба в определении нормальных компонент у стенки (особенно ). Модель М2 занижает большой максимум на участке стабилизированного течения на 12%, завышает максимум на 40% относительно данных [18]. Отклонение М3 в значениях порядка 8%. Использование L-уравнения [5] в ПРН-модели позволяет наиболее точно раскрыть пристеночную узкую зону течения. Из результатов следует, что отличие моделей в ядре канала незначительно. Это говорит о слабом влиянии способа аппроксимации R_ij,2 в данных моделях. У стенки М2, М3 близки, поэтому аппроксимация R_ij,w в таких моделях достаточно успешна в описании прямоточных течений. В сравнении с ПРН-L- моделью все модели с - уравнением имеют недостаток в оценке . Последняя характеристика имеет определяющее значение в приcтенном распределении кинетической энергии турбулентности.

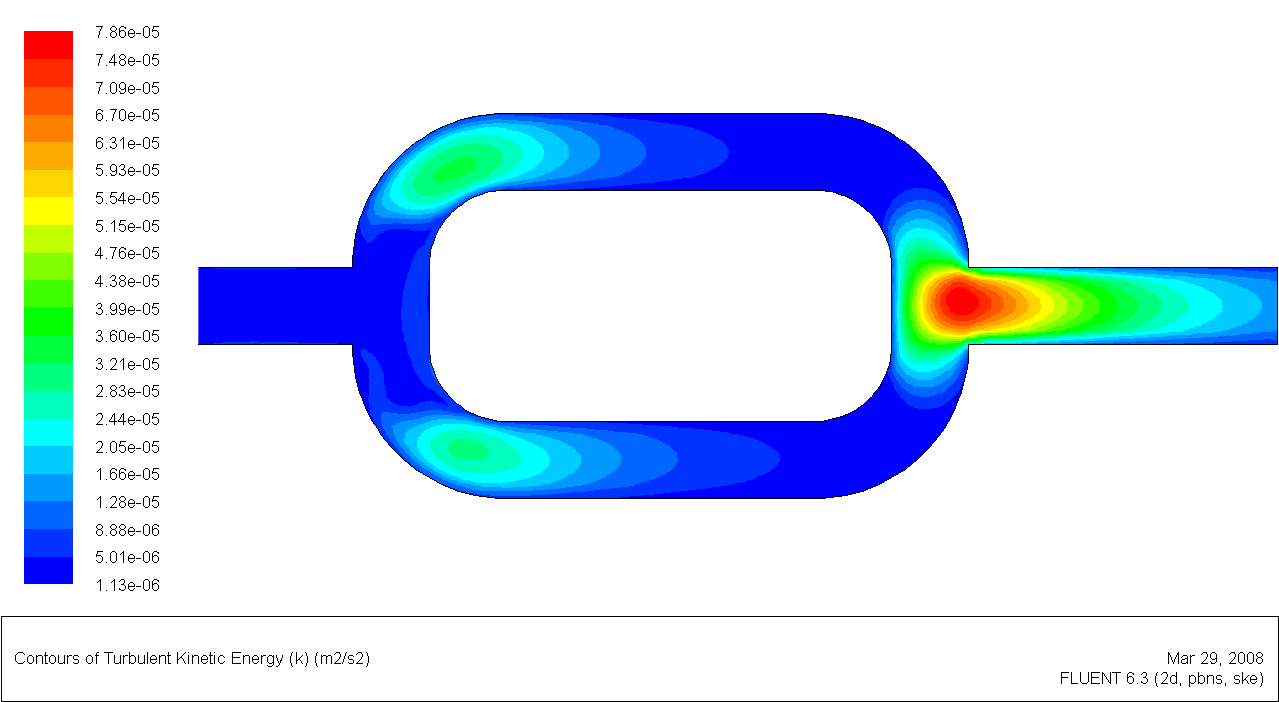
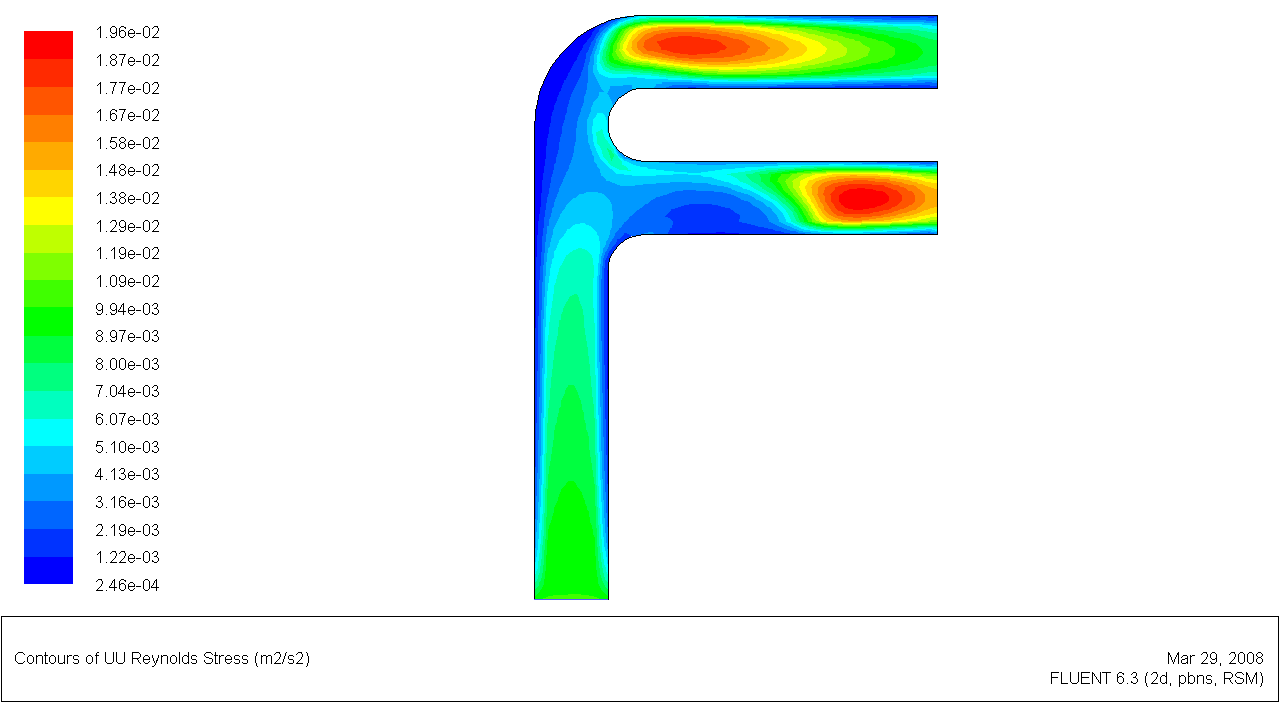
В качестве иллюстрации возможностей ПРН-L-модели (в пакете Fluent) в расчете конкретного гидродинамического течения слабосжимаемого газа в сложном канале на рис.6.25(а-е) дана карта “тонких” пульсационных параметров: поля скорости (а), турбулентной кинетической энергии (б), компонент тензора напряжений Рейнольдса (в-е).

Глава 7. заключительные замечания

Как показывает вышеизложенный материал, практические результаты работы с модулями программ, описанными моделями, методами и схемами численного расчета сложных сдвиговых течений в трубах могут быть сведены к некоторым замечаниям. Так, основные выводы по анализу гидродинамики и теплообмена при турбулентных режимах течений в трубопроводных системах, трубах и каналах с короткими и протяженными участками показывают:

• более точное описание узких пристеночных зон на базе современных алгоритмов, ПРН- моделей турбулентности должно быть связано с поиском лучших аппроксимаций членов диффузии и перераспределения. Модель Элгобаши здесь имеет преимущества в корректности учета анизотропии течения и эффектов, связанных с малыми числами Рейнольдса;

• численный алгоритм при работе со связями Элгобаши является неэкономичным. Алгоритм, построенный на базе ПРН-L-модели, требует на 50% меньше времени в сравнении с остальными при получении установившегося решения. Видно также, что особенности внутренних течений достаточно корректно можно прогнозировать на основе ПРН-L-модели, учитывающих анизотропный характер турбулентности непосредственно у стенки и позволяющих воспроизводить эффекты смещения зон экстремальной интенсивности пульсаций вглубь потока, распада энергосодержащих вихрей и их восстановление, а также элементы перемежаемости;

• описанные алгоритмы надежны и эффективны в расчете течений с особенностью границ течения, включающих неоднозначные эффекты конвективного и диффузионного взаимодействия;

• интегральный масштаб турбулентности L, уравнение интенсивности пульсаций температур весьма корректны в предсказании механизмов смещения турбулентности, ее вырождения и последующего восстановления;

• детальный анализ проблем, встречающихся при моделировании внутренних течений и теплообмена жидкости со стенками канала вполне возможен на уровне полных транспортных уравнений для тонких параметров;

• в силу взаимозависимости процессов переноса тепла, импульса по участкам труб меняющегося поперечного сечения высокие требования предъявляются эффективному численному алгоритму;

• в зависимости от высоты уступа, входных условий рабочей среды можно результативно управлять характером присоединения потока, интенсивностью механизмов переноса в рециркуляционных областях в трубопроводых системах.

Кроме того, материал позволяет отметить, что для решения уравнений механики жидкости и газа разработано большое количество конечно-разностных методов. Даже простое перечисление этих методов привело бы к длинному списку. Одни методы применяются редко и представляют исторический интерес. Другие – широко используются при исследовании многих гидродинамических течений, и с их помощью можно получить интересные результаты. Некоторые выводы и наиболее характерные результаты мы описали выше. Несмотря на большое количество схем записи конечно-разностных уравнений, можно выделить ряд закономерностей. Это позволяет провести структурный анализ схем. Последний дает возможность уменьшить объем работ при разработке программ для ПЭВМ, модифицировать программы и модели турбулентности. Чтобы убедиться в достоинствах реализованной схемы целесообразно проводить расчеты одного и того же течения с привлечением нескольких методов разностной аппроксимации уравнений переноса.

Инженер-вычислитель должен строить свою работу, опираясь на ряд правил:

1) необходимо четко сформулировать задачу и определить цели ее исследования;

2) по возможности упростить постановку без потери в точности и качестве анализируемого процесса;

3) не ожидать от модели больше, чем она может дать;

4) если возможно, использовать для сравнения имеющийся опытный материал.

список литературы

1. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений / Гл. ред. Физ.мат.лит. Наука. 1978. -592с.

2. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости/ пер с англ. М.: Энергоатомиздат, 1984. -152с.

3. Launder R.E. Heat and Mass Transport Turbulence. Topics in Applied Physics. Berlin: Springer, 1976 - 232p.

4. Петухов Б.С. Вопросы теплообмена. Избранные труды. М.: Наука, 1987. -278с.

5. Бубенчиков А.М., Харламов С.Н. Математические модели неоднородной анизотропной турбулентности во внутренних течениях. -Томск: Изд.-во ТГУ, 2001. -448с

6. Турбулентные сдвиговые течения 1/ Под ред. Ф. Дурста и др. М.: Машиностроение. 1982. -432c.

7. Глушко Г.С. Некоторые особенности турбулентных течений несжимаемой жидкости с поперечным сдвигом. // Известия АН СССР. Механика жидкости и газа. 1971. №4. с128 -136

8. Харламов С.Н и др. Математические модели течения и теплообмена во внутренних задачах динамики вязкого газа. Томск: Изд-во Том. ун-та, 1993. - 187с.

9. Роуч П. Вычислительная гидродинамика. М.: Мир, 1980. -616с.

10. Роже Пейре, Томас Д. Тейлор, Вычислительные методы в задачах механики жидкости: Пер с Англ. –Л.: Гидрометеоиздат, 1986. -350с. с ил.

11. Флетчер К. Вычислительные методы в динамике жидкостей. М.: Мир, 1990. В 2-х т.

12. Симуни Л.М. Численное решение задачи при неизотермическом движении вязкой жидкости в плоской трубе// Инженерно – физический журнал 1966. Т10. №1, с. 86-91.

13. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х т.: Пер. с англ. – М.: Мир, 1990.

14. Pfenninger W. Futher laminar flow experiments in a 40-foot long two- inch diameter tube/ Northrop Aircraft, Hawthorne, CA, Rept. AM-133, 1951.

15. Шнайдерман М.Ф., Ершов А.И. О влиянии закрутки потока на распределение скоростей и температур в круглой трубе // Инженерно–физический журнал. 1975. Т. 28. № 4. C. 630 - 635.

16. Гольдштик М.А. Приближенное решение задачи о ламинарном закрученном потоке в круглой трубе// Инженерно - физический журнал. 1959. T. 2. №3. C. 100-105.

17. Lewis J.P., Pletcher R.H. Limitation of the boundary-layer equations for predicting laminar symmetric sudden expansion flows // AIAA Paper. 1986. №1131. P. 1-8.

18. Laufer J. The structure of Turbulence in Fully Developed Pipe Flow // NACA. -1954. Rep. 1174. P. 1-18

19. Веске Д.Р., Стуров Г.Е. Экспериментальное исследование турбулентного закрученного потока в цилиндрической трубе// Изв. СО АН СССР. Сер. техн. н. -1972. -Вып.3. №13. -C.3-7.

20. Richman J.W., Azad R.S. Developing Turbulent Flow in Smooth Pipes// Appl. Sci. Res. -1973. -V.28. -P.419-426.

21. Hanjalic K., Launder B.E. Contribution towards a Reynolds-Stress Closure for Low-Reynolds-Number Turbulence// Journal of Fluid Mechanics. -1976. -V.74. -P.593-610.

22. Сима Н. Модель напряжений Рейнольдса для течения в пристеночных областях с низкими числами Рейнольдса// Теоретические. основы инженерных расчетов. -1988. -№4. -C.241-251.

23. Prudhomme M., Elghobashi S. Prediction of Wall-Bounded Turbulent Flows with an Improved Version of a Reynolds-Stress Model // Proceedings 4^th Symposium on Turbulent Shear Flows, Karlsruhe. -1987. -P. 1.7-1.12

24. Launder B.E., Reece G.J., Rodi W. Progress in the Development of a Reynolds-Stress Turbulence Closure// Journal of Fluid Mechanics. -1975. -V.68. -P.573-566.

25. Daly B.J., Harlow F.H. Transport Equations of Turbulence// Physics of Fluids. -1970. -V. 13. -P.2634-2649.

26. Grutzner H. Uber einige Ergebnisse der Untersuchung einer turbulenten Rohreinlaufstromung bei ungestrorter und gestorter Zustrromung. Beitrage zur theoretischen und experuncntellen Untersuchung der Turbulenz. Herausgeg.V.M.Hoffmeister. Akademic- Verlag Berlin. 1976.

27. Барбин, Джоунс. Турбулентное течение на начальном участке гладкой трубы// Техническая механика. -1963. -№1. -C.34-41.