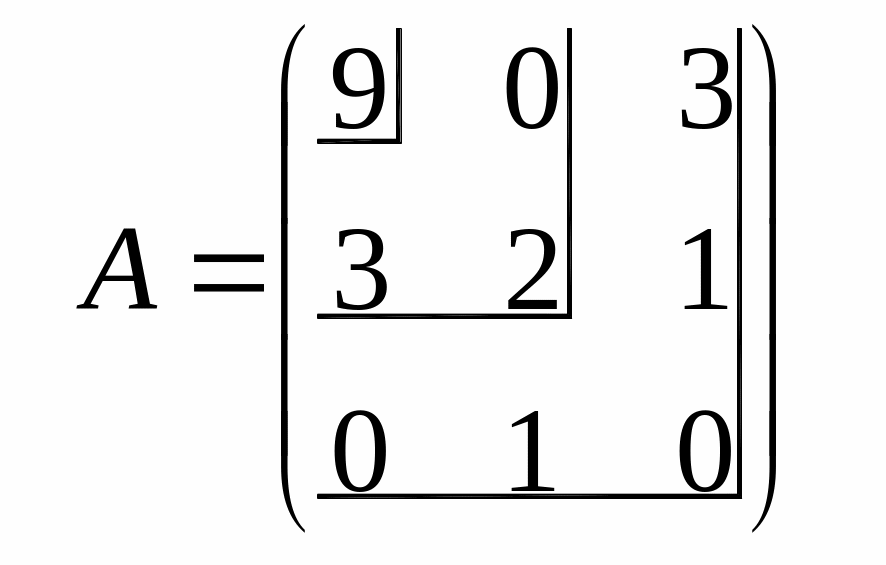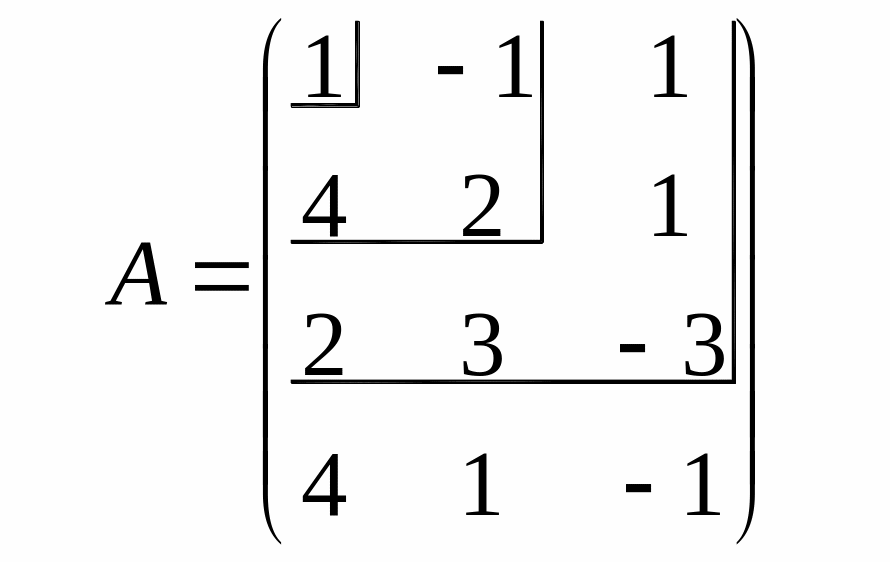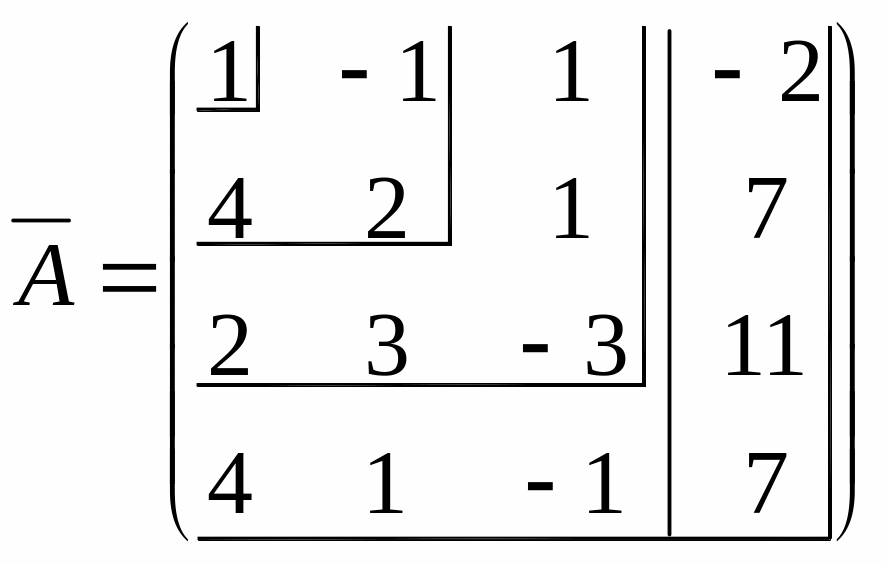7. Метод Гаусса

Для систем произвольного вида

, где

(16)

(прямоугольных), где число уравнений не совпадает с числом неизвестных, применяется общий метод последовательного исключения (МПИ) неизвестных, основанный на элементарных преобразованиях типа:

1. умножение некоторого уравнения системы на отличное от нуля число;

2. прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число, отличное от нуля;

3. перестановка местами двух уравнений системы.

Такие преобразования системы не изменяют множество ее решений и называются преобразованиями типа Гаусса. Заметим, что, выполняя преобразования 1–3 над уравнениями системы, соответствующие элементарные преобразования производятся над строками расширенной матрицы системы:

.

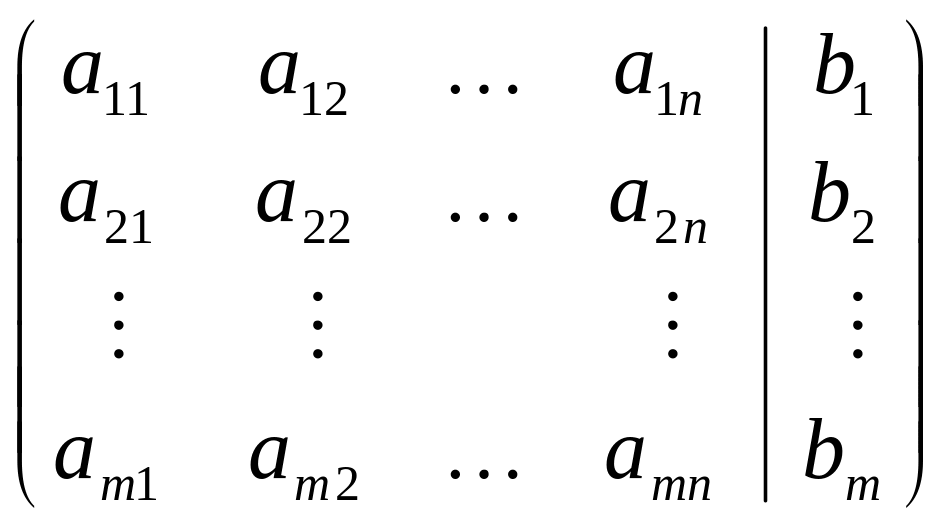Поэтому на практике экономичней проводить МПИ в матричной форме. После конечного числа шагов элементарных преобразований приходим к матрицам вида:

а)

или

б)

В случае а) система примет треугольную форму и будет иметь единственное решение, а в случае б) система примет трапециевидную форму и будет иметь множество решений.

Заметим, что если на некотором шаге появится строка , , то система будет несовместной, т.е. не будет иметь решений.

Нахождение неизвестных из преобразованной (треугольной или трапецевидной) системы идет снизу вверх и называется обратным ходом в методе Гаусса.

8. Метод Жордановых исключений

В основе метода Жордановых исключений лежат элементарные преобразования типа Гаусса, с помощью которых приводим матрицу системы к единичной . Тогда расширенная матрица СЛАУ

примет вид:

.

Автоматически получим решение СЛАУ: (см. пример 11).

При решении СЛАУ методом Жордановых исключений удобно расширенную матрицу системы записывать в виде следующей таблицы:

9. Ранг матрицы. Теорема Кронекера–Капелли

Наивысший порядок отличных от нуля миноров матрицы называется рангом этой матрицы и обозначается . Для вычисления ранга матрицы применяем метод окаймляющих миноров.

Например, задана матрица

Находим ее окаймляющие миноры:

; ; .

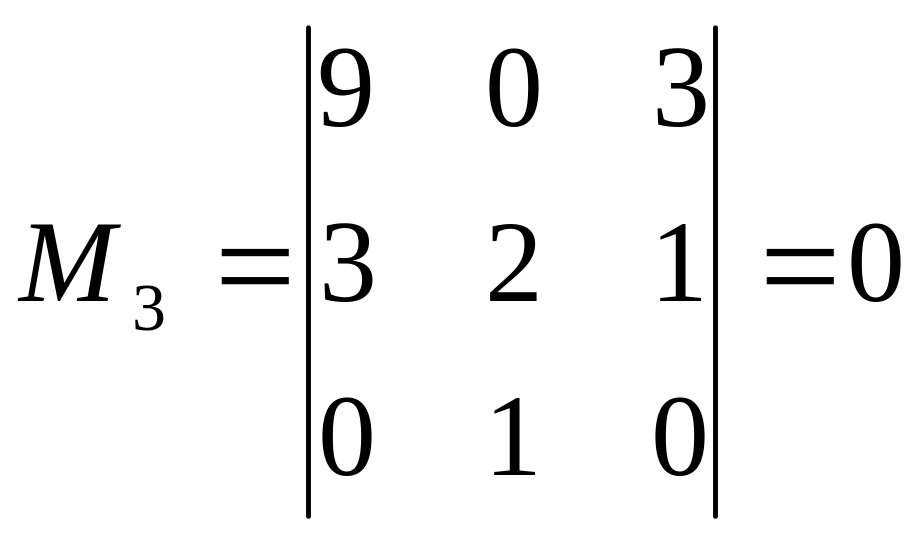Окаймляющий минор 3-го порядка равен нулю, следовательно ранг равен порядку предыдущего минора , т. е. .

Замечание. Минор порядка , содержащий в себе минор порядка , называется окаймляющим минором . Если у матрицы найдется минор , а все окаймляющие его миноры , то .

Рассмотрим произвольную систему вида (16)

Основная матрица этой системы , а расширенная , где _, . Система (16) будет совместной (т.е. будет иметь решение) тогда и только тогда, когда ранг матрицы системы совпадает с рангом расширенной матрицы этой системы, т.е.

.

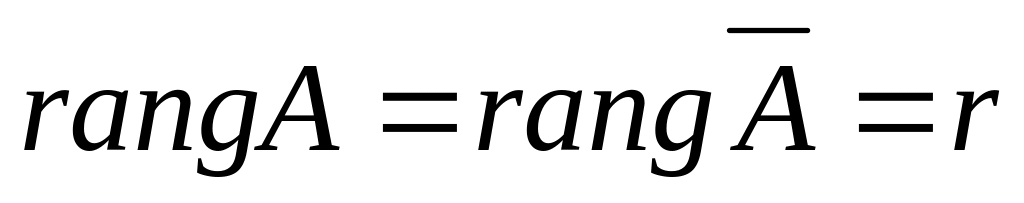Это и есть теорема Кронекера–Капелли.

Для ранга системы возможны два случая:

1. если общий ранг равен числу неизвестных 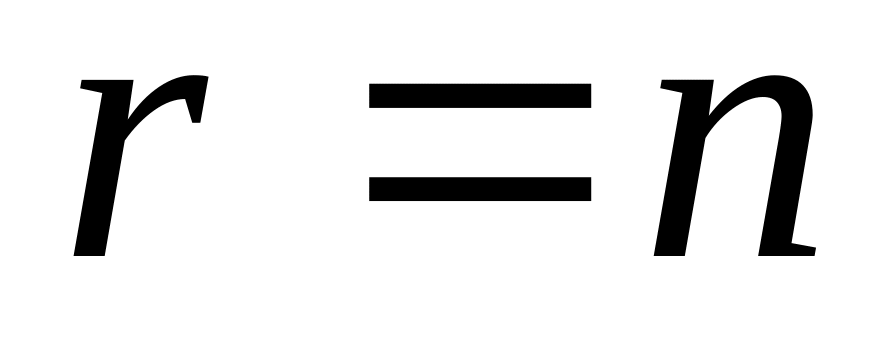, то система (16) будет иметь единственное решение;

2. если , то система (16) будет иметь бесконечное число решений.

Если же , то система (16) несовместна, т.е. не имеет решений.

Пример 11

Выяснить совместность системы и найти ее решение.

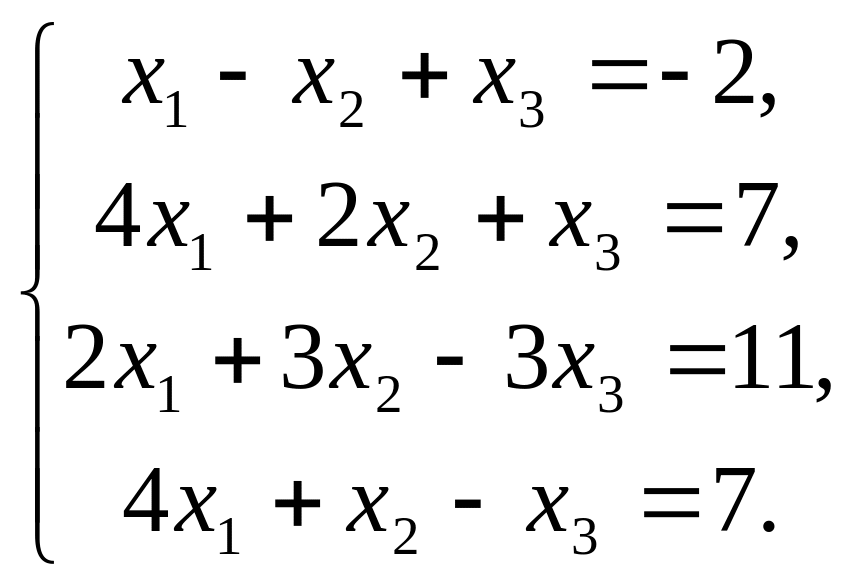
Решение

Система является переопределенной: число уравнений больше числа неизвестных . Запишем основную и расширенную матрицы системы:

и

Методом окаймляющих миноров найдем ранги этих матриц:

, , .

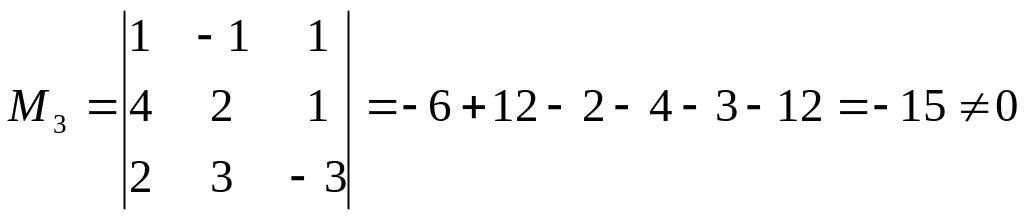Так как основная матрица не имеет минора 4-го порядка, то ее ранг равен 3, т.е. .

Для расширенной матрицы считаем окаймляющий минор:

.

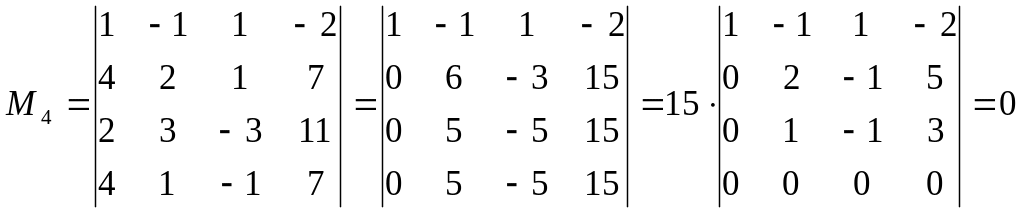Следовательно, ранг расширенной матрицы равен 3, т.е. . Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к. .

Найдем это решение методом Жордановых исключений:

+ ~ ~

~ + ~ – + ~ ~

~

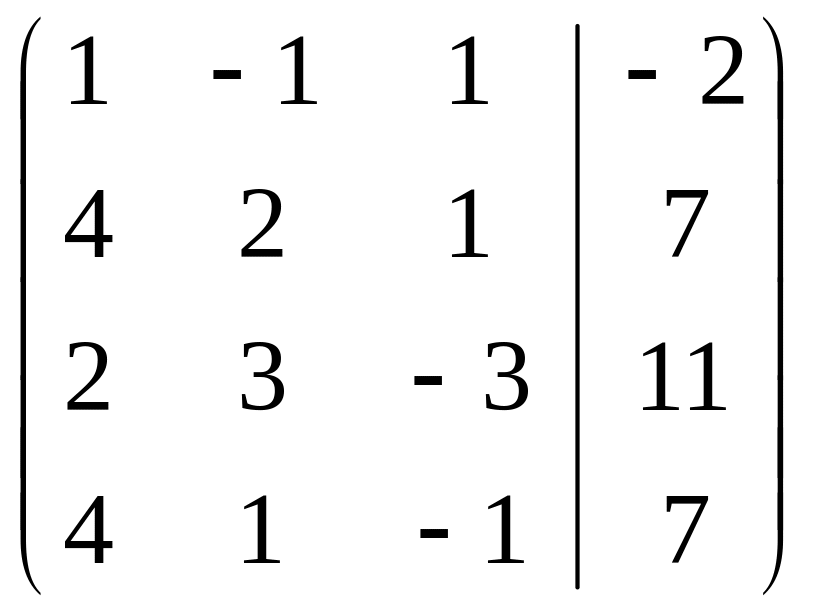
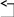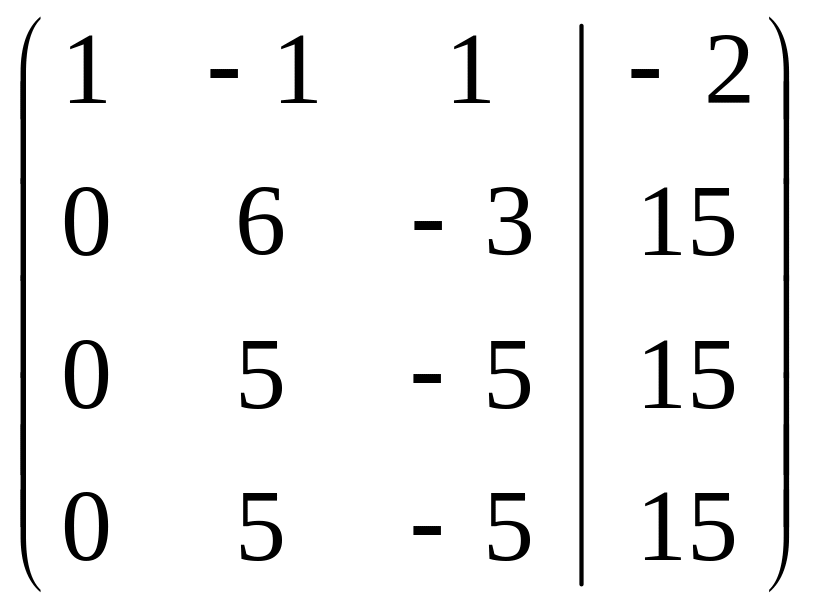
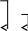
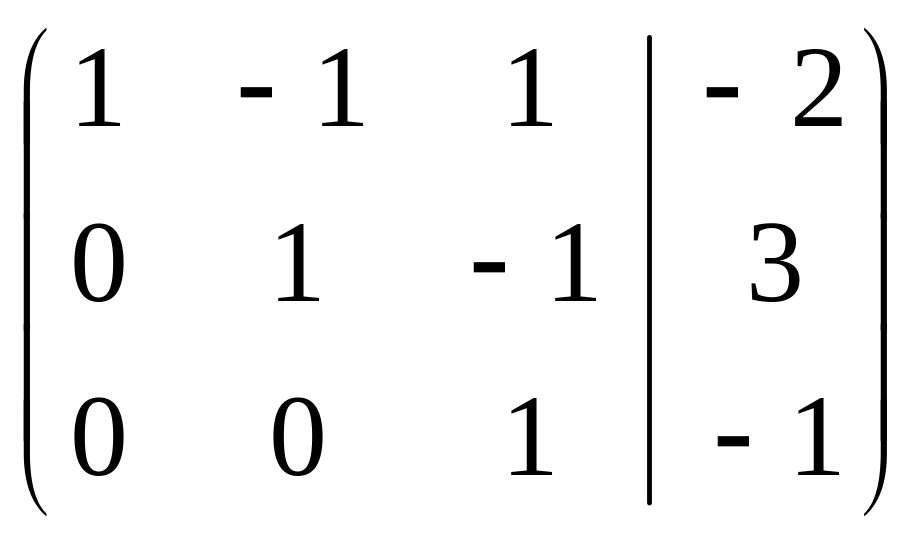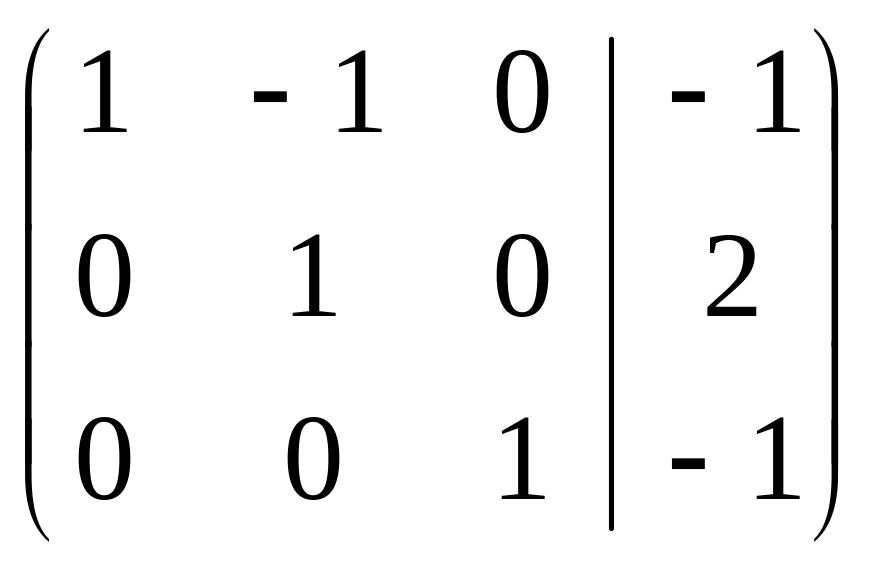
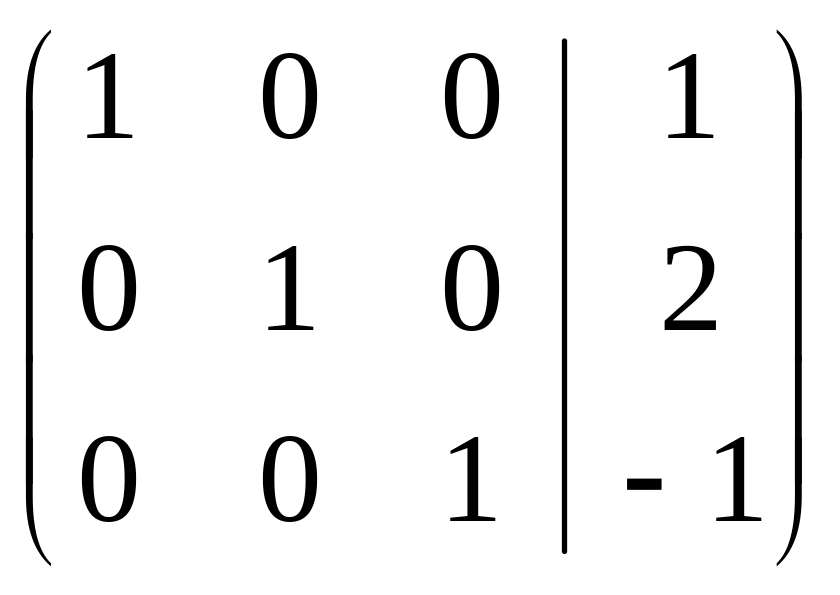
Ответ: система имеет единственное решение .
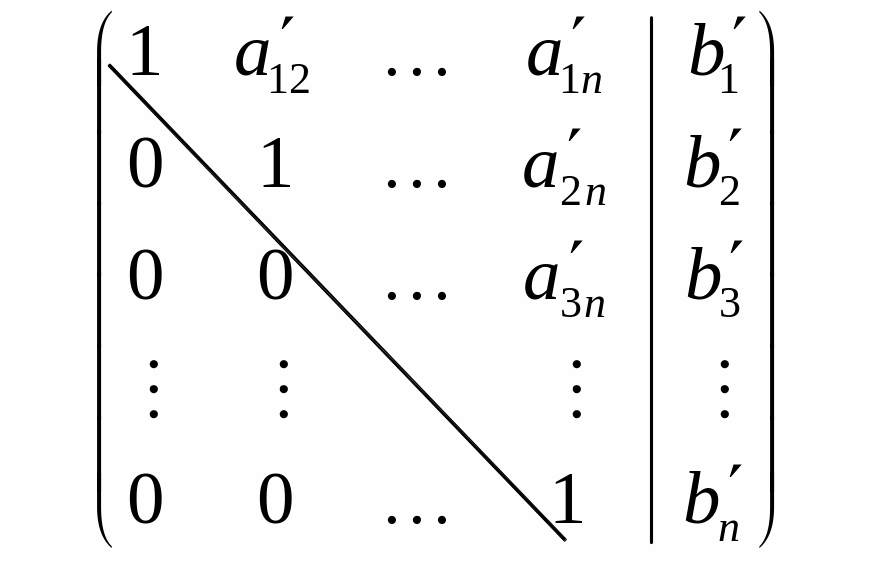
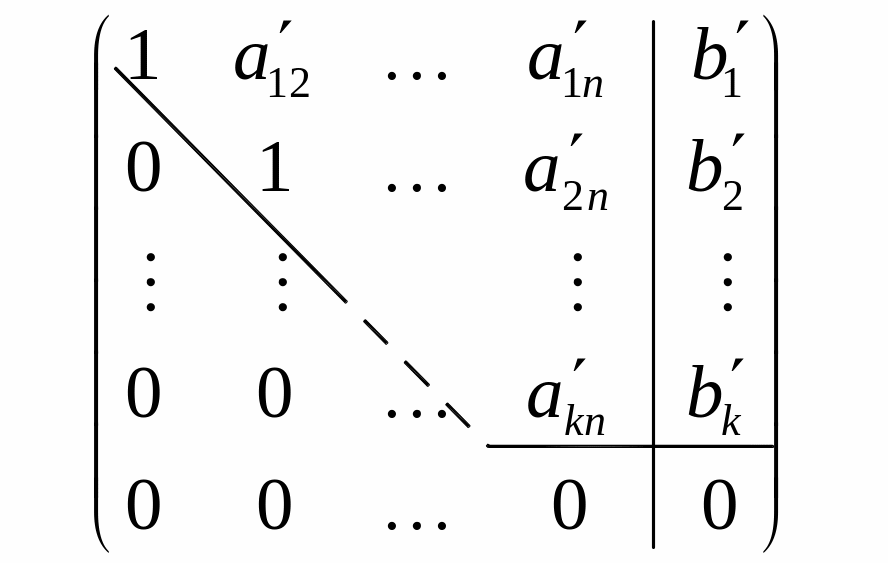
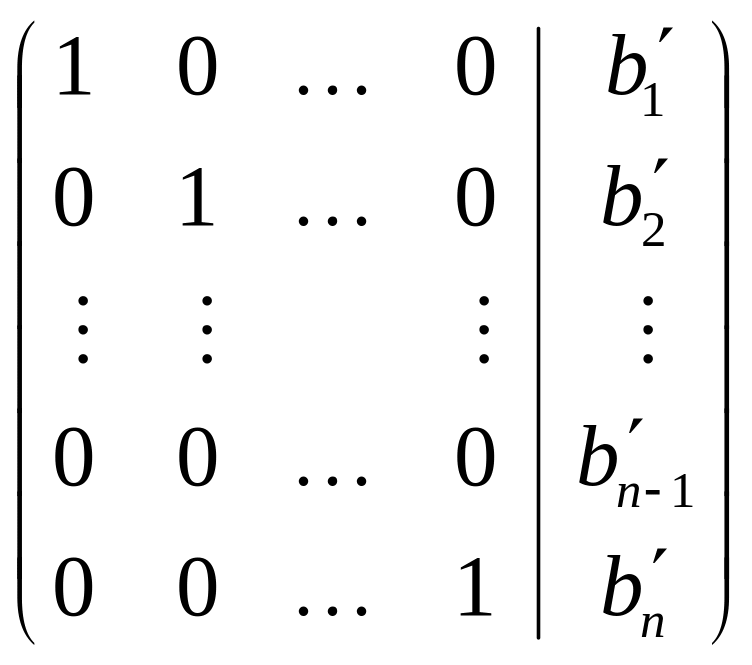