Лабораторная работа № 1

Тема: Игровые алгоритмы

1. Цель работы

Освоить приемы, методы и требования, используемые при разработке игровых алгоритмов.

2. Теоретическая часть

Дискуссии о «разумном» поведении компьютеров начались задолго до появления реальных вычислительных машин. Многие согласятся, что высокое мастерство в какой-либо интеллектуальной игре, не поддающееся полному анализу, должно свидетельствовать о незаурядных умственных способностях игрока. Если компьютер к тому же обучаем, то отрицать его интеллект еще труднее. Говоря о машинной игре, чаще всего имеют в виду шахматы, однако даже самые лучшие программы оказываются на уровне весьма посредственных шахматистов. Но в других играх можно достичь большего успеха.

Для выполнения данной работы предлагается самостоятельно выбрать любую из ниже описанных задач. Общим требованием к результатам работы является наличие сведений о правилах игры и художественные эффекты при оформлении интерфейса пользователя.

Жизнь диктует свои законы,

или…

клеточные автоматы и машинная графика

Жизнь — это многоклеточное сообщество, населяющее пустыни Флатландии. Пустыня представляет собой квадратную решетку, каждая ячейка которой вмещает одну клетку Жизни. Мерой течения времени служит смена поколений Жизни, приносящая в колонию клеток смерть и рождение.

Чтоб проследить за историей развития колонии, разместим в пустыне клетки Жизни в их начальном положении. Смена поколений будет происходить по следующим правилам.

Соседями клетки считаются все клетки, находящиеся в восьми ячейках, расположенных рядом с данной по горизонтали, вертикали или диагонали.

Если у некоторой клетки меньше двух соседей, она погибает от одиночества. Если клетка имеет больше трех соседей, она погибает от тесноты.

Если рядом с пустой ячейкой окажется ровно три соседние клетки Жизни, то в этой ячейке рождается новая клетка.

Гибель и рождение происходят в момент смены поколений.

Таким образом, гибнущая клетка может способствовать рождению новой, но рождающаяся клетка не может воскресить гибнущую и гибель одной клетки, уменьшив локальную плотность населения, не может предотвратить гибель другой.

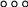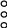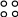Так, например, колония превращается в следующем поколении в , а колония никогда не меняется.

Хотя этого и не видно из примеров, некоторые колонии разрастаются невероятным образом при весьма скромных начальных размерах. Есть другие колонии, которые медленно перемещаются по пустыне, переходя на все новые и новые территории. Ваша программа должна обрабатывать большие колонии без чрезмерной траты памяти или времени. Многократный просмотр большого массива для построения следующих поколений – это банальный подход; здесь программистская задача состоит в выборе более экономичных структур данных и алгоритмов. Вам, возможно, захочется испытать какой-либо метод, отслеживающий только занятые квадраты. Растущая или движущаяся колония может выйти из поля зрения, если его положение и границы зафиксированы, поэтому, вероятно, понадобится еще и метод вывода, перемещающий нашу точку зрения вслед за изменениями колонии. Один из способов сокращения памяти, требуемой для запоминания позиций, состоит в том, чтобы хранить позицию в виде массива битов, отводя для каждой клетки один бит (а не слово памяти). Как это ни странно, такой способ позволяет также получить выигрыш во времени, если воспользоваться командами поразрядных логических операций над векторами битов. Если обозначить через р исходную позицию, через p1, р2, ..., р8 позиции, сдвинутые на одну клетку в направлении всех соседей клетки, и через r —новую позицию, то каждый бит г будет однозначно определяться битами с тем же номером в позициях p1, р2, ..., р8, т. е. будет логической функцией от них. Всякую логическую функцию можно, как известно, записать с помощью элементарных логических операций. Задача состоит в том, чтобы выразить г через p1, р2, ..., р8 экономно, с использованием возможно меньшего числа операций.

Колония может все время расти, непрерывно меняя свое расположение, форму или число клеток. Однако чаще колония становится, в конце концов, стационарной, начиная циклически повторять один и тот же конечный набор состояний. Длина цикла называется периодом колонии. (По этому определению период мертвой и 0000000000000000000000000пустой колонии равен единице.) Постройте программу так, чтобы она выявляла стационарные колонии и сообщала о них. Можете ли вы придумать хоть какой-нибудь алгоритм, не использующий запоминания всех предыдущих поколений, который мог бы распознать любую стационарную колонию?

История колонии Жизнь зачаровывает, если ее просматривать как фильм (это одно из соображений в пользу графического терминала), но она будет еще увлекательней, если предстанет в цвете. Каждой клетке при рождении может быть приписан некоторый цвет, определяемый, возможно, ее поколением или генами, переданными ей родителями. Циклические, но при этом движущиеся колонии (а таких немало) великолепны в своем сверкающем многоцветном наряде.

Любая колония имеет преемника, но не у каждой есть предшественник. Такие изолированные колонии называются садами Эдема. Сад Эдема можно увидеть, только если поместить его на плоскость в качестве начальной конфигурации. Подумайте, как использовать вашу программу для нахождения сада Эдема.

Крисс-кросс,

или...

эвристическое составление головоломки

Многие считают кроссворды слишком трудной головоломкой, потому что отгадать слово им не под силу. Но вписывать буквы в клетки нравится. Для подобных людей существует более простая головоломка — крисс-кросс.

Каждый крисс-кросс состоит из списка слов, разбитых для удобства на группы в соответствии с длиной и упорядоченных по алфавиту внутри каждой группы, а также из схемы, в которую нужно вписать слова. Схема подчиняется тому же правилу, что и в кроссворде — в местах пересечения слова имеют общую букву, однако номера отсутствуют, поскольку слова известны заранее. Требуется лишь вписать их в нужные места Обычно в схемах крисс-кросса гораздо меньше пересечений по сравнению с кроссвордами, а не заполняемые клетки не заштриховываются, если это не приводит к путанице. Крисс-кросс всегда имеет единственное решение, в котором используются все перечисленные слова. Заметьте, что длина слова служит важным ключом к разгадке.