3.1.6 Критерий Найквиста.

Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.

Последовательность:

1) Определяется передаточная функция разомкнутой системы .

2) Определяется число правых корней m.

3) Подставляется s = j: W_(j).

4) Строится АФХ разомкнутой системы.

Для устойчивости АСР необходимо и достаточно, чтобы при увеличении  от 0 до  АФХ W_(j) m раз охватывала точку (-1; 0), где m - число правых корней разомкнутой системы.

Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.

В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W_(j) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).

НЕЛИНЕЙНЫЕ

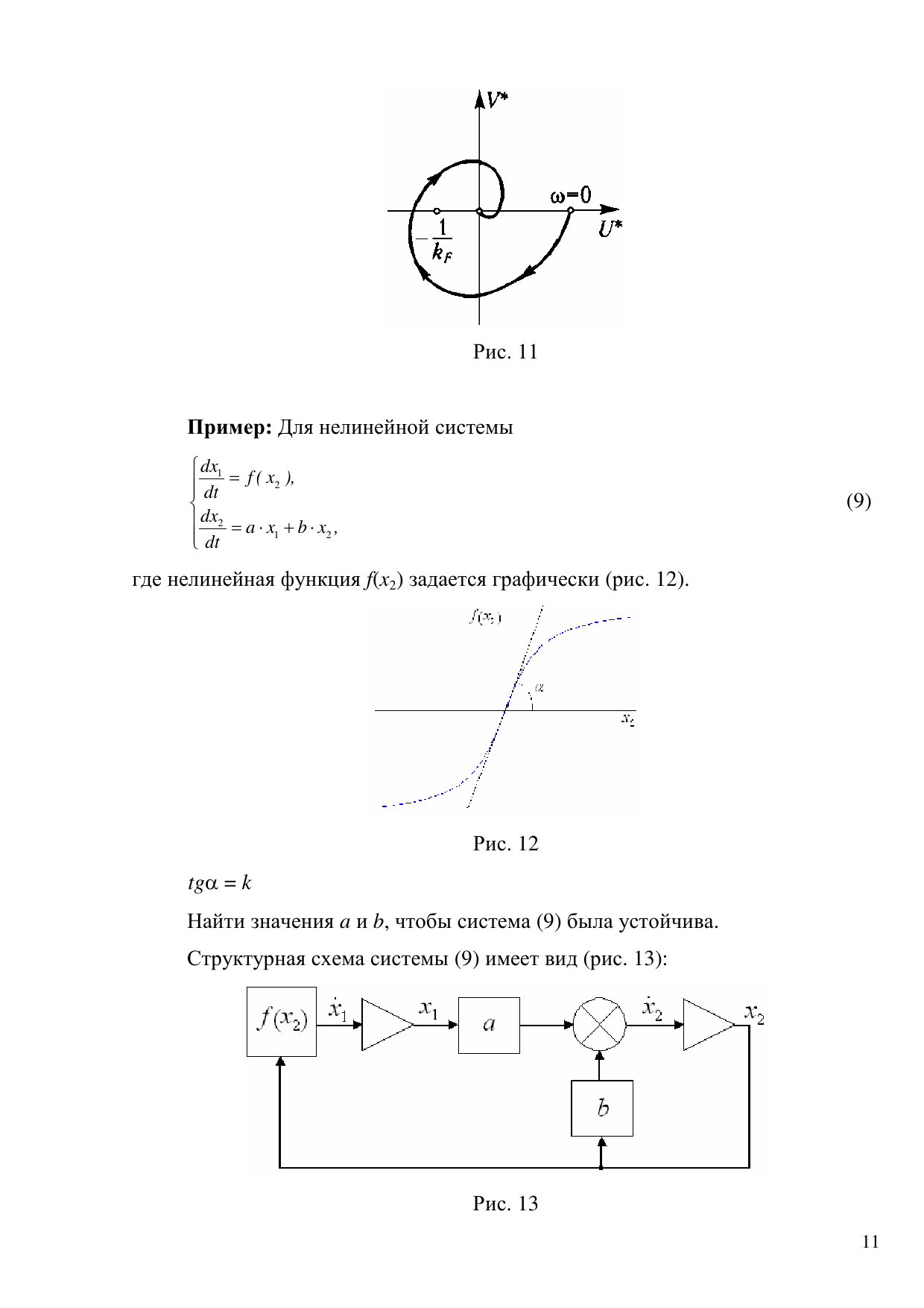
31 Расчет оптимальных настроек пи-регулятора

Оптимальная настройка регуляторов

5.1. Критерии оптимальной настройки регуляторов

Система автоматического регулирования должна удовлетворять двум основным требованиям [14]:

1. Система должна обладать достаточным запасом устойчивости.

2. В пределах запаса устойчивости не менее заданного, качество регулирования должно быть наилучшим в сформулированном смысле.

В соответствии с этим расчет оптимальной настройки регулятора состоит из определения в пространстве параметров настроек области, в которой система обладает необходимым запасом устойчивости и нахождения в этой области точки, обеспечивающей наилучшее качество регулирования.

Запас устойчивости системы может быть оценен величиной m (степень колебательности) или величиной М (показатель колебательности), которые характеризуют затухание колебательной составляющей переходного процесса и связаны однозначной зависимостью со степенью затухания Ψ:

(66)

где A₁ и А₃ – первая и третья амплитуды колебания.

Устойчивость системы автоматического регулирования полностью определяется расположением корней характеристического уравнения. Расположение же корней на комплексной плоскости можно характеризовать двумя величинами: расстоянием α наименьшего корня от мнимой оси и углом β, в который вписываются наиболее удаленные от вещественной оси комплексные корни (рис.18).

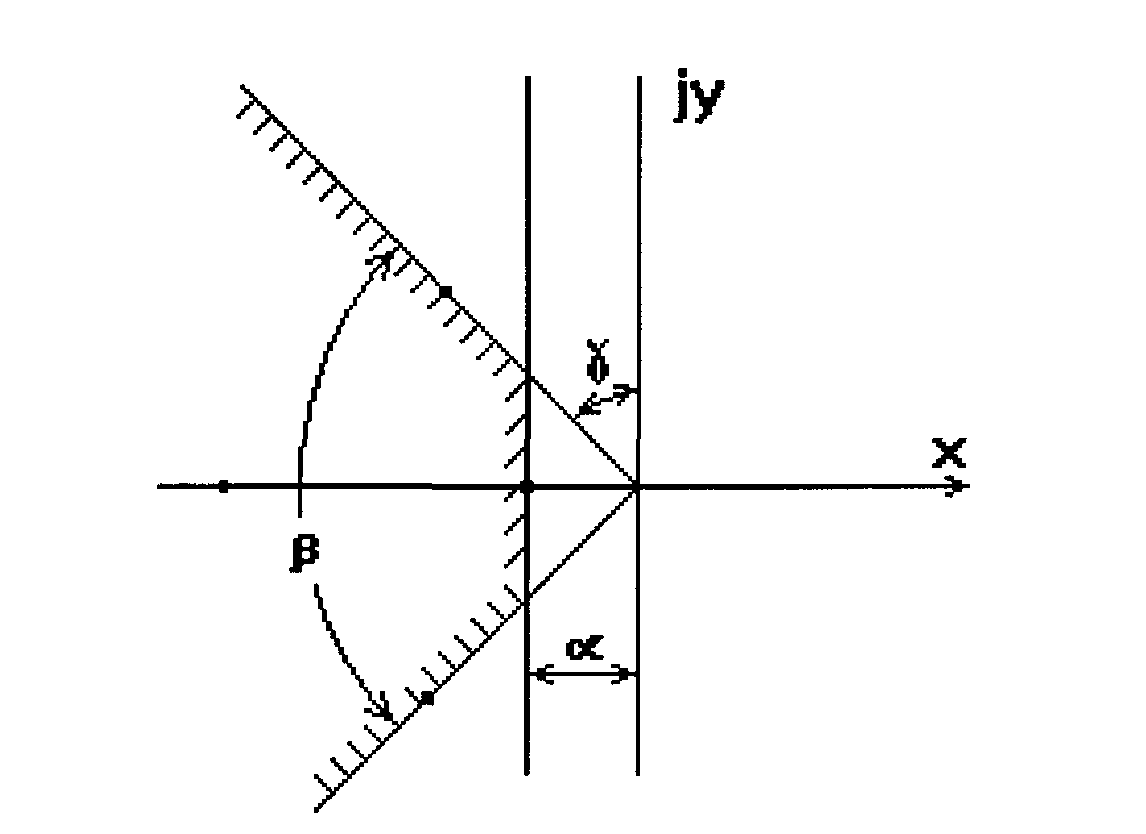
Рис.18

Величина α характеризует степень устойчивости. Чем больше α, тем быстрее затухает процесс. Величина β (или γ) характеризует колебательность системы. Чем больше β, тем больше система склонна к колебаниям. Величина m определяется как

.

(67)

Величина М определяется расстоянием максимума АЧХ замкнутой системы от критической точки (-1; j0) и определяется по формуле:

(68)

где ω_с – частота среза,

ωрез – частота, на которой АЧХ замкнутой САР максимальна.

В табл. 1 приведены некоторые соответствующие значения параметров Ψ, m и М для САР, описываемых дифференциальными уравнениями не выше второго порядка.

Таблица 1.

Ψ	0.65	0.7	0.75	0.8	0.85	0.9	0.95
m	0.167	0.192	0.221	0.262	0.318	0.366	0.398
М	3.09	2.7	2.38	2.09	1.8	1.55	1.29

Учитывая сказанное выше, для обеспечения заданного времени затухания процесса регулирования и заданной колебательности необходимо, чтобы все корни характеристического уравнения были расположены внутри заштрихованной области.

Существуют два основных способа расчета оптимальных настроек регулятора, в зависимости от того, какой параметр запаса устойчивости задан: m или М. Если задана степень колебательности т, то расчет ведется методом расширенных амплитудно - частотных характеристик. Если задан показатель колебательности М, то расчет ведется по максимуму АЧХ замкнутой системы.

5.2. Расчет запаса устойчивости методом расширенных амплитудно - частотных характеристик

Расчет системы на заданную степень колебательности производится по расширенным АФХ. [1, 17]. Расширенные АФХ W(m, jω) получаются подстановкой в выражение для передаточной функции W(p) .

Согласно обобщенному критерию Найквиста - Михайлова, переходный процесс в системе не будет содержать составляющих со степенью затухания менее заданной, если обеспечивается условие:

(69)

где Wо(m, jω) и Wp(m, jω) - расширенные АФХ объекта и регулятора.

Это уравнение является исходным при расчете границы запаса устойчивости в пространстве параметров настройки регулятора.

5.2.1. П, И, ПИ - законы регулирования

Для ПИ - регулятора расширенная АФХ имеет вид

(70)

Подставив это выражение в (69), разделив мнимую и вещественную части и решив относительно параметров Кр/Ти, Кр, получим в общем виде:

	(71)
	(72)

где Ао (m, ω) - расширенная АЧХ объекта,

Fo (m, ω) - расширенная ФЧХ объекта.

Затем строим кривую в плоскости параметров Кр/Ти, Кр.

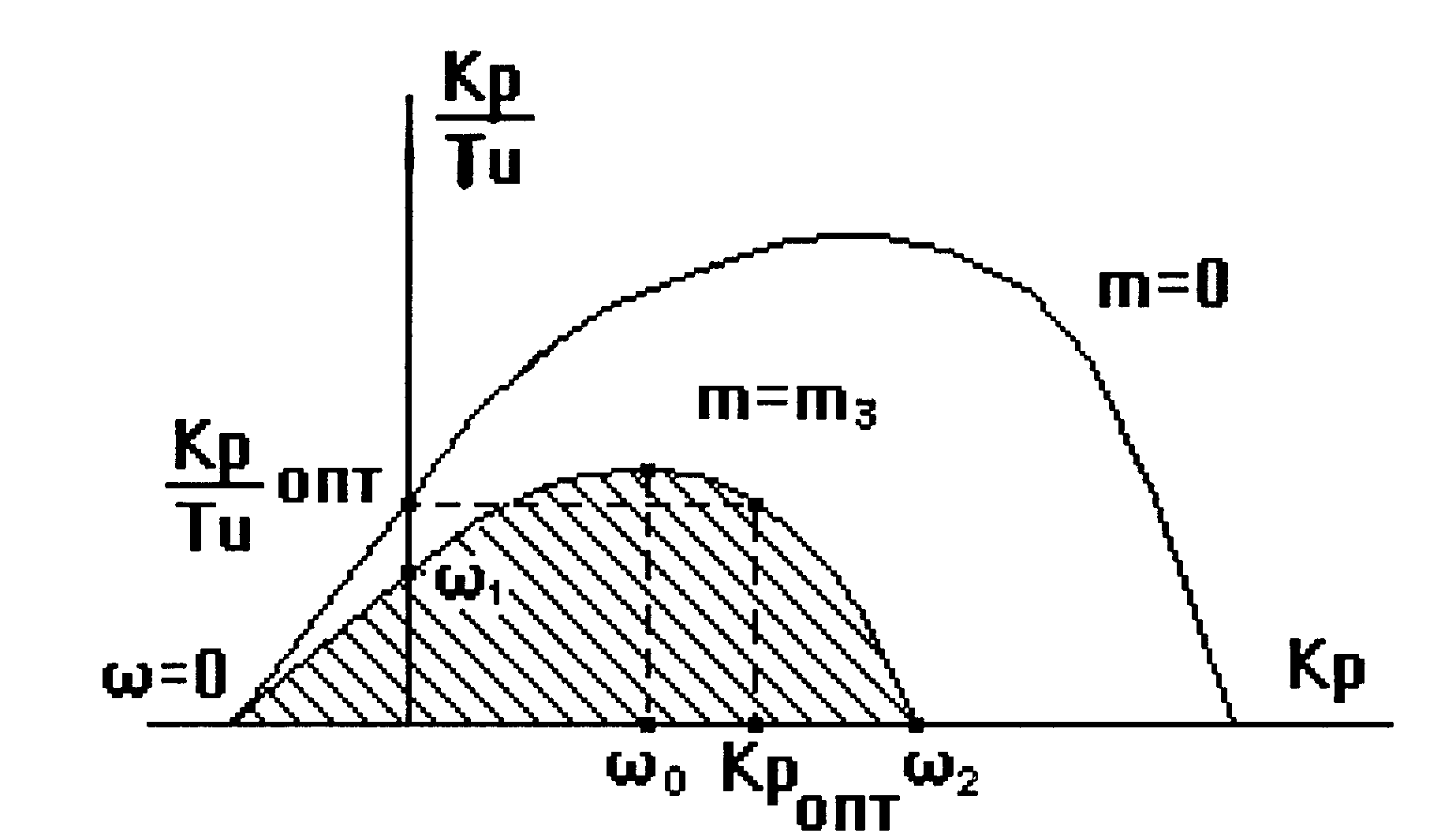
Рис.19

Область ограниченная этой кривой и прямыми Кр = 0, Кр/Ти = 0, является областью заданного запаса устойчивости. При m = 0 кривая ограничивает область устойчивости системы.

5.2.3. Расчет оптимальной настройки

После того как определена область заданного запаса устойчивости, нужно определить в этой области параметры регулятора, которые обеспечат наилучшие качественные показатели, т.е. оптимальные настроечные параметры.

Качество процессов автоматического регулирования оценивается переходными процессами при ступенчатом воздействии на входе. По переходным функциям (рис.20) можно получить основные показатели качества регулирования.

Рис.20

К основным параметрам качества относятся:

- статическая ошибка Yст, как остаточное отклонение регулируемого от заданного значения Y₀.

- перерегулирование, представляет собой максимальное отклонение регулируемой величины от заданного значения

Иногда перерегулирование задается в %, .

• время регулирования tp, определяет быстродействие системы и равно времени, в течение которого отклонение регулируемого параметра от заданного значения сделается меньше определенной величины ΔY. Иногда задается отклонение в пределах ± 5% Y₀.

• степень затухания переходного процесса - отношение разности двух соседних амплитуд одного значения к большей из них.

Оптимальные настройки регулятора обеспечивают:

• интенсивное затухание переходного процесса;

• наименьшее отклонение процесса от заданного уровня;

• минимальную продолжительность регулирования.

Эти требования тем лучше удовлетворяются, чем меньше площадь, ограниченная кривой переходного процесса (рис. 20, б). Отсюда вытекает интегральный критерий оптимальности настройки регулятора для апериодических или слабоколебательных процессов[14].

(75)

Для колебательных процессов используется в качестве оценки

(76)

Известная формула преобразования Лапласа связывает функцию времени Y(t) и ее изображение Y(p):

(77)

Отсюда следует другое известное соотношение:

.

(78)

При скачкообразном воздействии на систему:

.

(79)

Передаточная функция одноконтурной системы регулирования относительно возмущения х( t) определяется выражением:

(80)

Тогда, согласно (78), (79)

(81)

Для различных типов регуляторов, с учетом выражений для их передаточных (58), (60), (62) можно получить:

для систем с ПИ и ПИД регуляторами

(83)

где Kf и Кμ - коэффициенты передачи объекта по соответствующим каналам.

Из последних формул следует, что для минимизации линейного интегрального критерия следует стремиться к возможно большему значению коэффициента передач И - регулятора или к возможно большему отношению Кп/Ти для ПИ и ПИД – регуляторов

(84)

Отсюда следует, что для минимизации остаточной неравномерности следует установить возможно большее значение коэффициента передачи регулятора. Важным положительным свойством линейного интегрального критерия является его инвариантность относительно выбора возмущений, по каналам действия которых минимизируется критерий. Иначе говоря, выполнение условий (84) гарантирует минимизацию критерия относительно всех действующих на объект возмущений, как контролируемых, так и неконтролируемых.

На практике для ПИ - регулятора оптимальную точку настройки берут несколько правее точки, соответствующей максимуму Кр/Ти (рис.19). Примерно можно считать, что ω_р = 1.2ω₀, где ω_р - частота регулирования, а ω₀ - частота соответствующая максимальному значению настройки регулятора. Для ПИД - регулятора стремятся иметь максимальное отношение Кр/Ти при отношении времени предварения к времени изодрома близкое к Тд/Ти = 0.5.

Приближенные оценки оптимальных параметров настроек регуляторов даны в [2, 19].

При использовании квадратичного интегрального критерия (76) условие его минимизации записывается в виде [14]:

(86)

Интегральный квадратичный критерий не инвариантен относительно возмущений, действующих по различным каналам. Поэтому может сказаться, что параметры настройки, минимизирующие этот критерий при действии одного возмущения, не будут оптимальны по отношению к другим возмущениям.

Приближенные оценки оптимальных параметров настроек регуляторов даны в [2, 21].

5.3. Расчет запаса устойчивости по величине максимума АЧХ замкнутой системы

Запас устойчивости системы характеризуется степенью удаления АЧХ от точки {-1, j0} и измеряется двумя параметрами: запасом устойчивости по модулю (С) и запасом устойчивости по фазе (γ) (рис.21).

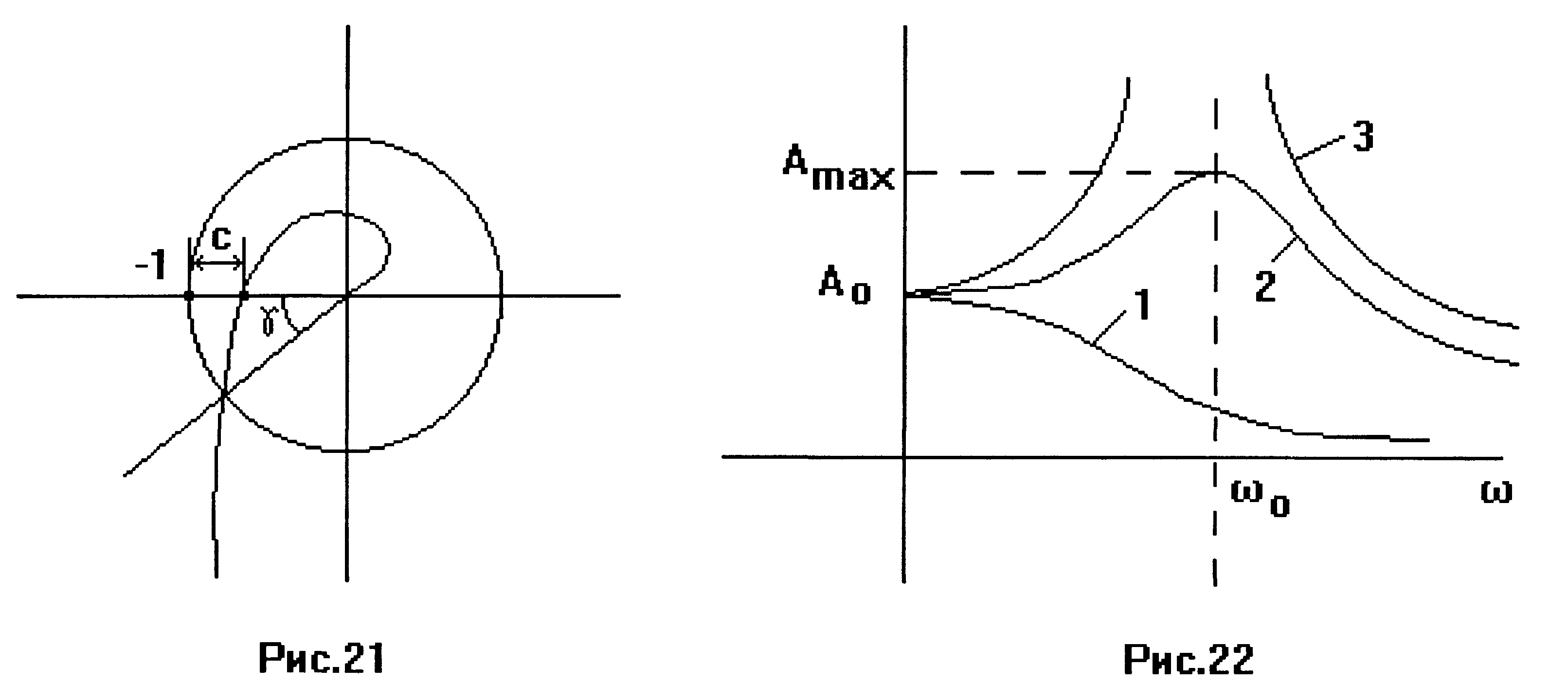
Степень удаления АФХ разомкнутой системы от точки {-1, j0} может быть определена по величине максимума АЧХ замкнутой системы [14]. Чем больший максимум имеет АЧХ замкнутой системы, тем ближе АФХ разомкнутой системы к точке {-1, j0} и, следовательно, тем меньший запас устойчивости имеет система.

На рис.22. 1 - АЧХ системы с неколебательными переходом процессом, 2 - с колебательным переходным процессом, 3 - на границе устойчивости. Колебательность М = Аmax/А₀, или (68). Кривая, удовлетворяющая условию М = const является окружностью с радиусом , а центр находится на отрицательной вещественной полуоси на расстоянии от начала координат (рис.23).

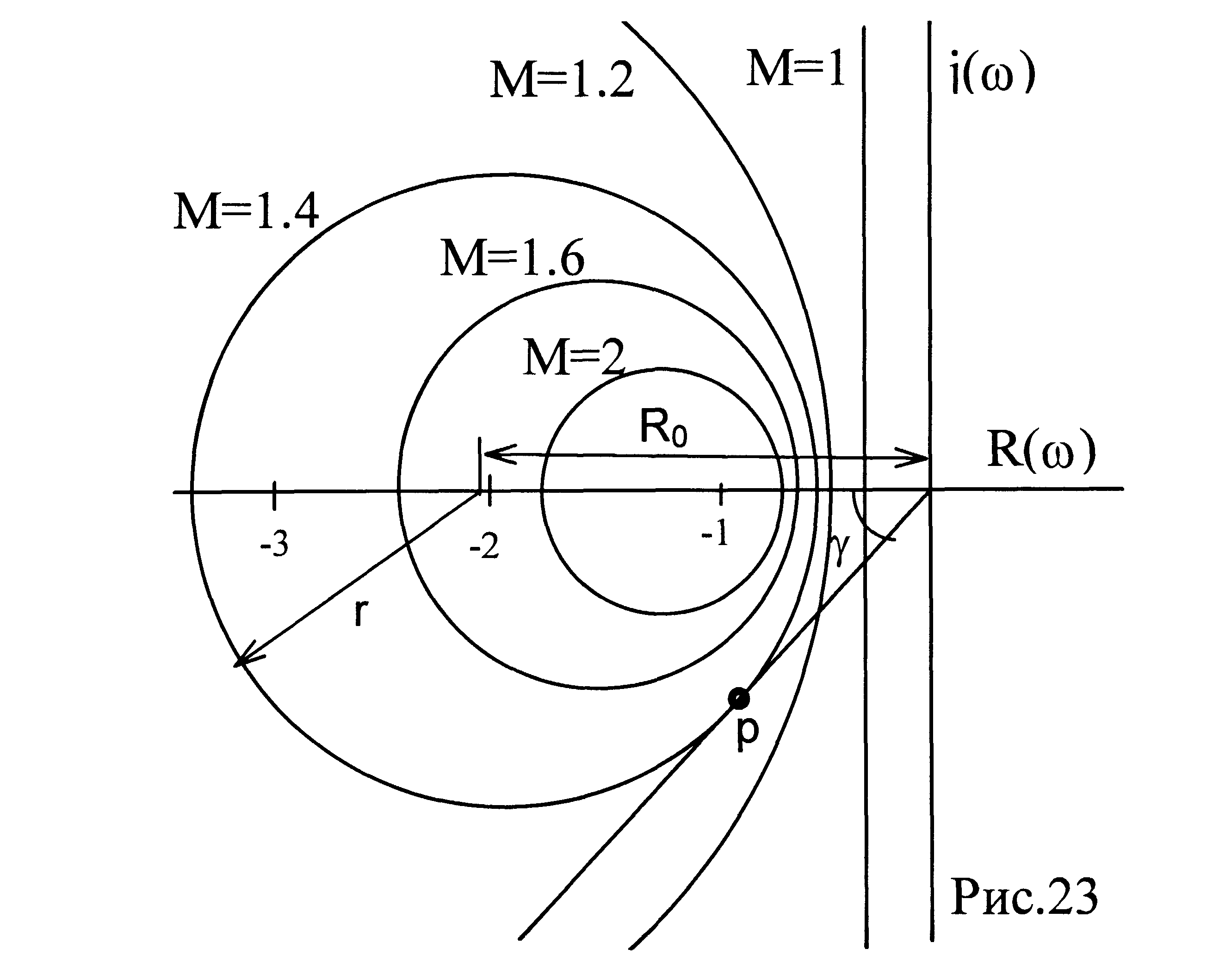
Эти окружности удовлетворяют свойствам:

• угол наклона между касательной, проведенной из начала координат к М - окружности и отрицательной действительной полуосью равен

• перпендикуляр из точки касания Р касательной и М - окружности к действительной оси пересекает ее отрицательную ветвь в точке {-1}.

На основании этих свойств М - окружностей для выбора параметров разомкнутой САР, обеспечивающих заданное значение максимума АЧХ замкнутой САР относительно управляющего воздействия, выполняют следующее:

• строят в комплексной плоскости АФХ разомкнутой системы (обычно для Кр = 1).

• проводят луч ОЕ из начала координат плоскости W(jω) под углом к отрицательной действительной полуоси.

• подбирают окружность с центром на отрицательной ветви действительной оси, касающуюся одновременно АФХ разомкнутой системы и луча ОЕ.

• Проводят перпендикуляр к действительной оси из точки касания найденной окружности и луча ОЕ и определяют координату точки пересечения перпендикуляром действительной оси: {-А}.

• рассчитывают по соотношению I = 1/А, во сколько раз нужно изменить масштаб построения, чтобы выполнить условие . На практике проводят расчет из условия обеспечения величины 2,38 > М > 1,55, что соответствует в системе второго порядка 0,221 < m < 0,368 (0,75 <у< 0,9).

Рассмотрим особенности построения АФХ систем с регуляторами различных типов.

5.3.3. АФХ системы с ПИ – регулятором

(89)

при Кр = 1.

Для получения АФХ разомкнутой системы с ПИ - регулятором при Кр = 1 и некотором Ти следует к каждому вектору характеристики объекта добавить вектор длиной ΔА = А₀/(ωТи ), повернутый на 90° по часовой стрелке (рис. 26, а).

Критическая величина Кр.кр для выбранного Ти равна обратной величине отрезка, отсекаемого характеристикой W(jω) на отрицательной вещественной полуоси (рис. 26, а).

Производя построение для различных времен изодрома Ти по изложенной методике и определив соответствующие им Кр.кр можно в плоскости параметров настроек Кр - Ти построить границу области устойчивости и определить оптимальное значение Ти (рис. 26, б).

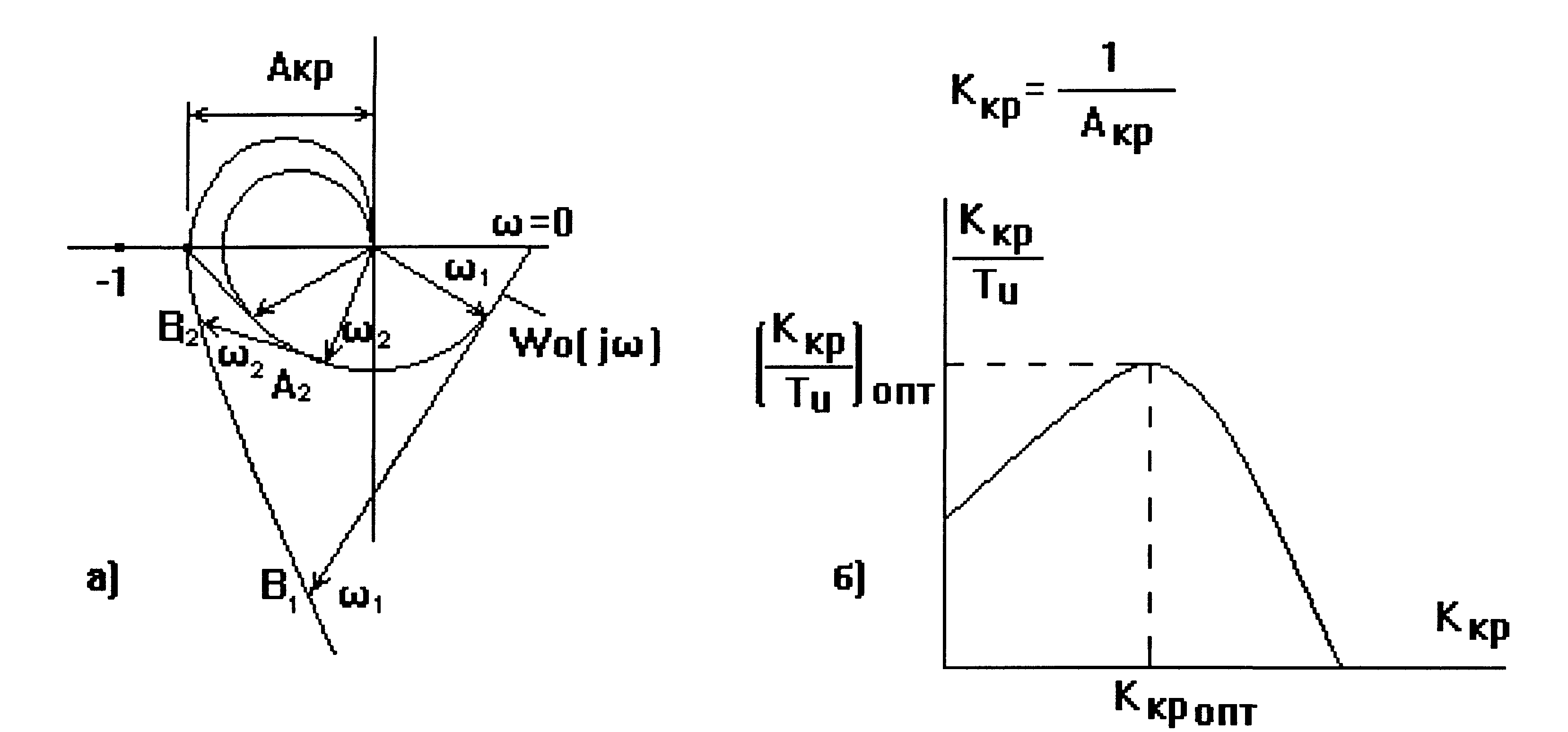
Рис.26

5.3.5. Пример расчета настройки ПИ – регулятора.

Определить параметры оптимальной настройки ПИ - регулятора температуры электропечи, обеспечивающие при запасе устойчивости М = 1.62 минимальное значение линейного интегрального критерия J.

Динамические свойства объекта по каналу регулирующего воздействия заданы вещественной и мнимой частями АФХ (табл. 2) при Ко = 84мВ, АФХ системы с ПИ - регулятором определяется уравнением

(93)

или при Кр = 1

(94)

По изложенной выше методике строим АФХ разомкнутой системы для Кр=1 и Ти=1,1.5,2,3 мин. и выполняем все дополнительные построения (рис.28).

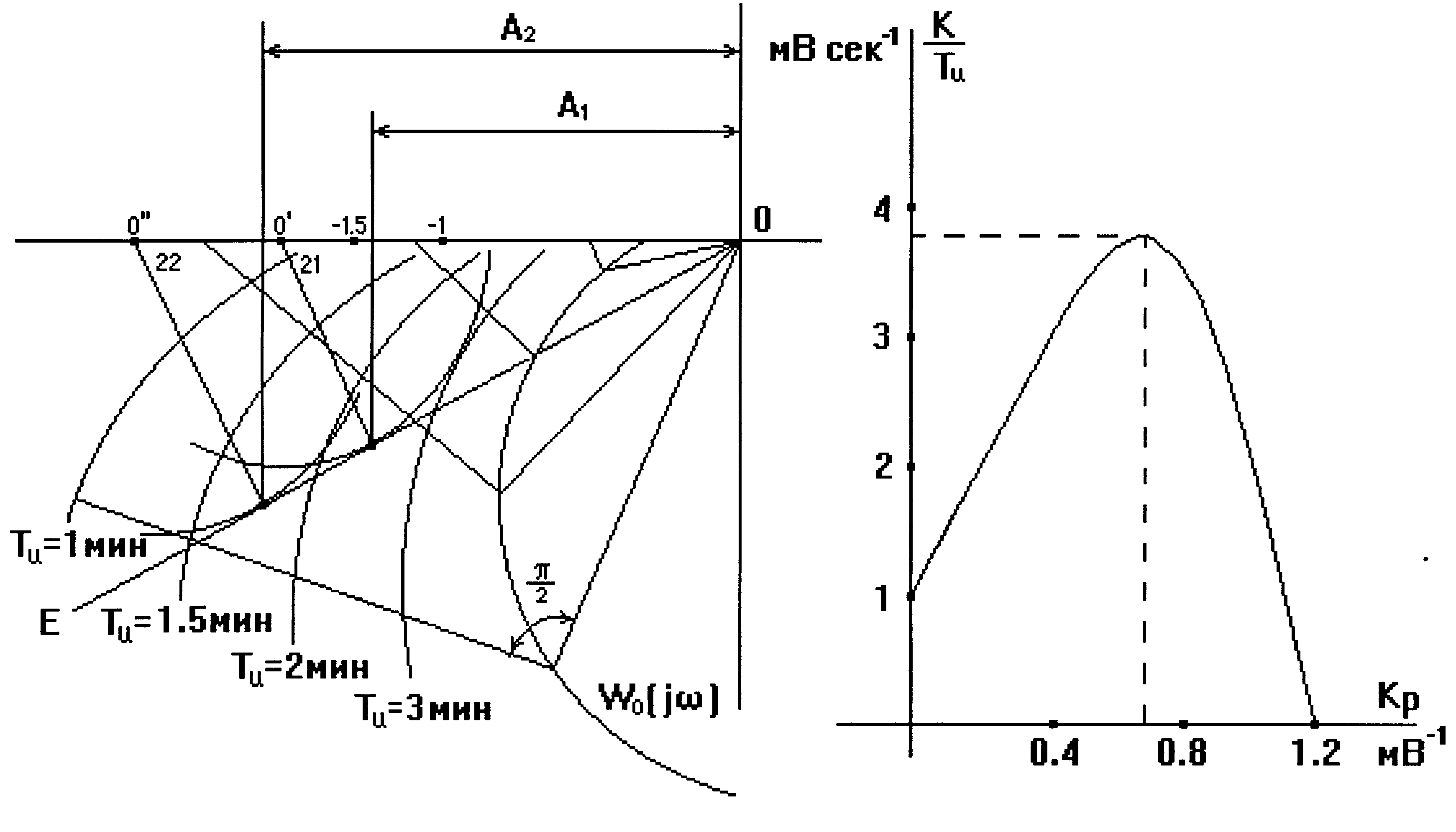
Рис.28

В результате построений получаем:

А =10.4	Ти = 3 мин
А =12.9	Ти = 2 мин
А =14.6	Ти = 1.5 мин

отсюда

Таблица 2.

ω, 1/мин	R(ω), мВ	J(ω)		ω, 1/мин	R(ω), мВ	J(ω)
0.25	42.4	-43.2		1.5	-6.6	-8.8
0.4	18.4	-32		2.0	-6.2	-5
0.75	0	-21.2		2.62	-5.1	-2.4
1.0	-4.2	-15.6		5.2	-2.08	0

Кроме того,

По этим данным строим кривую в плоскости параметров настройки регулятора (рис.28, б). Минимуму линейного интегрального критерия отвечает условие (Кр/Ти)мах. Таким образом, оптимальные настройки определяется значениями