2.6. Выполним оценку согласования статистического распределения с нормальным законом распределения, используя критерий хи-квадрат Пирсона.

Распределение случайной величины, в принципе, невозможно точно определить по результатам опытов. Полученные экспериментально оценки распределения дают возможность только строить различные гипотезы о распределении случайной величины, например, гипотезу о том, что она распределена нормально. Поэтому возникает задача проверки гипотез. Эта задача состоит в том, чтобы определить, насколько хорошо согласуется та или иная гипотеза о распределении случайной величины с полученными экспериментальными данными.

Для проверки гипотез о распределении применяются различные критерии согласия. Наиболее удобным является критерий ХИ – квадрат Пирсона. Он совершенно не зависит от распределения случайной величины, от ее размерности. Мерой согласия является величина , равная

,

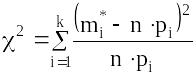где k – число разрядов гистограммы;

– вероятность попадания случайных значений в соответствующий интервал , вычисленная по теоретическому закону;

– статистическая частота попадания случайного значения в соответствующий интервал;

– число произведенных измерений.

Для случая аппроксимации статистического распределения нормальным законом вероятность попадания случайных значений величины в каждый из интервалов вычисляют с помощью формулы Муавра – Лапласа

,

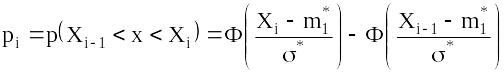где – функция Лапласа. В справочной литературе приводятся значения для различных значений . Данная информация приведена в приложении Б.

Таблица 2.6.1 – Результаты вычисления функции Лапласа

Xi	67,5	71,63	75,75	79,875	84
u	-3,9060978	-3,14	-2,37028	-1,60237	-0,8344613
Ф(u)	-0,499948	-0,5	-0,4911	-0,4452	-0,2967
Xi	88,125	92,25	96,375	100,5	104,625
u	-0,0665521	0,701357018	1,469266162	2,237175306	3,00508445
Ф(u)	-0,0259	0,258	0,4292	0,4875	0,49865
Xi	108,75	112,875	117
u	3,7729936	4,540903	4,653011
Ф(u)	0,499928	0,499997	0,499997

Таблица 2.6.2 – Результаты вычисления вероятностей по формуле Муавра – Лапласа и значения критерия

p1=	0,000968
p2=	0,00788
p3=	0,0459
p4=	0,1485
p5=	0,2708
p6=	0,2839
p7=	0,1712
p8=	0,0583
p9=	0,01115
p10=	0,001278
p11=	0,000069
p12=	0,000000

Критерий будет равен: = 21,370.

Распределение ХИ-квадрат зависит от параметра , называемого числом степеней свободы распределения, определяемого по формуле

,

где k – число независимых связей.

Примерами связей могут быть

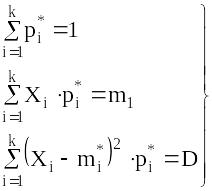, и т.д.

Первое условие должно вводиться для всех видов распределения параметров. Кроме этого, должно выполняться условие равенства теоретических и статистических моментов: начального первого порядка и центральных второго и более порядков. Для случая нормального закона распределения ограничиваются условиями равенства моментов первого и второго порядков с соответствующими теоретическими, т.е. и .

Следовательно h=3, k=12, тогда r=9

Так как в таблице для = 21,370 и r=9 значение p=0,01, данное распределение не согласуется с нормальным законом.